8.2 Розрахунок на міцність при косому згині

Для визначення небезпечних точок у даному перерізі треба знайти поло­ження нейтральної лінії. Її рівняння визначається з умови 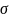(z, у)= 0, тобто

(8.3)

звідки

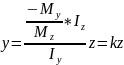(8.4)

Кут нахилу нейтральної лінії до осі z знаходиться з виразу для кутового коефіцієнта k прямої (8.4)

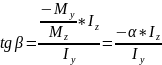(8.5)

З (8.5) видно, що на відміну від прямого згину при косому згині нейтраль­на лінія (нл.) і силова лінія (р.р.) в загальному випадку (коли 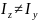) не будуть взаємно перпендикулярні (рис. 8.3). Для перевірки на міцність слід спочатку побудувати епюри згинальних моментів М_z і М_у. З цих епюр вибрати небез­печний переріз, де М_z і М_у по модулю одночасно великі. Таких перерізів мо­же бути декілька. Далі в небезпечному перерізі слід знайти небезпечні точки — це точки, які найбільш віддалені від нейтральної лінії — точки В і D (рис. 8.3). У точці В діє найбільше розтягуюче, а в точці D — найбільше стискаюче на­пруження. Умова міцності для небезпечних точок має вид

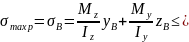
(8.6)

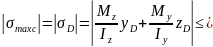
Відмітимо, що якщо поперечний переріз балки має дві осі симетрії (напри­клад, прямокутник, двотавр), то небезпечними будуть завжди кутові точки В і D (рис. 8.3). Умова міцності записується у вигляді

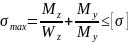(8.7) (8.7)

Для визначення прогину також використовуємо принцип незалежності дії сил і обчислюємо прогин в кожній з головних площин.

Позначимо прогин в на­прямку осі у через 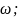а в напрямку осі г через V. Тоді диференціальні рівнян­ня прогинів у площинах хz і уz запишуться у вигляді

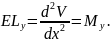; (8.8)

Інтегруючи (8.8), визначаємо О) і V.

Величина повного прогину перерізу визначається як геометрична сума прогинів і V:

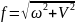(8.9)

8.3 Поза центровий розтяг або стиск стержня. Визначення нормальних напружень

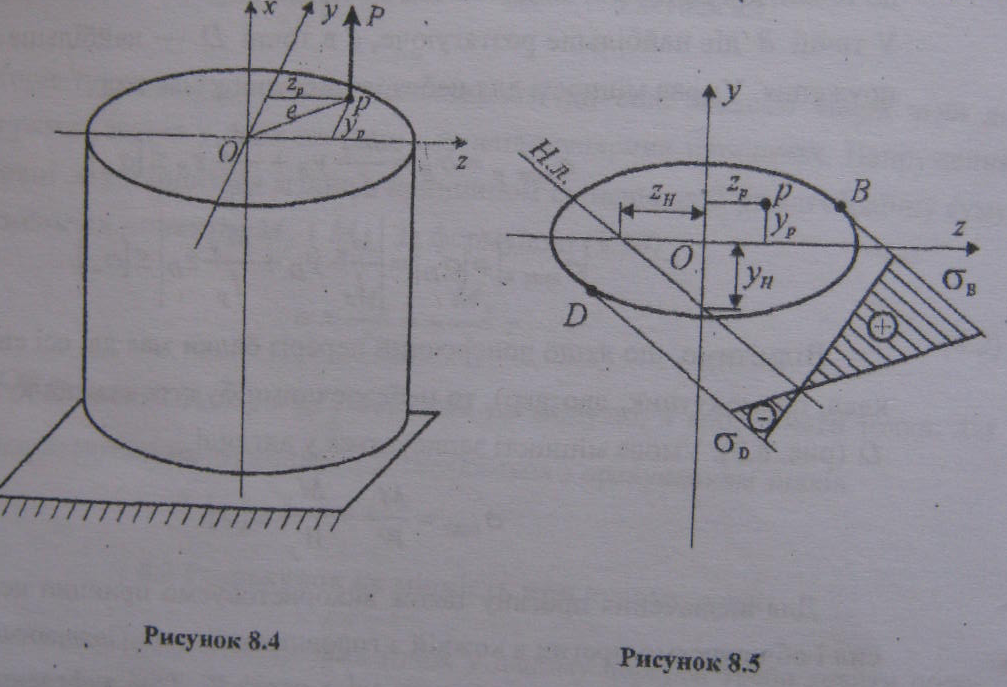
Позацентровий розтяг або стиск викликається навантаженням, рівнодійна якого Р проходить паралельно до осі стержня з ексцентриситетом е.

Нехай на стержень довільного перерізу діє одна сила Р, яка паралельна до осі стержня і перетинає будь-який поперечний переріз у точці р (рис. 8.4). Ко­ординати точки р в системі головних центральних осей позначимо z_р і y_p. В будь-якому поперечному перерізі внутрішній силові фактори дорівнюють:

N=P; M_y=Pz_y; M_z=Py_p. (8.10)

На основі принципу суперпозиції нормальне напруження а в довільній точці перерізу дорівнює сумі напружень від кожного силового фактору

(8.11)

Підставляючи (8.10) в (8.11), одержимо

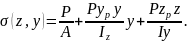(8.12)

Винесемо Р/А і врахуємо, що

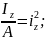
де і_z, i_y — головні радіуси інерції поперечного перерізу стержня. Tоді

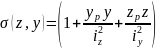. (8.13)

Формула (8.13) дає можливість знайти нормальні напруження в довільній точці поперечного перерізу стержня.

Тут z, у — координати довільної точки, а осі z, у вибирають так, щоб то­чка р лежала в 1-ій чверті.

Ми розглянули випадок, коли сила Р — розтягуюча. Якщо ж сила Р — стискаюча, то в формулі (8.13) перед Р треба записати знак мінус.