Тогда дифференциальное уравнение принимает вид
,
где
;
;
,
где
и
- алгебраические
величины угловой скорости и углового
ускорения переносного вращения; МК
— расстояние в данный момент от точки
М
до оси вращения.
Правая часть уравнения, кроме приложенных к точке сил, содержит переносную вращательную, переносную центробежную и кориолисову силы инерции.
2. Переносное
движение — равномерное вращение вокруг
неподвижной оси. В
этом случае
и
=0
и основное уравнение динамики
относительного движения точки примет
вид
.
3. Переносное
движение — поступательное неравномерное
криволинейное движение. В
этом
случае
и
,
а потому
уравнение
принимает
вид
,
где
;
.
4. Переносное
движение — поступательное прямолинейное
и равномерное движение. В
этом случае
и
,
а потому уравнение принимает вид
.
В правой части уравнения имеется только геометрическая сумма приложенных к точке сил, как в основном уравнении абсолютного движения точки, т. е. подвижная система отсчета Охуz является в этом случае тоже инерциальной системой.
Глава 2. Колебательное движение материальной точки
2.1. Виды колебательных движений материальной точки
Колебание или колебательное движение материальной точки - повторяющееся во времени движение точки около своего положения равновесия в двух противоположных направлениях. Необходимым условием такого положения является наличие восстанавливающей силы, которая возвращает точку в положение равновесия, если ее вывели из этого положения.
Такой силой может быть сила упругости связей, наложенных на материальную точку (рис. 3.14): пружины, рессоры, упругих оснований.
а) б)
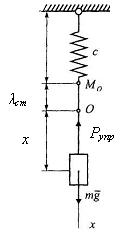
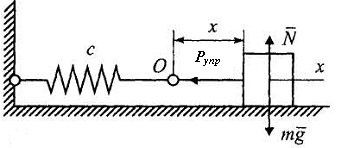
в)
Рис. 3.14
Величина силы упругости, как правило, принимается пропорциональной деформации (удлинению пружины или прогибу балки). Проекция этой силы на ось х направлена в сторону и равна
при выборе начала координат (рис. 3.14,б) в конце недеформированной пружины и
при выборе начала координат (рис. 3.14,а,в) в положении статического равновесия.
В формулах с
– коэффициент жесткости упругой связи,
-
статическая деформация под действием
силы тяжести, х
– отклонение точки от начала координат
(текущая координата).
В положении равновесия (рис. 3.14,а,в – точка О)
или
.
При колебании на
точку могут кроме восстанавливающей
силы действовать сила сопротивления
и возмущающая сила
.
Сила сопротивления – сила, препятствующая движению материальной точки. Это либо сила вязкого трения, либо сухого трения. В случае вязкого трения сила сопротивления при небольших скоростях движения точки в вязких жидкостях или газах пропорциональна первой степени скорости и направлена противоположно вектору скорости, т.е.
,
где
- коэффициент сопротивления.
Возмущающая сила – сила, зависящая от времени. Во многих технических задачах наибольший интерес представляют возмущающие силы, которые изменяются с течением времени по периодическому закону:
,
где Н
– максимальный
модуль или амплитуда возмущающей силы;
р
– частота изменения возмущающей силы,
равная числу полных циклов изменения
возмущающей силы за 2π с;
-
фаза изменения возмущающей силы; δ
– начальная фаза изменения возмущающей
силы.
В зависимости от совокупности этих сил, действующих на материальную точку, различают четыре основных случая колебательного движения точки:
1) свободные колебания, совершающиеся под действием только восстанавливающей силы;
2) свободные колебания, совершающиеся под действием восстанавливающей силы и силы сопротивления движению;
3) вынужденные колебания, совершающиеся под действием восстанавливающей силы и силы периодического характера, называемой возмущающей силой;
4) вынужденные колебания, совершающиеся под действием восстанавливающей силы, возмущающей силы и силы сопротивления движению.