Заключение

Данный курс содержит основы математического программирования в сжатом виде. Отдельные классы задач в лекциях не рассматривались. Дадим о них краткую информацию.

Задачи параметрического программирования содержат некоторые па-

раметры, от которых зависит целевая функция и ОДР. Если целевая функция представляет собой отношение (дробь) двух линейных функций, то имеет место

задача дробно-линейного программирования. Задача математического про- граммирования, содержащая случайные величины, называется задачей стохас- тического программирования. Если процесс решения задачи математическо-

го программирования является многоэтапным и оптимальные решения нахо- дятся для разных моментов времени, то речь идёт о задаче динамического программирования.

Студентам предлагается самостоятельно изучить эти типы задач (напри- мер, по учебному пособию [1]). При необходимости следует проконсультиро- ваться у преподавателя.

Приложения содержат лекционный материал для самостоятельного озна- комления. В этих лекциях рассматриваются некоторые практические задачи, сводящиеся к задачам математического программирования.

Автор будет признателен своим коллегам, студентам и всем интересую- щимся лицам за дельные рекомендации, которые могли бы способствовать улучшению качества лекций.

Приложение а. Инвестиционные задачи и нелинейное программирование

Лекция 13. ФОРМИРОВАНИЕ СТРУКТУРЫ ФОНДОВОГО ПОРТФЕЛЯ

План

1. Числовые характеристики ценных бумаг.

2. Методы выявления «перспективных» ценных бумаг.

1. Основной принцип работы на фондовом рынке соответствует житейской мудрости: «Никогда не клади все яйца в одну корзину». Инвестор не должен приобретать ценные бумаги только одного вида. Ему необходимы разнообра- зие, диверсификация вклада. Поэтому опытный инвестор формирует порт- фель ценных бумаг.

Пусть T – количество временных периодов, в течение которых велось наблюдение за ценными бумагами. На каждом из периодов рассчитывается эф-

_{фективность}

_{R(t ) . Число}

_{t = 1, 2,...,T}

_{характеризует номер периода. Эффектив-}

ность рассчитывается по формуле

^{R(t ) = S (t ) + d (t ) − S (t − 1) ⋅ 100% ,}

^{S (t − 1)}

_где

_{S (t) – цена акции в конце t -го периода,}

_{S (t − 1)}

_{– цена акции в конце (t − 1) -}

_{го периода,}

_{d (t )}

_{– дивиденды, начисленные в t -ом периоде.}

Реализацией случайной величины R является статистическая выборка, которую рассчитывают по ценам данной акции и начисляемым дивидендам. Эффективность конкретной i -й акции характеризуют оценкой математического

^{ожидания m}_i

– выборочной ожидаемой эффективностью, выборочной дис-

персией

^D_i ^{, выборочным средним квадратическим (стандартным) откло-}

^{нением σ i :}

_{m =} ¹

^{i T}

_T

_T

^∑

^{t =1}

R_i (t ) ,

_{D = 1 (R (t ) − m )2 ,}

T − 1

^{i ∑ i i}

^{t =1}

^σ _i ⁼

^D_i ^.

_число

Заметим, что в формуле для выборочной дисперсии в знаменателе стоит

_{T − 1. Эта поправка внесена с целью получения несмещённой оценки}

_{дисперсии. Поправкой обычно пренебрегают, если объем выборки T достаточ-}

_{но большой. Это означает, что при}

_{T < 20}

_{в формулу подставляют}

_{T − 1, а при}

_{T ≥ 20}

_{– подставляют T .}

Если дисперсия эффективности равна нулю, то эффективность не откло- няется от математического ожидания, т.е. нет неопределённости и риска. Чем больше дисперсия, тем в среднем больше отклонение, т.е. выше неопределён-

^{ность и риск. Поэтому величину дисперсии считают мерой риска, а σ i}

называ-

_{ют риском i -го актива. Инвестор заинтересован в увеличении ожидаемой эф-}

фективности

^m_i ^{. С другой стороны, важно уменьшить риск.}

Кроме индивидуальных числовых характеристик

^m_i ^,

^D_i ^,

^σ _i ^{, рассчиты-}

вают характеристики взаимовлияния активов – выборочные ковариации эффективностей:

₁ ^T

V = (R (t ) − m )(R

_{(t ) − m ) .}

T − 1

2

ij ^∑

t =1

i i j i

^{Заметим, что Vij}

^{= V ji}

^{и Vii = Di = σ i .}

^{2. Считается, что характеристик m}_i

^{и σ} _i

достаточно для отбора «перспектив-

^{ных» ценных бумаг в портфель. Акции с отрицательным показателем m}_i ^не

должны включаться в портфель. Оставшиеся ценные бумаги подлежат рас-

смотрению.

^{По сути дела, сравниваются пары чисел (mi ;σ i ) . Если какой-то актив за-}

^{ведомо «проигрывает» другому, то он исключается из портфеля. Такой способ}

отбора называют методом последовательных сравнений.

_{Например, если имеется возможность выбора между двумя акциями, при-}

чем

^m_i ^{> m} _j ^{, а}

^σ _i ^{= σ} _j ^{, то инвестор предпочтёт i -ю ценную бумагу. Если же}

^{mi = m j , а σ i > σ j , то инвестор выберет j -ю акцию. В ситуации}

^{инвестор предпочтет i -ю ценную бумагу.}

^{mi > m j , σ i < σ j}

Однако, если

^m_i ^{> m} _j ^,

^σ _i ^{> σ} _j

(или

^m_i ^{< m} _j ^,

^σ _i ^{< σ} _j ^{), то однозначного ре-}

шения нет и выбор инвестора будет зависеть от его склонности к риску. Реко- мендуется включать в портфель обе акции и уже внутри портфеля решать во- прос о том, какую часть капитала вкладывать в конкретную ценную бумагу.

Пример 1. В табл. 1 приведены цены акций

^S_i ^{(t ) (грн.) пяти корпораций}

^{за 10 биржевых дней. Здесь i – номер акции ( i = 1, 5 ), t – номер биржевого дня}

^{( t = 1,10 ).}

^{Табл. 1. Цены акций пяти корпораций}

t	1	2	3	4	5	6	7	8	9	10
S1 (t )	1	1	3	3	5	10	15	15	16	18
S2 (t )	1	1	3	3	10	5	15	15	16	16
S3 (t )	2	3	4	4	5	10	15	15	17	17
S4 (t )	2	2	4	4	10	5	15	15	18	19
S5 (t )	18	16	15	15	10	1	1	3	3	5

Требуется: 1) провести статистический анализ эффективностей акций; 2)

отобрать «перспективные» ценные бумаги в фондовый портфель.

^{Решение. 1) Наличие 10-ти данных по стоимостям акций определяет T = 9}

^{временных периодов, на каждом из которых рассчитывается эффективность}

^R_i ^{(t ) ,}

^{i = 1, 5 ,}

^{t = 1, 9 . От выборок с 10-ю ценами акций (грн.) осуществляется}

переход к выборкам с 9-ю эффективностями (%) (табл. 2):

_{Табл. 2. Эффективности акций пяти корпораций}

t	1	2	3	4	5	6	7	8	9
R1 (t )	0	200	0	66,67	100	50	0	6,67	12,5
R2 (t )	0	200	0	233,33	-50	200	0	6,67	0
R3 (t )	50	33,33	0	25	100	50	0	13,33	0
R4 (t )	0	100	0	150	-50	200	0	20	5,56
R5 (t )	-11,11	-6,25	0	-33,33	-90	0	200	0	66,67

1

Например,

_{R (9) =} ^S₁ ^{(10) − S}₁ ⁽⁹⁾ _{⋅ 100% =} ^{18 − 16} _{⋅ 100% = 12, 5% .}

^S₁ ^{(9) 16}

^{По всем выборкам рассчитаем выборочные средние m}_i

и средние квадра-

^{тические отклонения σ} _i

эффективностей. В Microsoft Excel – с помощью функ-

ций СРЗНАЧ( ) и СТАНДОТКЛОН( ), соответственно. Функции вызываются опцией «f_x» – «Вставка функции». Формируем табл. 3.

_{Таблица 3. Индивидуальные числовые характеристики акций}

i	mi (%)	σ i (%)
1	48,4259	67,1188
2	65,5556	110,8553
3	30,1852	33,0030
4	47,2840	83,1482
5	13,9969	80,6651

2) Определим «перспективные» ценные бумаги (рис. 1).

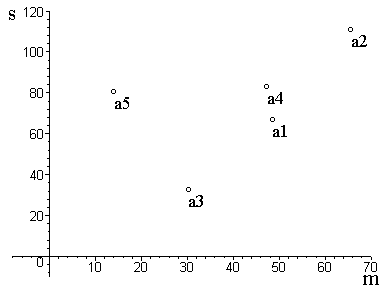
Рис. 1. Точечная диаграмма отбора акций в портфель

Методом последовательных сравнений убеждаемся в том, что «перспек- тивными» акциями являются а3, а1, а2. Из них и следует формировать портфель ценных бумаг.

Можно использовать и другой способ отбора. На точечной диаграмме строится нижняя огибающая ломаная, все звенья которой имеют положитель- ный коэффициент наклона (рис. 2).

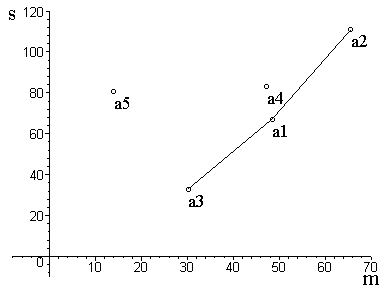
Рис. 2. Графический способ отбора акций в портфель

Точки, попавшие на эту ломаную, определяют «перспективные» акции. Судя по рис. 2, в портфеле ценных бумаг должны остаться акции а3, а1, а2. Та- кой способ отбора называют методом нижней огибающей ломаной.