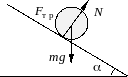
Скатывание цилиндра с наклонной плоскости

Пусть цилиндр радиуса скатывается без скольжения по наклонной плоскости. Ось x удобно выбрать вдоль наклонной плоскости. На цилиндр действуют сила тяжести , сила трения и сила реакции опоры . Уравнения движения для цилиндра имеют вид

,

.

Учитывая, что , а , получим

или

, .

Таким образом, цилиндр скатывается с постоянным ускорением, величина которого зависит от угла наклона .

2.9. Движение твердого тела, закрепленого в точке

В общем случае движения вектор угловой скорости изменяет свое направление в пространстве и свою ориентировку относительно тела, то есть мгновенная ось вращения меняет свою ориентировку. Удобно рассматривать это движение в системе координат, жестко связанной с телом. Начало координат естественно поместить в точку закрепления тела. Она находится в покое. Получающиеся при этом уравнения движения называются уравнениями Эйлера.

Уравнение движения центра масс тела имеет вид

, (2.16)

где – радиус-вектор центра масс тела, проведенный из точки его закрепления

Оси связанной с телом системы координат удобно направить по главным осям инерции. В этом случае тензор инерции сводится к трем своим главным значениям а момент импульса приобретает простой вид: , , , причем , , – проекции угловой скорости на движущиеся вместе с телом оси координат. В уравнении моментов производная вычисляется относительно инерциальной системы координат. Необходимо определить эту величину относительно движущейся системы координат, жестко связанной с телом.

Пусть некоторый вектор задан компонентами относительно системы координат :

,

где – единичные орты связанной с телом системы координат. С течением времени изменяются проекции на движущиеся оси координат и ориентировка осей координат относительно инерциальной системы отсчета. Имеем

. (2.17)

Скорость точки вращающегося тела, радиус-вектор которой , равна . Аналогично, следя за концом вектора , проведенным из точки на оси вращения, находим . Такой же вид имеют производные от и . Следовательно,

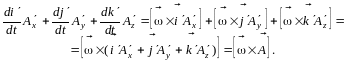
Поэтому формула (2.17) может быть записана в виде

,

где – производная от , вычисленная в предположении, что оси неподвижны. Эта формула справедлива для любых векторов . Применяя ее к вектору в уравнении моментов, можно представить уравнение моментов следующим образом:

. (2.18)

Принимая во внимание, что , , , уравнение (2.18) перепишем в проекциях на оси движущейся системы координат:

,

, (2.19)

.

Подчеркнем еще раз, что все величины в этих уравнениях отнесены к движущимся осям координат, жестко связанных с телом, штрихи же не проставлены лишь для упрощения написания формул.

Эти уравнения называют уравнениями Эйлера. Они в принципе всегда позволяют определить движение тела, закрепленного в одной точке, хотя практически решение может быть весьма сложным и трудно выполнимым.

2.10. Свободные оси

Допустим, что твердое тело вращается вокруг закрепленной оси, например оси, проходящей через неподвижные подшипники. Со стороны подшипников на тело действуют силы реакции. Их момент относительно оси равен нулю. Предположим, что других сил нет, поэтому моменты сил равны нулю.

Примем за начало системы координат центр масс, а оси системы координат, жестко связанной с телом, направим по центральным главным осям. Моменты инерции в этом случае являются центральными главными моментами инерции тела. Уберем подшипники и выясним, при каких условиях движение тела не изменится, то есть останется вращением вокруг выбранной оси. Ось вращения, сохраняющая направление в пространстве неизменным без воздействия извне, называется свободной осью.

Из (2.19) непосредственно следует, что невозможно такое свободное вращение тела, при котором угловая скорость сохраняет свое абсолютное значение и ориентировку относительно тела, но не совпадает по направлению ни с одной из центральных главных осей с разными моментами инерции. Допустим, что это возможно, то есть, что , , . Тогда из уравнений следует, что должно быть

, , . (2.20)

Эти соотношения можно одновременно удовлетворить только в том случае, если две проекции угловой скорости одновременно равны нулю. А это означает, что угловая скорость совпадает по направлению с одной из центральных главных осей. Пусть, например, . Тогда соотношения (2.20) будут удовлетворены. Угловая скорость при этом направлена вдоль оси X, то есть вдоль центральной главной оси.

Таким образом, свободное вращение твердого тела возможно лишь вокруг центральных главных осей. Эти оси и называются свободными. Моменты инерции относительно этих осей, вообще говоря, различны. Можно доказать, что вращение тела будет устойчивым только относительно центральной главной оси с максимальным или минимальным моментом инерции. Вращение вокруг центральной главной оси со средним моментом инерции неустойчиво. При небольшом случайном отклонении оси вращения от этого направления возникают силы, увеличивающие отклонение. Это обстоятельство можно наглядно продемонстрировать на таком опыте. У тела в виде прямоугольного параллелепипеда центральными главными осями являются три взаимно перпендикулярные оси, проходящие через его геометрический центр параллельно сторонам. Параллелепипед имеет наибольшие и наименьшие моменты инерции относительно осей, параллельных его самой длинной и самой короткой сторонам. Если его подбросить с одновременным вращением вокруг одной из этих осей, то движение происходит устойчиво с сохранением направления оси вращения. Если же его вращать вокруг оси, параллельной средней стороне, то устойчивого движения не получается и тело начинает беспорядочно кувыркаться.