2.3. Уравнения движения

Твердое тело может рассматриваться как система материальных точек. Поэтому все утверждения и уравнения о системе материальных точек применимы для твердого тела. Эти уравнения имеют вид

, (2.2)

. (2.3)

Этих двух векторных уравнений достаточно для того, чтобы полностью определить движение твердого тела при заданных внешних силовых полях и начальных условиях. В частном случае при вращении твердого тела вокруг неподвижной оси уравнение (2.3) принимает вид

.

Для тел, имеющих симметричную форму, вычисление момента инерции не вызывает затруднений.

2.4. Вычисление момента инерции относительно оси вращения

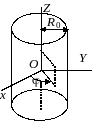
Для вычисления момента инерции твердого тела относительно оси вращения используется формула (1.9). Однако удобнее применить интегрирование, переходя к непрерывному распределению масс. Пусть плотность тела . Тогда в элементе объема заключена масса . Если вычислять момент инерции тела относительно оси z, то формула (1.9) принимает вид

(2.4)

и интегрирование распространяется на весь объем тела.

В качестве примера определим момент инерции однородного цилиндра радиусом и высотой h относительно оси, совпадающей с его осью. Направим ось Z системы координат вдоль оси цилиндра, а начало системы координат (точка О) поместим на оси в середине высоты. Плотность цилиндра постоянна, то есть . Интеграл (2.4) записывается

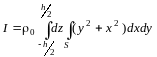, (2.5)

где S – площадь сечения цилиндра. Вычисление удобно вести в цилиндрической системе координат, направив ось Z вдоль оси симметрии цилиндра. Тогда

, , ,

.

Поэтому вместо (2.5) получаем

.

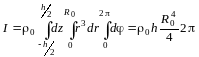Принимая во внимание, что объем цилиндра равен и, следовательно, величина является его массой, окончательно находим

. (2.6)

Аналогично вычисляются и другие моменты. Например, момент инерции однородного шара относительно оси, проходящей через его центр, равен , где m – масса шара, – его радиус. Момент инерции тонкого диска относительно оси, проходящей через центр диска перпендикулярно его плоскости, дается формулой (2.6), а его момент относительно оси, проходящей через центр диска и лежащей в плоскости диска, равен .

2.5. Теорема Гюйгенса

Вычисление моментов инерции относительно оси во многих случаях облегчает теорема Гюйгенса, связывающая моменты инерции относительно двух параллельных осей, одна из которых проходит через центр масс тела. Пусть ось проходит через центр масс. Радиус-вектор точки с массой , отсчитываемый от этой оси, в плоскости, перпендикулярной оси, обозначим , а от оси AB, параллельной оси , но не проходящей через центр масс, . Проведем от оси к оси AB в этой плоскости вектор . Пусть – момент инерции относительно оси, проходящей через центр масс, а I – относительно оси AB, не проходящей через центр масс. По определению моментов инерции имеем

, .

На рисунке непосредственно видно, что и, следовательно, . Поэтому получаем

.

Учтем, что по определению оси, проходящей через центр масс, а – масса тела. Тогда для момента инерции относительно оси AB получаем следующее выражение:

. (2.7)

Эта формула выражает теорему Гюйгенса. Она позволяет по моменту инерции относительно некоторой оси, проходящей через центр масс, легко вычислить момент инерции относительно любой другой параллельной оси.

Рассмотрим, например, цилиндр, момент инерции которого относительно его оси дается формулой (2.6). Центр масс цилиндра расположен на его оси и поэтому (2.6) является моментом инерции относительно оси, проходящей через центр масс. Момент инерции цилиндра относительно оси AB, лежащей на поверхности цилиндра параллельно его оси, находим по формуле (2.7):

.

Если бы этот момент определять по формуле (2.4), то вычисления оказались бы значительно сложнее.

Момент инерции шара относительно оси AB, касающейся его поверхности, также легко находится с помощью формулы (2.7):

,

где учтено, что момент инерции шара относительно оси, проходящей через центр масс, равен .