
- •Заступник директора з розглянуто
- •Пояснювальна записка
- •Тематичний план
- •Визначник
- •Властивості визначників
- •Система лінійних рівнянь
- •Питання для самоконтролю.
- •Векторна алгебра Додавання векторів. Множення вектора на скаляр
- •Прямокутні координати вектора в просторі
- •Скалярний добуток двох векторів
- •Векторний добуток векторів
- •Рівняння прямої у просторі
- •Пряма на площині
- •Питання для самоконтролю.
- •Криві іі-го порядку
- •Гіпербола.
- •Парабола.
- •Питання для самоконтролю.
- •Вступ до аналізу Комплексні числа
- •Питання для самоконтролю
- •Змінні величини і функції
- •Границі послідовності та функції. Нескінченно малі та нескінченно великі
- •Границя відношення при
- •Порівняння нескінченно малих функцій
- •Неперервність функції
- •Асимптоти
- •Геометричний і механічний зміст похідної. Рівняння дотичної та нормалі до графіків функції
- •Диференціал функції
- •Похідні і диференціали вищих порядків
- •Застосування похідних до дослідження функцій Теореми про середнє значення
- •Правило Лопіталя
- •Зростання і спадання функції. Екстремум.
- •Необхідна умова існування екстремуму.
- •Достатні умови існування екстремуму.
- •Питання для самоконтролю
- •Інтегрування підстановкою та безпосередньо
- •Інтегрування по частинах
- •Інтеграли виду Вправи
- •Інтегрування раціональних алгебраїчних функцій
- •Інтегрування дуяких ірраціональних алгебраїчних функцій
- •Інтегрування тригонометрчних функцій
- •Питання для самоконтролю
- •Визначений інтеграл
- •Обчислення площ
- •Об’єм тіла обертання
- •Обчислення довжини дуги кривої
- •Питання для самоконтролю
- •Диференційні рівняння першого порядку
- •Однорідні диференційні рівняння першого порядку
- •Лінійні диференційні рівняння першого порядку
- •Лінійні диференційні рівняння другого порядку
- •Питання для самоконтролю
- •Формула і ряд Тейлора та їх застосування
- •Питання для самоконтролю
- •Рекомендована література
Застосування похідних до дослідження функцій Теореми про середнє значення
Дослідження функцій за допомогою похідних ґрунтується на деяких основних теоремах диференціального числення.
Теорема Лагранжа.
Нехай функція
задовольняє
умовам: 1)
неперервна на
![]() 2)
диференційована на (
).
Тоді існує точка
2)
диференційована на (
).
Тоді існує точка
![]() така, що
така, що
![]() .
Ця формула називається формулою Лагранжа,
або формулою скінчених приростів.
.
Ця формула називається формулою Лагранжа,
або формулою скінчених приростів.
Теорема Коші.
Нехай функція
і
![]() задовольняють умовам: 1)
і
неперервні на
2)
і
диференційовані на (
);
3)
задовольняють умовам: 1)
і
неперервні на
2)
і
диференційовані на (
);
3)
![]() в усіх точках
в усіх точках
![]() .
Тоді існує точка
така, що
.
Тоді існує точка
така, що
![]() .
Ця формула називається формулою Коші.
.
Ця формула називається формулою Коші.
Вправи
Для функції
 записати формулу Лагранжа на відрізку
записати формулу Лагранжа на відрізку
 і визначити значення
і визначити значення
 :
:
1)
,
[0;1]; 2)
![]() ,
[1;2].
,
[1;2].
записати формулу Коші для функцій:
1)
![]() і
=
і
=![]() на відрізку [1;2];
на відрізку [1;2];
2)
![]() і
=
і
=![]() на відрізку [
на відрізку [![]() ].
].
Визначити значення
![]() .
.
Довести, що рівняння
 має лише один дійсний корінь.
має лише один дійсний корінь.Довести, що рівняння
 ,
яке має корінь
(перевірте), не має інших дійсних коренів.
,
яке має корінь
(перевірте), не має інших дійсних коренів.
Правило Лопіталя
Найбільш простим і ефективним методом розкриття невизначеностей є правило Лопіталя.
Нехай функції і :
1) диференційовані в деякому околі точки а за винятком, можливо, самої точки а, причому у цьому околі; 2) одночасно є нескінченно малими або нескінченно великими в точці а;
3) існує
![]() (можливо, нескінченна). Тоді існує
(можливо, нескінченна). Тоді існує
![]() ,
причому
,
причому
![]() .
.
Правила Лопіталя діють також
при
![]() ,
,
![]() ,
,
![]() і у випадках однобічних границь. Вони
дозволяють розкривати невизначеності
типу
і
.
і у випадках однобічних границь. Вони
дозволяють розкривати невизначеності
типу
і
.
Правило Лопіталя можна застосовувати кілька разів.
Вправи
Застосовуючи правило Лопіталя, обчислити границі:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]()
Невизначеності типів
![]() і
шляхом простих алгебраїчних перетворень
зводяться спочатку до типів
і
,
до яких і застосовується правило
Лопіталя.
і
шляхом простих алгебраїчних перетворень
зводяться спочатку до типів
і
,
до яких і застосовується правило
Лопіталя.
11)
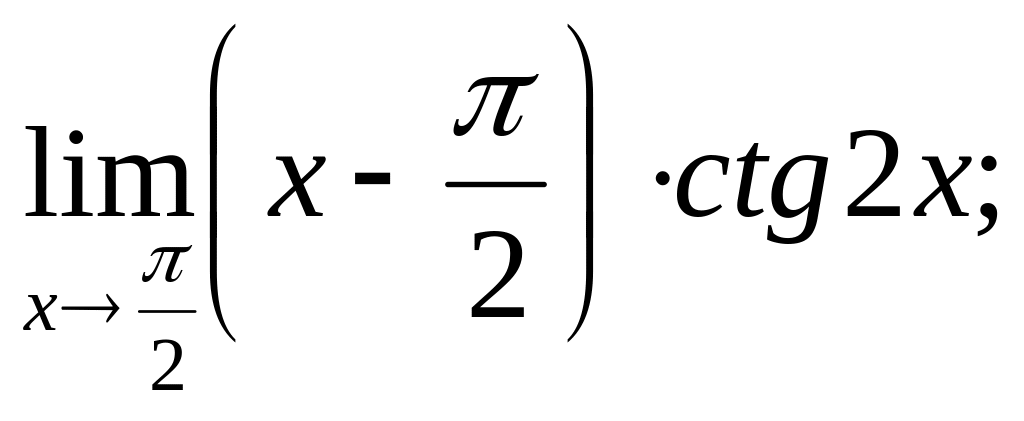 12)
12)
![]()
13)
![]() 14)
14)
![]()
15)
![]() 16)
16)
![]()
17)
![]() 18)
18)
![]()
Невизначеність типів
![]() ,
які зустрічаються при обчисленні границь
функцій вигляду
,
які зустрічаються при обчисленні границь
функцій вигляду
![]() зводяться до невизначеності типу
.
зводяться до невизначеності типу
.
19)
![]() 20)
20)
![]() 21)
21)
![]() 22)
22)
![]() 23)
23)
![]() 24)
24)
![]() 25)
25)
![]()
Зростання і спадання функції. Екстремум.
Якщо
![]() для всіх
для всіх
![]() ,
то функція зростає (спадає) на
.
,
то функція зростає (спадає) на
.
Функція
в точці
має максимум (мінімум), якщо існує такий
окіл 0![]() точки
,
що для всіх
точки
,
що для всіх
![]() з цього околу
з цього околу
![]()
Максимум (мінімум) функції в точці називається екстремум функції в цій точці, а сама точка - точкою екстремуму.
Точки
![]() ,
в яких
,
в яких
![]() ,
називаються стаціонарними,а разом з
точками, де функція недиференційована
(але неперервна) – критичними точками
функції.
,
називаються стаціонарними,а разом з
точками, де функція недиференційована
(але неперервна) – критичними точками
функції.
Необхідна умова існування екстремуму.
Якщо функція має екстремум у точці , то ця точка є критичною.
Достатні умови існування екстремуму.
Нехай функція диференційована в деякому околі точки , окрім, можливо, самої точки , в якій функція неперервна.
Якщо при переході аргументу через точку похідна змінює знак з плюса на мінус, то функція в цій точці має максимум; якщо знак змінюється з мінуса на плюс, то функція має мінімум.
Нехай функція
двічі диференційована і
.
Тоді в точці
функція
має максимум, якщо
![]() і мінімум, якщо
і мінімум, якщо
![]() .
.
Вправи
Знайти проміжки зростання і спадання функцій:
1)
![]() 2)
2)
![]() 3)
3)
![]() 4)
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]() 10)
10)
![]() 11)
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
Визначити екстремуми функцій:
1)
![]() 2)
2)
![]() 3)
3)
![]() ;
4)
;
4)
![]() 5)
5)
![]() 6)
6)
7)
![]() 8)
9)
8)
9)
![]() ;
10)
;
10)
![]() 11)
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]() 15)
15)
![]()
16)
![]() 17)
17)
![]() 18)
18)
![]()
19)
![]() 20)
20)
![]()
Розв’язати задачі:
З бляшаного круга радіуса R вирізають сектор з центральним кутом із нього скручують конічну лійку. При якому значені кута об’єм лійки буде найбільшим?
Якою повинна бути висота конуса, вписаного в кулю радіуса R, щоб його бокова поверхня була найбільшою?
Серед прямокутників з даним периметром
 найти
такий, площа якого найбільша.
найти
такий, площа якого найбільша.На сторінці книги друкований текст повинен займати 432 см . Поля зверху і знизу повинні бути по 2 см, а справа і зліва по 1,5 см. Обчислити най економніші розміри паперу.(21 см; 28 см).
Знайти висоту прямого кругового конусу найменшого об’єму, який описаний навколо кулі радіусом R. (8 R).
