
- •Основные понятия теория множеств
- •Операции над множествами
- •Функция, ее область определения, способы задания Понятие функции одной переменной
- •Способы задания функций:
- •Сложные и обратные функции
- •Предел функции Предел функции в бесконечности и в точке
- •Признаки существования предела
- •Бесконечно малые функции, их свойства Бесконечно малые величины
- •Связь бесконечно малых величин с пределами функций
- •Свойства бесконечно малых величин
- •Бесконечно большие функции Бесконечно большие величины
- •Свойства бесконечно больших величин
- •Связь между бесконечно малыми и бесконечно большими величинами
- •Сравнение бесконечно малых функций, их эквивалентность Основные эквивалентности.
- •Основные теоремы о пределах Основные теоремы о пределах. Признаки существования предела
- •Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.Е.
- •Предел произведения конечного числа функций равен произведению пределов этих функций, т.Е.
- •Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.Е.
- •Замечательные пределы Первый замечательные предел.
- •Второй замечательный предел.
- •Раскрытие неопределенности
- •Непрерывность функции
- •Точки разрыва, их классификация Точки разрыва функции
- •Асимптоты
- •Производная, ее геометрический, физический, экономический смысл экономический смысл производной
- •Физический смысл производной.
- •Определение производной
- •Задача о касательной
- •Правила дифференцирования
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •Производные основных элементарных функций Производные основных элементарных функций (таблица производных)
- •Дифференцирование сложных функций Производная сложной функции
- •Дифференцирование функций, заданных неявно и параметрически
- •Дифференциал функции, его свойства Понятие дифференциала и его геометрический смысл
- •Свойства дифференциала аналогичны свойствам производной.
- •Инвариантность формы дифференциала
- •Приближенные вычисления с помощью дифференциала
- •Производные и дифференциалы высших порядков
- •Теорема ферма
- •Теоремы роля, коши, Лагранжа
- •Правило лопиталя
- •Признаки монотонности функции Признаки возрастания и убывания функции.
- •Экстремумы(локальные)функции
- •Наибольшее и наименьшее значение функции
- •Признаки вогнутости и выпуклости графиков, точки перегиба
- •Неопределенный интерграл, свойства Понятие первообразной и неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основная таблица интегралов Некоторые табличные интегралы
- •Метод непосредственного интегрирования
- •Интегрирование по частям
- •Замена переменной в неопределенном интеграле
- •Интегральная сумма определенный интеграл, его геометрический смысл
- •Геометрический смысл определенного интеграла.
- •Экономический смысл определенного интеграла.
- •Свойства определенного интеграла Свойства определенного интеграла
- •Формула ньютона-лейбница Определенный интеграл с переменным верхним пределом
- •Формула Ньютона-Лейбница.
- •Интегрирование по частям и замена переменной в опр. Интеграле Методы вычисления определенного интеграла
- •Несобственные интегралы Несобственные интегралы с бесконечными пределами интегрирования
- •Дифференциальное уравнение первого порядка, их общее частное особое решение
- •Задача коши, теорема сущ. Единственности решения задачи коши Задача о построении математической модели демографического процесса. Задача Коши
- •Уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка Линейные дифференциальные уравнения 1-го порядка.
- •Дифф. Уравнения высших порядков, их общее и частной решение,задача коши
- •.Линейные диффер. Уравнения н-ого порядка,структура решения
- •Линейные однородные дифф уравнения с постоянными коэф. Метод Эйлера Однородные дифференциальные уравнения 1-го порядка.
- •Линейные неоднородные диф уравнения с правой частью специального вида. Метод неопр. Коэф
- •Определение функции нескольких переменных, геометрическая интерпретация в возможных случаях предел и непрерывность
- •Частное и полное приращение функции
- •Частные производные Основные понятия. Частные производные
- •Частные производные функции двух переменных
- •Полный дифференциал
- •Производная по направлению
- •Градиент
- •Локальный экстремум
- •Условный экстремум
Правило лопиталя
Будем говорить, что отношение f(x)/g(x) представляет собой неопределенность вида 0/0 при xа, если limxаf(x)= limxаg(x)=0. Раскрыть эту неопредел-сть – это значит найти limxаf(x)/g(x), если он существует.
Теорема №1: Пусть f(x) и g(x) определены и дифференцируемы в окрестности точки х=а, за исключением, быть может, самой точки a, limxаf(x)= limxаg(x)=0, g(x) и g'(x)0 в этой окрестности. Тогда, если существует limxаf'(x)/g'(x), то существует limxаf(x)/g(x) и имеет место равенство limxаf(x)/g(x)=limxаf'(x)/g'(x) {1}. Доказательство: Будем считать, что а – конечное число. (В случае а= см. ниже замечание 3.) Доопределим функции f и g в точке х=а, полагая f(a)=g(a)=0. Тогда эти функции будут непрерывны в точке а. Рассмотрим отрезок [а,х], где х>а или х<а. На [а,х] функции f и g непрерывны, а на (а,x) дифференцируемы, поэтому по теореме Коши существует точка S такая, что (f(x)–f(a))/(g(x)–g(a))=f'()/g'() (при (а,x)) или f(x)/g(x)=f'()/g'().
Когда хa и, то и a, поэтому в силу условия теоремы имеем limxаf(x)/g(x)=limаf'()/g'() =limxаf'(x)/g'(x) {2}при условии, что предел в правой части равенства существует. Этим теорема доказана. Замечания: [1] Если предел справа в {1}не существует, то предел слева может существовать.
[2] Если выражение f'(x)/g'(x) представляет неопределенность вида 0/0 г и функции f'(x), g'(х) удовлетворяют условию теоремы №1, то limxаf(x)/g(x)=limxаf'(x)/g'(x)= limxаf''(x)/g''(x)
П![]() ри
этом эти равенства надо понимать в том
смысле, что если существует третий
предел, то существует и второй и
первый. Теорема
№2 (/):
Пусть f
и g
определены и дифференцируемы в окрестности
точки х=a,
limxaf(х)=
limxag(х)=,
g(x)
и g'(x)0
в этой окрестности, тогда, если
limxаf'(x)/g'(x),
то
limxаf(x)/g(x).
[3]
Если а=,
то замена х=1/t
сводит дело к а=0:
ри
этом эти равенства надо понимать в том
смысле, что если существует третий
предел, то существует и второй и
первый. Теорема
№2 (/):
Пусть f
и g
определены и дифференцируемы в окрестности
точки х=a,
limxaf(х)=
limxag(х)=,
g(x)
и g'(x)0
в этой окрестности, тогда, если
limxаf'(x)/g'(x),
то
limxаf(x)/g(x).
[3]
Если а=,
то замена х=1/t
сводит дело к а=0:
Выражаемые теоремами №1, 2 правила, в силу которых вычисление предела отношения функций может быть сведено к вычислению предела отношения их производных, наз. правилом Лопиталя по имени математика, который сформулировал это правило, правда, для весьма простых случаев. Впрочем, это правило было известно И. Бернулли до Лопиталя.
Признаки монотонности функции Признаки возрастания и убывания функции.
Определение.
Функция
 называется возрастающей
на интервале
,
если для любых точек
называется возрастающей
на интервале
,
если для любых точек
 из этого интервала при выполнении
условия
из этого интервала при выполнении
условия
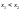 выполняется неравенство
выполняется неравенство
 (большему значению аргумента соответствует
большее значение функции).
(большему значению аргумента соответствует
большее значение функции).
Определение.
Аналогично, функция
 называется убывающей
на интервале
называется убывающей
на интервале
 ,
если для любых точек
,
если для любых точек
 из этого интервала при выполнении
условия
из этого интервала при выполнении
условия
 выполняется неравенство
выполняется неравенство
 (большему значению аргумента соответствует
меньшее значение функции).
(большему значению аргумента соответствует
меньшее значение функции).
Возрастающие
на интервале
 и убывающие на интервале
и убывающие на интервале
 функции называются монотонными
на интервале
функции называются монотонными
на интервале
 .
.
Знание производной дифференцируемой функции позволяет находить интервалы ее монотонности.
Теорема
(достаточное условие возрастания
функции).
Если производная дифференцируемой на
интервале
 функции
функции
 положительна на интервале
положительна на интервале
 ,
то функция
монотонно возрастает на этом интервале.
,
то функция
монотонно возрастает на этом интервале.
Доказательство.
Зафиксируем любые точки
на интервале
 такие, что
такие, что
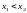 .
.
Тогда
по следствию из теоремы Лагранжа
 ,
где
,
где
 .
По условию на всем интервале
.
По условию на всем интервале
 ,
то есть
,
то есть
 ,
следовательно,
,
следовательно,
 .
Таким образом,
действительно возрастает на
,
что и требовалось доказать.
.
Таким образом,
действительно возрастает на
,
что и требовалось доказать.
Теорема
(достаточное условие убывания функции).
Если производная дифференцируемой на
интервале
функции
 отрицательна на интервале
отрицательна на интервале
 ,
то функция
монотонно убывает на этом интервале.
,
то функция
монотонно убывает на этом интервале.
Г

 тупые углы, а на интервалах возрастания
– острые (см. рис. 4).
тупые углы, а на интервалах возрастания
– острые (см. рис. 4).
Алгоритм
нахождения интервалов монотонности
функции
 .
.
Найти
 .
.Найти нули производной.
На числовой оси отметить область определения , нули производной и те точки, где производная не существует.
На каждом из полученных интервалов определить знак производной
 .
.Сделать вывод о возрастании или убывании функции
 на каждом интервале.
на каждом интервале.
Пример. Пусть .
Найдем
.
Найдем
 .
Далее,
.
Далее,
 при
при
 и при
и при
 .
Имеем, что
.
Имеем, что
 при
при
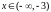 и при
и при
 ,
и
,
и
 при
при
 .
Это значит, что при
.
Это значит, что при
 и при
и при
 функция
функция
 возрастает, а при
возрастает, а при
 функция убывает.
функция убывает.
