- •Основные понятия теория множеств
- •Операции над множествами
- •Функция, ее область определения, способы задания Понятие функции одной переменной
- •Способы задания функций:
- •Сложные и обратные функции
- •Предел функции Предел функции в бесконечности и в точке
- •Признаки существования предела
- •Бесконечно малые функции, их свойства Бесконечно малые величины
- •Связь бесконечно малых величин с пределами функций
- •Свойства бесконечно малых величин
- •Бесконечно большие функции Бесконечно большие величины
- •Свойства бесконечно больших величин
- •Связь между бесконечно малыми и бесконечно большими величинами
- •Сравнение бесконечно малых функций, их эквивалентность Основные эквивалентности.
- •Основные теоремы о пределах Основные теоремы о пределах. Признаки существования предела
- •Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.Е.
- •Предел произведения конечного числа функций равен произведению пределов этих функций, т.Е.
- •Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.Е.
- •Замечательные пределы Первый замечательные предел.
- •Второй замечательный предел.
- •Раскрытие неопределенности
- •Непрерывность функции
- •Точки разрыва, их классификация Точки разрыва функции
- •Асимптоты
- •Производная, ее геометрический, физический, экономический смысл экономический смысл производной
- •Физический смысл производной.
- •Определение производной
- •Задача о касательной
- •Правила дифференцирования
- •Основные правила дифференцирования
- •Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.Е.
- •5. Производная частного двух дифференцируемых функций может быть найдена по формуле
- •Производные основных элементарных функций Производные основных элементарных функций (таблица производных)
- •Дифференцирование сложных функций Производная сложной функции
- •Дифференцирование функций, заданных неявно и параметрически
- •Дифференциал функции, его свойства Понятие дифференциала и его геометрический смысл
- •Свойства дифференциала аналогичны свойствам производной.
- •Инвариантность формы дифференциала
- •Приближенные вычисления с помощью дифференциала
- •Производные и дифференциалы высших порядков
- •Теорема ферма
- •Теоремы роля, коши, Лагранжа
- •Правило лопиталя
- •Признаки монотонности функции Признаки возрастания и убывания функции.
- •Экстремумы(локальные)функции
- •Наибольшее и наименьшее значение функции
- •Признаки вогнутости и выпуклости графиков, точки перегиба
- •Неопределенный интерграл, свойства Понятие первообразной и неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основная таблица интегралов Некоторые табличные интегралы
- •Метод непосредственного интегрирования
- •Интегрирование по частям
- •Замена переменной в неопределенном интеграле
- •Интегральная сумма определенный интеграл, его геометрический смысл
- •Геометрический смысл определенного интеграла.
- •Экономический смысл определенного интеграла.
- •Свойства определенного интеграла Свойства определенного интеграла
- •Формула ньютона-лейбница Определенный интеграл с переменным верхним пределом
- •Формула Ньютона-Лейбница.
- •Интегрирование по частям и замена переменной в опр. Интеграле Методы вычисления определенного интеграла
- •Несобственные интегралы Несобственные интегралы с бесконечными пределами интегрирования
- •Дифференциальное уравнение первого порядка, их общее частное особое решение
- •Задача коши, теорема сущ. Единственности решения задачи коши Задача о построении математической модели демографического процесса. Задача Коши
- •Уравнения с разделяющимися переменными
- •Линейные уравнения первого порядка Линейные дифференциальные уравнения 1-го порядка.
- •Дифф. Уравнения высших порядков, их общее и частной решение,задача коши
- •.Линейные диффер. Уравнения н-ого порядка,структура решения
- •Линейные однородные дифф уравнения с постоянными коэф. Метод Эйлера Однородные дифференциальные уравнения 1-го порядка.
- •Линейные неоднородные диф уравнения с правой частью специального вида. Метод неопр. Коэф
- •Определение функции нескольких переменных, геометрическая интерпретация в возможных случаях предел и непрерывность
- •Частное и полное приращение функции
- •Частные производные Основные понятия. Частные производные
- •Частные производные функции двух переменных
- •Полный дифференциал
- •Производная по направлению
- •Градиент
- •Локальный экстремум
- •Условный экстремум
основные понятия теория множеств
операции над множествами
функция, ее область определения, способы задания
сложные и обратные функции
предел функции
бесконечно малые функции, их свойства
бесконечно большие функции
сравнение бесконечно малых функций, их эквивалентность
основные теоремы о пределах
замечательные пределы
раскрытие неопределенности
непрерывность функции
точки разрыва, их классификация
асимптоты
производная, ее геометрический, физический, экономический смысл
правила дифференцирования
производные основных элементарных функций
дифференцирование сложных функций
дифференцирование функций, заданных неявно и параметрически
дифференциал функции, его свойства
производные и дифференциалы высших порядков
теорема ферма
теоремы роля, коши, Лагранжа
правило лопиталя
признаки монотонности функции
экстремумы(локальные)функции
наибольшее и наименьшее значение функции
признаки вогнутости и выпуклости графиков, точки перегиба
неопределенный интерграл, свойства
основная таблица интегралов
метод непосредственного интегрирования
интегрирование по частям
замена переменной в неопределенном интеграле
интегральная сумма определенный интеграл, его геометрический смысл
свойства определенного интеграла
формула ньютона-лейбница
интегрирование по частям и замена переменной в опр. Интеграле
несобственные интегралы
дифференциальное уравнение первого порядка, их общее частное особое решение
задача коши, теорема сущ. Единственности решения задачи коши
уравнения с разделяющимися переменными
линейные уравнения первого порядка
дифф. Уравнения высших порядков, их общее и частной решение,задача коши
линейные диффер. Уравнения н-ого порядка,структура решения
линейные однородные дифф уравнения с постоянными коэф. Метод Эйлера
линейные неоднородные диф уравнения с правой частью специального вида. Метод неопр. Коэф
определение функции нескольких переменных, геометрическая интерпретация в возможных случаях предел и непрерывность
частное и полное приращение функции
частные производные
полный дифференциал
производная по направлению
градиент
локальный экстремум
абсолютный экстремум а хрен знает
условный экстремум
Основные понятия теория множеств
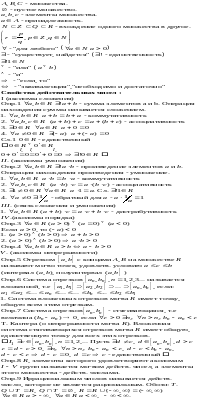
Операции над множествами
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Функция, ее область определения, способы задания Понятие функции одной переменной
Постоянной
величиной
называется величина, сохраняющая одно
и то же значение. Например, отношение
длины окружности к ее диаметру есть
постоянная величина, равная числу
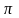 .
.
Если величина сохраняет постоянное значение лишь в условиях данного процесса, она называется параметром.
Переменной
называется величина, которая может
принимать различные числовые значения.
Например, при равномерном движении:
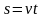 ,
где
,
где
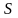 - путь,
- путь,
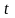 -
время,
-
время,
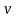 - параметр.
- параметр.
Определение.
Если каждому
элементу
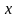 множества
множества
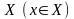 ставится в соответствие вполне
определенный элемент
ставится в соответствие вполне
определенный элемент
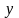 множества
множества
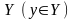 ,
то тогда говорят, что на множестве
,
то тогда говорят, что на множестве
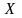 задана
функция
задана
функция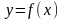 .
.
При этом
называется независимой переменной
(или аргументом),
- зависимой
переменной,
а буква
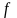 обозначает
закон соответствия.
обозначает
закон соответствия.
Множество
называется областью
определения
(или существования) функции, а множество
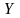 - областью
значений
функции.
- областью
значений
функции.
Если множество специально не оговорено, то под областью определения функции подразумевается область допустимых значений независимой переменной , т.е. множество таких значений , при которых функция вообще имеет смысл.
Способы задания функций:
а) Аналитический способ, если функция задана формулой вида . Этот способ наиболее часто встречается на практике.
Например,
функция
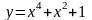 задана аналитически. Не следует, однако,
смешивать функцию с ее аналитическим
выражением. Так, например, одна функция
задана аналитически. Не следует, однако,
смешивать функцию с ее аналитическим
выражением. Так, например, одна функция
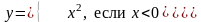 имеет два аналитических выражения:
имеет два аналитических выражения:
 (при
(при
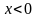 )
и
)
и
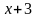 (при
(при
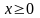 ).
).
б)
Табличный
способ
состоит в том, что функция задается
таблицей, содержащей значения аргумента
и соответствующие значения функции
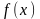 ,
например, таблица логарифмов, гармонические
функции и т.д.
,
например, таблица логарифмов, гармонические
функции и т.д.
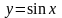 ,
,
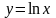 ,
,
 .
.
в)
Графический
способ
состоит в изображении графика функции
- множества точек
 плоскости, абсциссы которых есть значения
аргумента
,
а ординаты – соответствующие им значения
функции
.
плоскости, абсциссы которых есть значения
аргумента
,
а ординаты – соответствующие им значения
функции
.
г)
Словесный
способ,
если функция описывается правилом ее
составления, например, функция Дирихле:
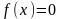 ,
если
-
иррационально.
,
если
-
иррационально.
Сложные и обратные функции
Сложная
функция, функция от функции.
Если величина y является функцией от u,
то есть у = f (u), а и, в свою очередь, функцией
от х, то есть u = j(х), то у является С. ф. от
х, то есть y = f [(x)], определённой для тех
значений х, для которых значения j(х)
входят в множество определения функции
f (u). В таком случае говорят, что у является
С. ф. независимого аргумента х, а u —
промежуточным аргументом. Например,
если у = u2, u = sinx, то у = sin2х для всех значений
х. Если же, например, у =
![]() ,
u = sinx, то у =
,
u = sinx, то у =
![]() , причём, если ограничиваться действительными
значениями функции, С. ф. у как функция
х
, причём, если ограничиваться действительными
значениями функции, С. ф. у как функция
х
![]() определена только для таких значений
х, для которых sin ³ 0, то есть для , где k
= 0, ± 1, ± 2,...
определена только для таких значений
х, для которых sin ³ 0, то есть для , где k
= 0, ± 1, ± 2,...
Производная
С. ф. равна произведению производной
данной функции по промежуточному
аргументу на производную промежуточного
аргумента по независимому аргументу.
Это правило (цепное правило) распространяется
на С. ф. с двумя, тремя и т. д. промежуточными
аргументами: если у = f (u1), u1 = j(u2),..., uk-1 =
jk-1(uk), uk = jk (x), то
![]()
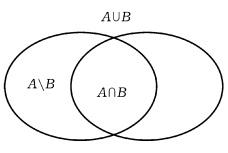
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
![]()
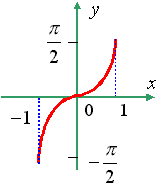
![]()
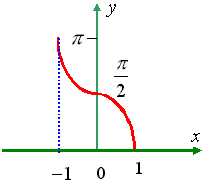
![]()