46. Линейные неоднородные диф уравнения с правой частью специального вида. Метод неопр. Коэф

метод неопределенных коэффициентов. Этот метод основывается на том, что многочлен -ой степени имеет ровно корней с учетом их кратности. Это означает, что если многочлен обращается в нуль более чем в точках, то этот многочлен нулевой (все коэффициенты равны нулю).

Запишем многочлены и с произвольными коэффициентами, т.е.

и

Умножим и сложим многочлены в левой части равенства:

получим

здесь приведены подобные, т.е. группировка по степеням .

В итоге получим, что для любого значения переменной выполняется равенство левой и правой частей. Это означает, что многочлен -ой степени обращается в нуль более, чем в точках. Для равенства нулю многочлена достаточно потребовать равенства нулю всех его коэффициентов.

Приравняем друг к другу коэффициенты при одинаковых степенях в равенстве

или

Имеем систему линейных алгебраических уравнений:

из которой определяются неизвестные коэффициенты.

47. Определение функции нескольких переменных, геометрическая интерпретация в возможных случаях предел и непрерывность

Определение. Если каждой паре (x,y) значений двух независимых переменных из области W ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y). z=f(x,y)

Геометрическое изображение функции двух переменных - поверхность.

Непрерывность функции нескольких переменных

Предел функции.

Пусть z=f(x,y) определена в некоторой окрестности A(x0,y0).

Определение. Постоянное число b называют пределом z=f(x,y) при P(x,y) стремящемся к A, если для любого e > 0 можно указать такое значение d > 0, что для всех x, удовлетворяющих неравенству |AP| < d, имеет место неравенство |f(x,y)-b| < e.

48. Частное и полное приращение функции

Частное и полное приращение функции.

Полное приращение функции Dz=f(x+Dx, y+Dy)-f(x,y)

Частное приращение функции Dx z=f(x+Dx)-f(x,y)

Dy z=f(x,y+Dy)-f(x,y)

Вообще, полное приращение функции не равно сумме частных приращений.

Пример. z=xy. Dx z=(x+Dx)y-xy=yDx

Dy z=x(y+Dy)-xy=xDy

Dz=(x+Dx)(y+Dy)-xy=yDx+xDy+DyDx № Dy z+Dx z

49. Частные производные Основные понятия. Частные производные

Определение. Пусть имеется переменных величин и каждому набору их значений из некоторого множества соответствует одно вполне определенное значение переменной величины из множества . тогда говорят, что задана функция нескольких переменных .

Переменные называются независимыми переменными или аргументами, - зависимая переменная. Множество называется областью определения функции, множество - областью значений функции.

Функцию двух переменных будем обозначать как .

Определение. Графиком функции двух переменных называется множество точек трехмерного пространства ( ), аппликата которых связана с абсциссой и ординатой функциональным соотношением . График представляет собой некоторую поверхность в трехмерном пространстве.

Частные производные функции двух переменных

Определение. Число 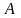называется пределом функции двух переменных в точке 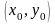, если для любого положительного числа существует положительное число , зависящее от , такое что для всех точек отстоящих от точки на расстоянии выполняется неравенство . Обозначение: .

Рассмотрим изменение функции при изменении только одной переменной, например, ; при этом другая переменная остается фиксированной

- частное приращение функции по переменной . Аналогично определяется частное приращение функции по переменной : .

Определение. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует).

Пусть , тогда , .

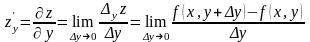Замечание. Так как частная производная функции 2-х переменных представляет собой обыкновенную производную функции одной переменной при постоянном значении другой переменной, то вычисляют частные производные по формулам и правилам дифференцирования функции одной переменной.

Пример. Найти частные производные функций а) , б) .

Решение. а) , . б) , .

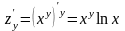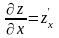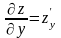Правило. Производная вычисляется при фиксированном значении , а производная вычисляется при фиксированном значении .

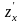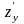Определение. Пусть функция имеет частные производные и , которые также являются функциями двух переменных и . Частные производные от этих функций называются частными производными второго порядка от функции . Каждая производная первого порядка имеет две частные производные. Таким образом, мы получаем 4 частные производные второго порядка, которые обозначаются следующим образом:

,	,
,	.

Определение. и называются смешанными производными функции .