Свойства дифференциала аналогичны свойствам производной.

1)	4)
2)	5)
3)

Инвариантность формы дифференциала

Если , то из (7.4) имеем .

Рассмотрим сложную функцию , где .

Если функции и дифференцируемые функции от своих аргументов, то производная сложной функции равна .

Умножим обе части равенства на : 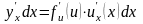. Таким образом, .

Это равенство означает, что формула дифференциала не изменится, если вместо функции от независимой переменной рассматривать функцию от зависимой переменной . Это свойство дифференциала получило название инвариантности (т.е. неизменности) формы дифференциала.

Приближенные вычисления с помощью дифференциала

Согласно формулы (7.1), , т.е. . При достаточно малых значениях приращение функции приблизительно равно ее дифференциалу

,

. (7.5)

Формула (7.5) часто используется в приближенных вычислениях.

Пример. Вычислить .

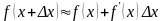Решение. Пусть . Найдем . Положим . В соответствии с (7.5) . Для функции имеем . .

21. Производные и дифференциалы высших порядков

Производные высших порядков. Бином Ньютона.

22. Теорема ферма

Для любого простого p и целого a, (a^p — a) делится на p.

Докажем, что для любого простого p и целого неотрицательного a, делится на p. Доказываем индукцией по a.

База. Для a=0, и делится на p.

Переход. Пускай утверждение верно для a=k. Докажем его для a=k+1.

Но делится на p по предположению индукции. Что же касается остальных слагаемых, то . Для , числитель этой дроби делится на p, а знаменатель — не делится, следовательно, делится на . Таким образом, вся сумма делится на p.

Для отрицательных a и нечётных p теорему легко доказать подстановкой b=-a. Для отрицательных a и p=2, истинность теоремы следует из

23. Теоремы роля, коши, Лагранжа

Теорема: (Коши о промежуточных значениях)

Пусть функция y=f(x) непрерывна на отрезке [a,b] и на концах принимает значение разные значения.

f(a)=A f(b)=B AB. Тогда С лежащею между А и В,  х₀(a,b): f(x₀)=C. Другими словами нет точек которые не являются значением отрезка.

Д оказательство: A<B, C(A,B) (x)=f(x)-C.

Эта функция непрерывна на отрезке [a,b]

(a)=f(a)-c=A-C<0 по теореме Коши №1  x₀(a,b):(x₀), то естьf(x₀)-C=0 f(x₀)=c

(b)=f(b)-c=B-C>0

Замечание: Условие непрерывности нельзя отбросить

[c,d][A,B]

[c,d)E(f)

Теорема Ролля. Пусть функция удовлетворяет следующим условиям:

1. непрерывна на отрезке ;

2. дифференцируема на интервале ;

3. на концах отрезка принимает разные значения, т.е. .

Т

огда внутри отрезка существует по крайней мере одна точка , в которой производная функции равна нулю: .

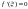Геометрический смысл теоремы Ролля. При выполнении условий теоремы внутри отрезка найдется точка , в которой касательная, проведенная к графику функции , параллельна оси (см. рис. 1). Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.

Замечание. Пусть . Тогда и – нули функции , и между ними найдется такая точка , что . Таким образом, из теоремы Ролля следует, что между нулями дифференцируемой функции находится хотя бы один нуль производной (см. рис. 2).

Теорема Роля является частным случаем теоремы Лагранджа.

Теорема Лагранжа. Пусть функция удовлетворяет следующим условиям:

1. непрерывна на отрезке ;

2. дифференцируема на интервале .

Тогда внутри отрезка существует по крайней мере одна точка , в которой выполняется равенство: .

Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.

Н

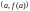а рис (см. рис. 3) хорда AB – отрезок, соединяющий точки и . Величина 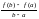равна тангенсу угла наклона прямой AB.

Геометрический смысл теоремы Лагранжа заключается в том, что при выполнении условий теоремы внутри отрезка найдется точка , в которой касательная, проведенная к графику функции , параллельна хорде AB. Таких точек может быть и несколько, но одна существует точно.

Следствие. При выполнении условий теоремы Лагранжа .

Эту формулу называют формулой конечных приращений.