29. Неопределенный интерграл, свойства Понятие первообразной и неопределенный интеграл

Определение. Функция называется первообразной функцией для функции на промежутке , если в каждой точке этого промежутка .

Пример. является первообразной для 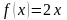, т.к. .

Можно заметить, что если для функции существует первообразная , то она не является единственной. Возвращаясь к примеру, видно, что и функции , и вообще ( - некоторое число) являются первообразными для функции . Таким образом можно сформулировать следующую теорему.

Теорема. Если и - первообразные для функции на некотором промежутке , то найдется такое число , что будет справедливо равенство:

.

Из данной теоремы следует, что, если - первообразная для функции , то выражение вида , где - произвольное число, задает все возможные первообразные для .

Определение. Совокупность всех первообразных функции на промежутке называется неопределенным интегралом от функции и обозначается , где - знак интеграла, - подынтегральная функция, - подынтегральное выражение.

Таким образом:

,

где - некоторая первообразная для , произвольная постоянная.

Определение. Операция нахождения неопределенного интеграла называется интегрированием этой функции.

Свойства неопределенного интеграла

1. Производная от неопределенного интеграла равна подынтегральной функции, т.е. .

□ Доказательство. Дифференцируя левую и правую части равенства , получаем: .■

2. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е. .

□ Доказательство. По определению дифференциала и свойству 1 имеем: ■

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е. .

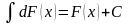□ Доказательство. Рассматривая функцию как первообразную для некоторой функции , можно записать: и на основании дифференциал неопределенного интеграла , откуда .■

4. Постоянный множитель можно выносить за знак интеграла, т.е. , где - некоторое число.

5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е. .

30. Основная таблица интегралов Некоторые табличные интегралы

,
,			,

31. Метод непосредственного интегрирования

Непосредственное интегрирование

Непосредственное интегрирование основано на свойстве 4 неопределенного интеграла Если функции f1(x), … fn(x) имеют первообразные в некотором промежутке, то функция f(x) = f1(x)+f2(x)+f3(x)+…+-fn(x) также имеет первообразную в том же промежутке, причем

т.е. неопределенный интеграл от суммы некоторого числа функций равен такой же сумме неопределенных интегралов от слагаемых.

32. Интегрирование по частям

Интегрирование - действие, обратное дифференцированию, то каждому правилу дифференцирования должно соответствовать некоторое правило интегрирования.

Пусть и - дифференцируемые функции от х. Имеем: , откуда .

Интегрируя обе части последнего равенства, получим: , или

.

Это и есть формула интегрирования по частям.

Интегрирование по частям состоит в том, что подынтегральное выражение представляется каким-либо образом в виде произведения двух множителей и (последний обязательно содержит ) и согласно формуле данное интегрирование заменяется двумя:

1) при отыскании из выражения для ;

2) при отыскании интеграла от .

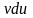Может оказаться, что эти два интегрирования легко осуществляются, тогда как заданный интеграл непосредственно найти трудно.

Правило интегрирования по частям нередко позволяет довести интегрирование до конца.

Пример. Найти .

Решение.