8.4.1. Умовний та безумовний екстремуми функції

У теорії дослідження функцій задача на відшукання екстремальних значень не містить ніяких додаткових умов щодо змінних і такі задачі належать до задач відшукання безумовного екстремуму функції. Локальний та глобальний екстремуми тоді визначаються з необхідних та достатніх умов існування екстремуму функції.

Нагадаємо, що необхідна умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб точка   була точкою локального екстремуму, необхідно, щоб функція   була неперервною і диференційовною в околі цієї точки і перші частинні похідні за змінними   та   у цій точці дорівнювали нулю:

.

Точка   називається критичною.

Достатня умова існування локального екстремуму функції двох змінних формулюється так: для того, щоб критична точка  була точкою локального екстремуму, достатньо, щоб функція   була визначена в околі критичної точки   та мала в цій точці неперервні частинні похідні другого порядку.

Тоді, якщо ,

то в точці   функція   має екстремум, причому, якщо

,

тоді   — точка локального максимуму функції  , а якщо

,

тоді   — точка локального мінімуму функції  .

У разі, якщо ,

то в точці   функція   екстремуму не має.

Якщо ,

то питання про існування екстремуму залишається відкритим.

Якщо задача полягає у відшуканні локального чи глобального екстремуму деякої функції за умови, що на змінні такої функції накладаються додаткові обмеження, то маємо задачу пошуку умовного екстремуму функції. Термін «умовний» означає, що змінні задачі мають задовольняти деякі умови.

Розглянемо таку задачу для випадку двох змінних:

знайти   (8.4)

за умови, що  . (8.5)

Найпростіший спосіб розв’язання задачі такого виду полягає в тому, що спочатку з обмеження (8.5) знаходять вираз однієї змінної через іншу. Приміром, визначають   через  . Отриманий вираз виду   підставляють у функцію (8.4), що після цього стає функцією однієї змінної  , і далі знаходять її безумовний екстремум.

Якщо деяка точка   є точкою екстремуму функції  , то точка   є точкою умовного екстремуму функції (8.4) за умови (8.5).

Однак не завжди вдається відшукати аналітичний вираз однієї змінної через іншу в умові (8.5). Часто це досить важко здійснити або неможливо. Також іноді складно узагальнити даний спосіб для функції n змінних, на які накладено m обмежень. Тому описана досить проста ідея зведення задачі відшукання умовного екстремуму функції кількох змінних до задачі на безумовний екстремум функції однієї змінної не може бути використана як основа універсального методу розв’язування задач на умовний екстремум. Цікавий метод розв’язування задач типу (8.4), (8.5) запропонував Лагранж.

Метод множників Лагранжа

Ідея методу множників Лагранжа полягає в заміні початкової задачі простішою. Для цього цільову функцію замінюють іншою, з більшою кількістю змінних, тобто такою, яка включає в себе умови, що подані як обмеження. Після такого перетворення дальше розв’язування задачі полягає в знаходженні екстремуму нової функції, на змінні якої не накладено ніяких обмежень. Тобто від початкової задачі пошуку умовного екстремуму переходимо до задачі відшукання безумовного екстремального значення іншої функції. Отже, завдяки такому перетворенню можливе застосування методів класичного знаходження екстремуму функції кількох змінних.

У попередньому параграфі наведена необхідна умова існування локального екстремуму неперервної та диференційовної функції двох змінних.

Узагальнення необхідної умови існування локального екстремуму функції n змінних має аналогічний вигляд. Отже, для розв’язування задачі необхідно знайти вирази частинних похідних нової цільової функції за кожною змінною і прирівняти їх до нуля. В результаті отримаємо систему рівнянь. Її розв’язок визначає так звані стаціонарні точки, серед яких є і шукані екстремальні значення функції.

Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:

 (8.6)

за умов:

, (8.7)

де функції   і   мають бути диференційовними.

Задача (8.6), (8.7) полягає в знаходженні екстремуму функції   за умов виконання обмежень  .

Переходимо до задачі пошуку безумовного екстремуму. В літературі [13, 28] теоретично доведено, що постановки та розв’язання таких задач еквівалентні.

Замінюємо цільову функцію (8.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:

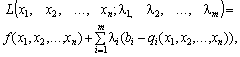 (8.8)

де   — деякі невідомі величини, що називаються множниками Лагранжа.

Знайдемо частинні похідні і прирівняємо їх до нуля:

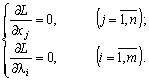
 (8.9)

Друга група рівнянь системи (8.9) забезпечує виконання умов (8.7) початкової задачі нелінійного програмування.

Система (8.9), як правило, нелінійна.

Розв’язками її є   і   — стаціонарні точки. Оскільки, ці розв’язки отримані з необхідної умови екстремуму, то вони визначають максимум, мінімум задачі (8.6), (8.7) або можуть бути точками перегину (сідловими точками).

Для діагностування стаціонарних точок і визначення типу екстремуму необхідно перевірити виконання достатніх умов екстремуму, тобто дослідити в околі стаціонарних точок диференціали другого порядку (якщо для функцій   існують другі частинні похідні і вони неперервні).

Узагальнення достатньої умови існування локального екстремуму для функції n змінних приводить до такого правила: за функцією Лагранжа виду (8.8) будується матриця Гессе, що має блочну структуру розмірністю  :

де О — матриця розмірністю  , що складається з нульових елементів,

Р — матриця розмірністю  , елементи якої визначаються так: ,

 — транспонована матриця до Р розмірністю  ,

Q — матриця розмірністю   виду:

, де  .

Розглянемо ознаки виду екстремуму розв’язку системи (8.9). Нехай стаціонарна точка має координати   і  .

1. Точка   є точкою максимуму, якщо, починаючи з головного мінору порядку (m + 1), наступні (n – m) головних мінорів матриці Нутворюють знакозмінний числовий ряд, знак першого члена якого визначається множником  .

2. Точка   є точкою мінімуму, якщо, починаючи з головного мінору порядку (m + 1), знак наступних (n – m) головних мінорів матриці Н визначається множником 

52.ПЕРЕРАХУВАТИ ОСНОВНІ ПОЛОЖЕННЯ,НА ПІДСТАВІ ЯКИХ ЗАВДАННЯ ПРО ПРИЗНАЧЕННЯ ЗВОДИТЬСЯ ДО ТРАНСПОРТНОГО ЗАВДАННЯ. Задача про призначення є частним випадком ТЗ.

Потрібно виконати n видів робіт, на які претендують n кандидатів. Витрати на оплату праці i-го кандидата за виконання j-ої роботи дорівнюють  . Кожен кандидат може бути призначений лише на одну роботу, і кожна робота має виконуватися лише одним кандидатом. Потрібно знайти оптимальне призначення кандидатів на виконання робіт, за якого сумарні витрати на виконання всіх робіт будуть мінімальними.

Має виконуватися умова:

. (5.5)

Транспортну задачу називають збалансованою, або закритою, якщо виконується умова (5.5). Якщо ж така умова не виконується, то транспортну задачу називають незбалансованою, або відкритою.

Якщо при перевірці виявилося,задача є відкритою,то її необхідно звести до закритого типу.Це здійснюється введенням фіктивного постачальника .

Домовимося планом транспортної задачі називати будь-який невід’ємний розв’язок системи обмежень (5.2)—(5.4), який позначають матрицею  . Значення невідомих величин  — обсяги продукції, що мають бути перевезені від i-х постачальників доj-х споживачів, називатимемо перевезеннями.

Задача про призначення може вирішуватись методом потенціалів(для ТЗ). Але оскільки змінні мають бульовий вигляд,тобто може мати 1 або 0,то використовується угорський метод.