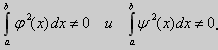- •Решение
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •Необходимый признак сходимости числового ряда.
- •Признак Даламбера
- •Свойства
- •Интегральный признак Коши сходимости числовых рядов
- •Признак Лейбница
- •Оценка остатка ряда Лейбница
- •Абсолютно сходящиеся ряды
- •Условно сходящиеся ряды с действительными членами
- •Степенной ряд
- •Разложение в ряд Фурье непериодических функций
Абсолютно сходящиеся ряды
Ряд с комплексными членами
![]() (1)
(1)
называется абсолютно сходящимся, если сходится ряд
![]() (2)
(2)
модулей его членов.
Абсолютно сходящийся ряд сходится.
В
самом деле, пусть ряд (1) абсолютно
сходится; тогда сходится ряд (2) и в силу
признака Коши для любого ![]() найдется
такое
найдется
такое ![]() ,
что
,
что ![]() для
всех
для
всех ![]() и
и ![]() .
Тем более, тогда
.
Тем более, тогда ![]() .
Поэтому, в силу признака Коши ряд (1)
сходится.
.
Поэтому, в силу признака Коши ряд (1)
сходится.
Сходящиеся
ряды с неотрицательными членами
тривиальным образом сходятся абсолютно.
Ряд ![]() сходится,
потому что он есть ряд Лейбница. Однако
абсолютно он сходится только при
сходится,
потому что он есть ряд Лейбница. Однако
абсолютно он сходится только при ![]() .
.
Условно сходящиеся ряды с действительными членами
Рассмотрим ряд
![]() (1)
(1)
с действительными членами сходящийся, но не абсолютно.
Можно
доказать, что, каково бы ни было число ![]() ,
конечное или бесконечное, т. е.
удовлетворяющее неравенствам
,
конечное или бесконечное, т. е.
удовлетворяющее неравенствам ![]() ,
существует перестановка членов ряда
(1), в результате которой получится ряд,
сходящийся к
.
Поэтому неабсолютно сходящиеся ряды
называют условно сходящимися.
,
существует перестановка членов ряда
(1), в результате которой получится ряд,
сходящийся к
.
Поэтому неабсолютно сходящиеся ряды
называют условно сходящимися.
Степенной ряд. Теорема Абеля о структуре области сходимости степенного ряда. Радиус сходимости.
Степенной ряд
Рассмотрим степенной ряд
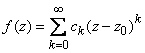
![]() ,
(1)
,
(1)
имеющий
радиус сходимости ![]() .
.
Из
теории степенных рядов мы знаем, что
ряд (1) равномерно сходится на круге ![]() ,
где
,
где ![]() -
любое положительное число, меньшее
-
любое положительное число, меньшее ![]() .
Поэтому сумма
.
Поэтому сумма ![]() ряда
(1) - непрерывная функция в открытом
круге
ряда
(1) - непрерывная функция в открытом
круге ![]() .
Больше того,
имеет
на этом круге непрерывную производную
.
Больше того,
имеет
на этом круге непрерывную производную ![]() любого
порядка, которую можно вычислить путем
почленного дифференцирования ряда (1).
Это показывает, что сумма степенного
ряда есть аналитическая функция в круге
(открытом!) его сходимости. Числа
любого
порядка, которую можно вычислить путем
почленного дифференцирования ряда (1).
Это показывает, что сумма степенного
ряда есть аналитическая функция в круге
(открытом!) его сходимости. Числа ![]() вычисляются
по формуле
вычисляются
по формуле
![]()
![]() ,
(2)
,
(2)
что показывает, что степенной ряд есть ряд Тейлора своей суммы эту формулу можно заменить следующей:
![]() ,
,
где ![]() -
произвольный контур, ориентированный
против часовой стрелки, принадлежащий
к кругу сходимости ряда (1) и содержащий
внутри точку
-
произвольный контур, ориентированный
против часовой стрелки, принадлежащий
к кругу сходимости ряда (1) и содержащий
внутри точку ![]() .
.
Правило разложения функции в степенной ряд. Формулы Маклорена для коэфицентов.
Если
функция ![]() в
некотором интервале раскладывается в
степенной ряд по степеням
в
некотором интервале раскладывается в
степенной ряд по степеням ![]() ,
то это разложение единственно и задается
формулой:
,
то это разложение единственно и задается
формулой:
![]()
Формулы Маклорена некоторых элементарных функций.
1) f(x)=e^x
f '(x)=f "(x)=…=f(n+1)(x)=e^x
f(0)=f '(0)=f "(0)=…=f(n+1)(0)=1
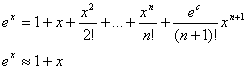 (5)
(5)
2) f(x)=sinx

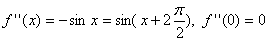
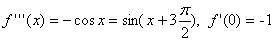


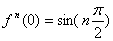
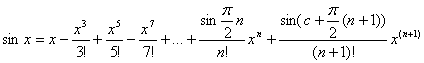 (6)
(6)
3) f(x)=cosx
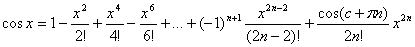 (7)
(7)
Формула Логранжа для остатка степенного ряда. Приближенное вычисление «е».
Формула Тейлора
Формула Тейлора

(Rn(x) - остаточный член формулы Тейлора).
Остаточный член формулы Тейлора
В форме Лагранжа:
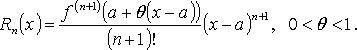
Применение степенных рядов в приближенных вычислениях и решениях дифферинциальных уравнений
Применение рядов к приближённым вычислениям |
Числовые и функциональные ряды широко применяются в приближённых вычислениях. Рассмотрим это на примерах.
Пример 1.
Вычислить
Воспользуемся
разложением
= Так как ряд знакочередующийся и 0,0008<0,001, то все слагаемые, начиная с 0,0008, отбрасываем и при этом погрешность не превосходит 0,001.
Пример 2.
Вычислить
=
≈2(1+
+ Так как, начиная со второго члена, ряд знакочередующийся и 0,00096<0,001, то все слагаемые, начиная с 0,00096, отбрасываем и при этом погрешность не превосходит 0,001. |
Какие функции называются ортогональными на отрезке? Тригонометрическая система.
Две функции φ(x) и ψ(x) называются ортогональными на отрезке[a,b] (или в интервале (a,b)),если
![]()
При этом предполагается, что |
|
Система функций {φn(x),n=0,1,2, ... }- ортогональна на отрезке [a,b] (или в интервале (а,b)),если
![]()
Здесь тоже предполагается, что |
|
Иными словами,система функций {φn(x), n = 0, 1, 2, ...} ортогональна на отрезке [a,b], если все функции попарно ортогональны. Число

называется нормой функции φn(x). Если все функции φn(x) имеют единичную норму и система ортогональна на [a,b], то такая система функций называется ортонормированной.
Простейшим примером ортогональной системы функций служит тригонометрическая система
{1, sinx, cosx, sin 2x, cos 2x, ... , sin nx, cos nx, ...} |
|
ТРИГОНОМЕТРИЧЕСКАЯ СИСТЕМА
одна
из важнейших ортогональных
систем функций.
Функции Т. с. 1, cosx, sinx,
. ..,cosnx,sinnx,
. .. ортогональны
на любом отрезке вида ![]() а
функции
а
функции
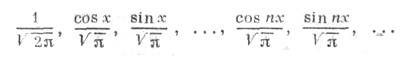
ортонормированы
на этом отрезке. Т. с. полна и замкнута
в пространстве ![]() при
при ![]() а
также в пространстве
а
также в пространстве ![]() непрерывных
непрерывных ![]() -периодических
функций. Эта система образует базис в
пространстве
-периодических
функций. Эта система образует базис в
пространстве ![]()
![]() при
при ![]() Ряды
по Т. с. изучаются в теории тригонометрических
рядов.
Наряду
с Т. с. широкое применение находит
комплексная тригономстрич. система
Ряды
по Т. с. изучаются в теории тригонометрических
рядов.
Наряду
с Т. с. широкое применение находит
комплексная тригономстрич. система ![]() Функции
этих систем связаны друг с другом
формулами Эйлера.
Функции
этих систем связаны друг с другом
формулами Эйлера.
Правило разложения функций в ряд Фурье. Теорема Дирихле.
Разложить
в ряд Фурье функцию (периода ![]() )
) ![]() .
.
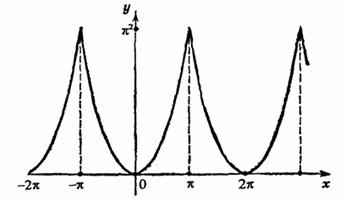
Рис. 116
Данная
функция четная. Тогда ее ряд Фурье
состоит только из косинусов ![]() .
Вычислим коэффициенты
.
Вычислим коэффициенты ![]() :
:
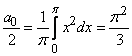
и

Таким образом,
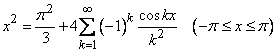 .
.
Теорема Дирихле.
Распределение
тепла в теле называется стационарным,
если температура ![]() тела
зависит от положения точки
тела
зависит от положения точки ![]() ,
но не зависит от времени
,
но не зависит от времени ![]() ,
т. е.
,
т. е.
![]() .
.
В этом случае
![]()
и функция удовлетворяет уравнению
![]() .
.
Определение.
Функция ![]() называется
гармонической на области
называется
гармонической на области ![]() ,
если она имеет непрерывные частные
производные второго порядка на
и
удовлетворяет на
уравнению
,
если она имеет непрерывные частные
производные второго порядка на
и
удовлетворяет на
уравнению
. (1)
Уравнение (1) называется уравнением Лапласа. Справедлива
Теорема
1. Пусть ограниченная область
пространства
имеет кусочно-гладкую границу
(поверхность) ![]() ,
на которой задана непрерывная функция
,
на которой задана непрерывная функция ![]() .
Тогда существует на замыкании
.
Тогда существует на замыкании ![]() единственная
непрерывная функция
,
гармоническая на
,
такая, что
единственная
непрерывная функция
,
гармоническая на
,
такая, что
![]() .
.
Теорема 1 имеет очевидную физическую интерпретацию. Если на границе тела все время поддерживать температуру , равную , где - заданная непрерывная на функция, то внутри тела установится вполне определенная (единственная) температура . Это утверждение с физической точки зрения надо считать очевидным. Но оно может быть доказано и математически. Эта задача, называемая задачей Дирихле, исследована очень хорошо, при этом даются различные приближенные методы ее решения.
Задача Дирихле имеет большое практическое применение и в плоском случае. В плоском случае она формулируется так.
На
кусочно-гладкой границе
плоской
области
задана
непрерывная функция ![]() .
Требуется найти функцию
.
Требуется найти функцию![]() ,
непрерывную на
,
непрерывную на ![]() и
гармоническую на
,
т. е. имеющую вторые непрерывные частные
производные и удовлетворяющую уравнению
Лапласа на
:
и
гармоническую на
,
т. е. имеющую вторые непрерывные частные
производные и удовлетворяющую уравнению
Лапласа на
:
 .
.
Эта задача решается положительно: на существует и притом единственная функция , удовлетворяющая требованиям этой задачи.
Особенно важны те случаи, когда задача Дирихле решается эффективно.
Ряд Фурье для четных и не четных функций!
Пусть f(x) - четная функция с периодом 2L, удовлетворяющая условию f(-x) = f(x) .
Тогда для коэффициентов ее ряда Фурье находим формулы:
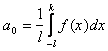 =
=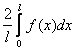
 =
=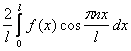
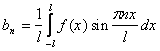 =
0
=
0![]() ,
где n=1,2,
...
,
где n=1,2,
...
Таким образом, в ряде Фурье для четной функции отсутствуют члены с синусами, и ряд Фурье для четной функции с периодом 2Lвыглядит так:
![]()
Пусть теперь f(x) - нечетная функция с периодом 2L, удовлетворяющая условию f(-x) = - f(x).
Тогда для коэффициентов ее ряда Фурье находим формулы:
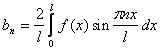 ,
где n=1,2,
...
,
где n=1,2,
...
Таким образом, в ряде Фурье для нечетной функции отсутствует свободный член и члены с косинусами, и ряд Фурье для нечетной функции с периодом 2L выглядит так:
![]()
Если
функция f(x)
разлагается в тригонометрический ряд
Фурье на промежутке![]() то
то ![]()
,
где
 ,
,
 ,
,
 ,
,
Если f(x) разлагается в тригонометрический ряд Фурье на [0,L], то доопределив заданную функцию f(x) соответствующим образом на [-L,0]; далее периодически продолжив на (T=2L), получим новую функцию, которую разлагаем в тригонометрический ряд Фурье.
Для разложения в ряд Фурье непериодической функции, заданной на конечном произвольном промежутке [a,b], надо : доопределить на [b,a+2L] и периодически продолжить, либо доопределить на [b-2L,a] и периодически продолжить.

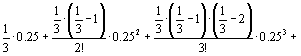
 2.(1+0,0833--0,0069+0,00096)
≈
≈2.(1+0,0833-0,0069)
≈2,1528≈2,153.
2.(1+0,0833--0,0069+0,00096)
≈
≈2.(1+0,0833-0,0069)
≈2,1528≈2,153.