Выполнил: студент гр. ЭУМ-31 Чекин Д.Г.

Вариант 10.

Решение.

1. Построим поле корреляции и сформулируем гипотезу о форме связи.

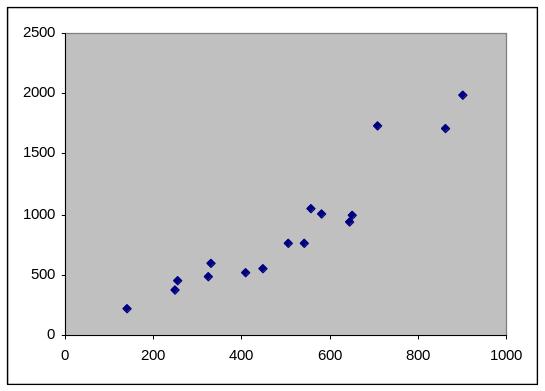
Н₀ – гипотеза о случайной природе оцениваемых характеристик;

Н₁ – гипотеза о статистической значимости и надежности уравнения регрессии.

2. Рассчитаем параметры уравнений парной регрессии (n=16).

1. Линейная y=a + b*x (оставляем 2 знака после запятой)

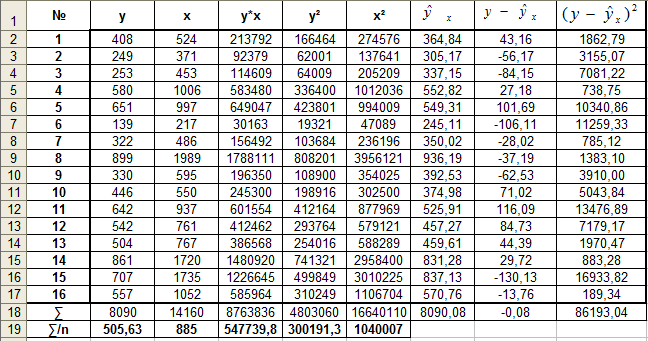
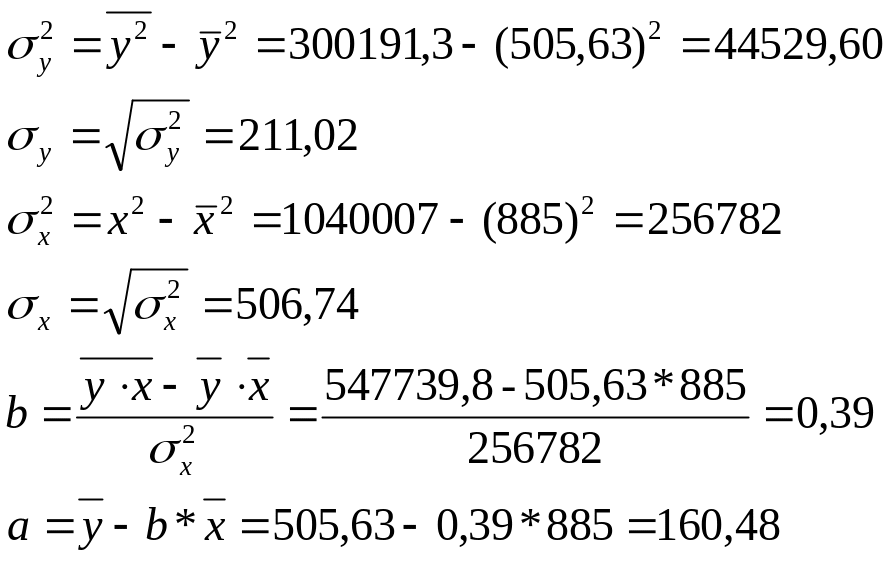
Уравнение линейной регрессии:

Вывод: С увеличением средней заработанной платы и выплаты социального характера (x) на 1 тыс.руб. потребительские расходы на душу населения (y) повышаются (так как b=0,39 >0) в среднем на 0,39 тыс. руб.

y – значение потребительских расходов на душу населения, полученное эмпирическим (опытным) путем;

- значение потребительских расходов на душу населения, полученное теоретическим путем.

Б. Степенная

Логарифмируем обе части уравнения: Y=A+b*X, где

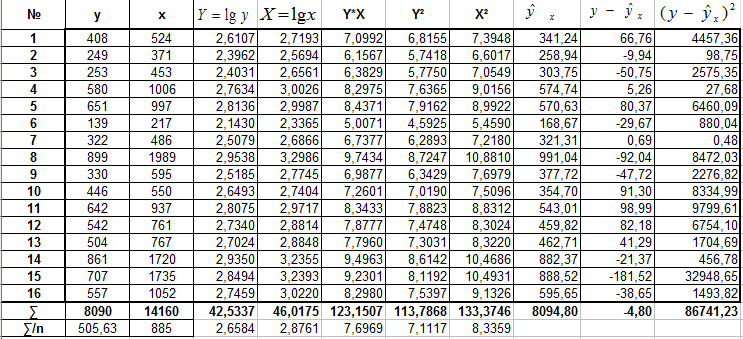
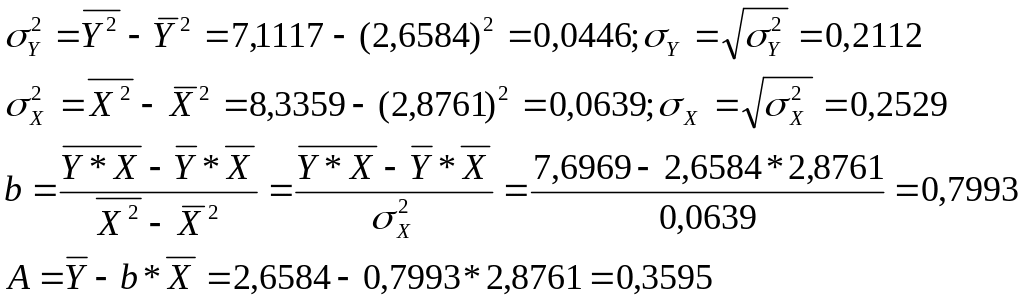
Получим линейное уравнение:

В ыполнив его потенцирование, получим:

Уравнение степенной регрессии:

В. Экспоненциальная

Логарифмируем обе части уравнения: ln y = a+b*x, Y = a+b*x, где Y = ln y.

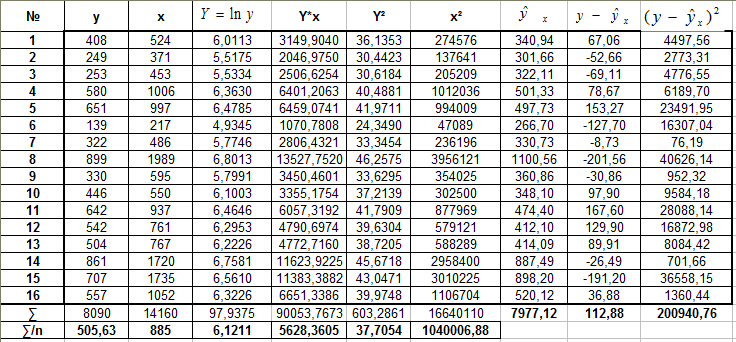
Получим

Получим линейной уравнение:

В ыполнив его потенцирование, получим:

Уравнение экспоненциальной регрессии:

Г. Полулогарифмическая

Положим X = lnx, тогда уравнение примет вид y=a+b*X.

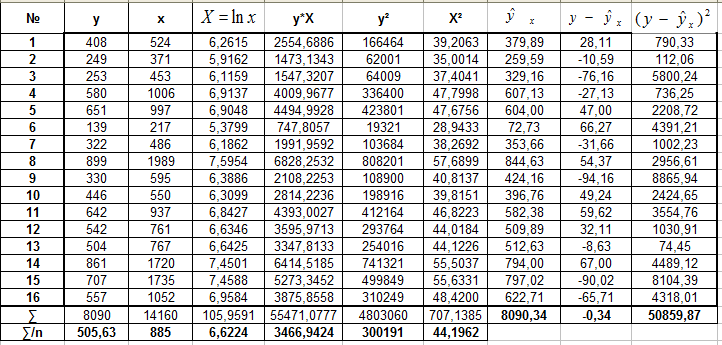
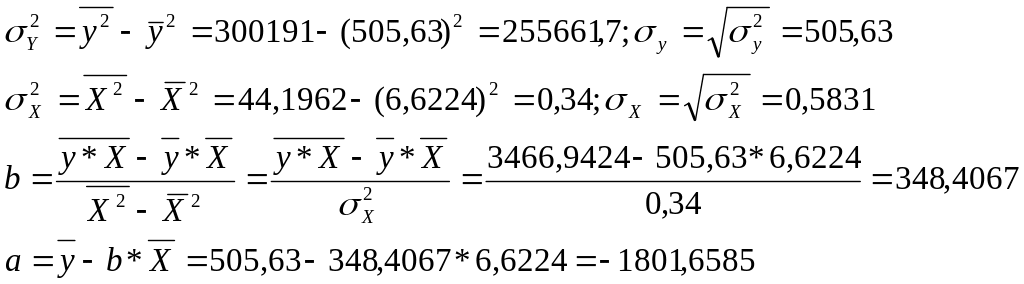
Получим линейное уравнение: .

Уравнение полулогарифмической регрессии:

Д. Обратная (или 1/y=a+b*x).

Положим z=1/y, тогда уравнение примет вид z=a+b*x.

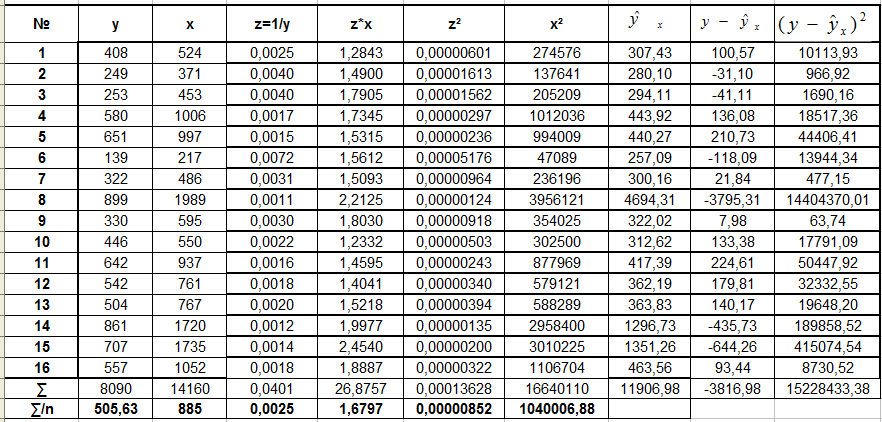
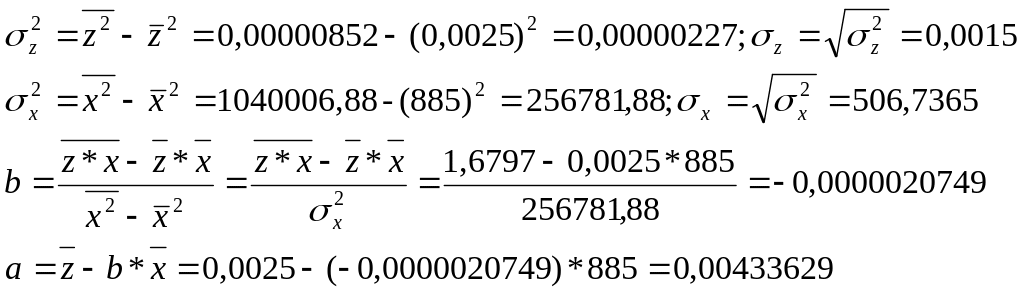
Уравнение обратной регрессии:

Е. Гиперболическая

Положим z=1/x, тогда уравнение примет вид y=a+b*z.

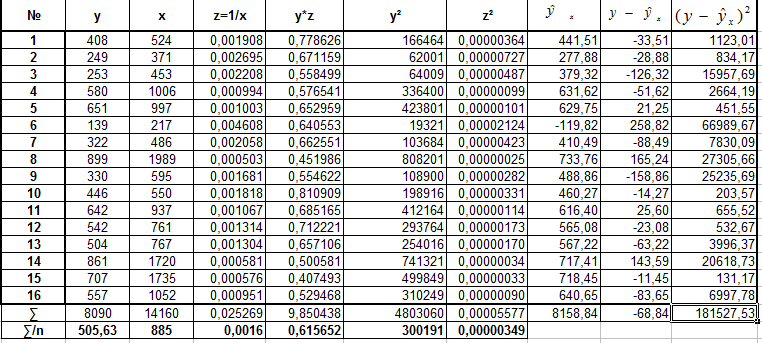
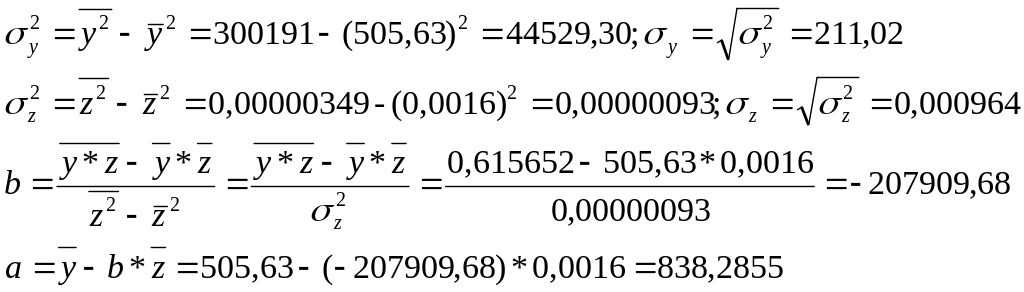
Получим линейное уравнение:

Уравнение гиперболической регрессии:

3. Оценим тесноту связи с помощью показателей корреляции и детерминации (для каждого уравнения).

А. Для линейной регрессии

Коэффициент корреляции

Так как , то линейная связь между x и y характеризуется как сильная (тесная).

Коэффициент детерминации равен , то есть 87,71 % вариации (разброса) зависимой переменной (y) объясняется линейной регрессией.

Б. Для степенной регрессии

Индекс корреляции .

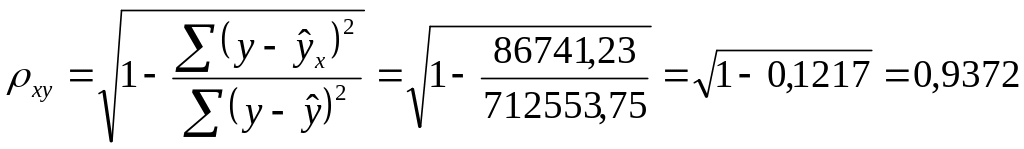Так как , то степенная связь между x и y характеризуется как сильная (тесная).

Индекс детерминации , то есть 87,83% вариации (разброса) зависимой переменной (y) объясняется степенной регрессией.

В. Для экспоненциальной регрессии .

Индекс корреляции

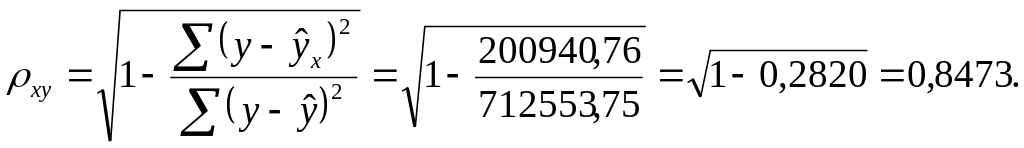
Так как , то экспоненциальная связь между x и y характеризуется как сильная (тесная).

Индекс детерминации , то есть 71,08 % вариации (разброса) зависимой переменной (y) объясняется экспоненциальной регрессией.

Г. Для полулогарифмической регрессии

Индекс корреляции

Так как , то полулогарифмическая связь между x и y характеризуется как сильная.

Индекс детерминации , то есть 92,86 % вариации (разброса) зависимой переменной (y) объясняется полулогарифмической регрессией.

Д. Для обратной регрессии

Индекс корреляции

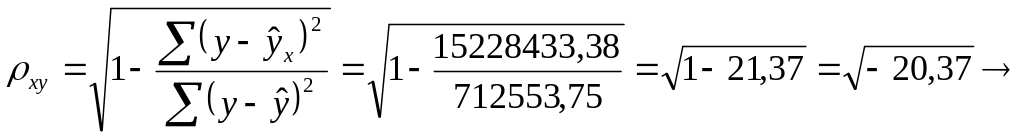
Между случайными величинами X и Y нет нелинейной связи.

Е. Для гиперболической регрессии

Индекс корреляции

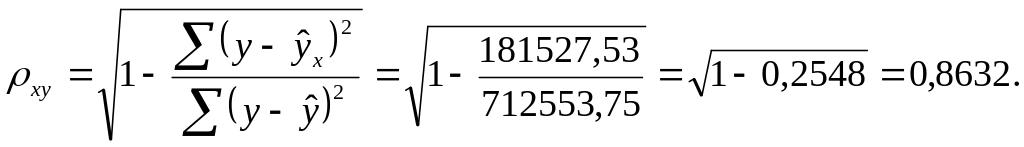
Так как , то полулогарифмическая связь между x и y характеризуется как сильная.

Индекс детерминации , то есть 74,52 % вариации (разброса) зависимой переменной (y) объясняется полулогарифмической регрессией.

Вывод: На основании значений показателя детерминации R² для каждого уравнения регрессии видим, что наилучшим образом описывает взаимосвязь между средней заработанной платой и выплатами социального характера (x) и потребительскими расходами на душу населения (y) полулогарифмическое уравнение регрессии (R² = 0,9286>0,7).

4. Дадим сравнительную оценку силы связи фактора (X) с результатом (y) с помощью среднего (общего) коэффициента эластичности:

Эластичность показывает, на сколько процентов изменяется функция y = f(x) при изменении независимой переменной x на 1 %.

А. Для линейной регрессии y = a+b*x ( ),

%

Б. Для степенной регрессии ( ),

%

В. Для экспоненциальной регрессии ( ),

%

Г. Для полулогарифмической регрессии ( )

%

Д. Для обратной регрессии ( )

Е. Для гиперболической регрессии ( ),

%

Вывод: На основании значений модуля коэффициента эластичности для каждого уравнения регрессии видим, что наибольшее значение коэффициента эластичности имеет уравнение степенной регрессии ( .

Он показывает, что с увеличением средней заработанной платы и выплат социального характера (x) на 1 % потребительские расходы на душу населения (y) возрастут (т.к в среднем на 0,7993 %.

5. Оценим статистическую значимость параметров линейной регрессии и коэффициента корреляции с помощью t-критерия Стьюдента (a, b, rxy).

Уравнение линейной регрессии y = a+b*x ( ),

n – общее число наблюдений (n=16);

H₀ - гипотеза о статистической незначимости параметров (о равенстве их нулю).

Вычислим случайные ошибки параметров линейной регрессии и коэффициента корреляции:

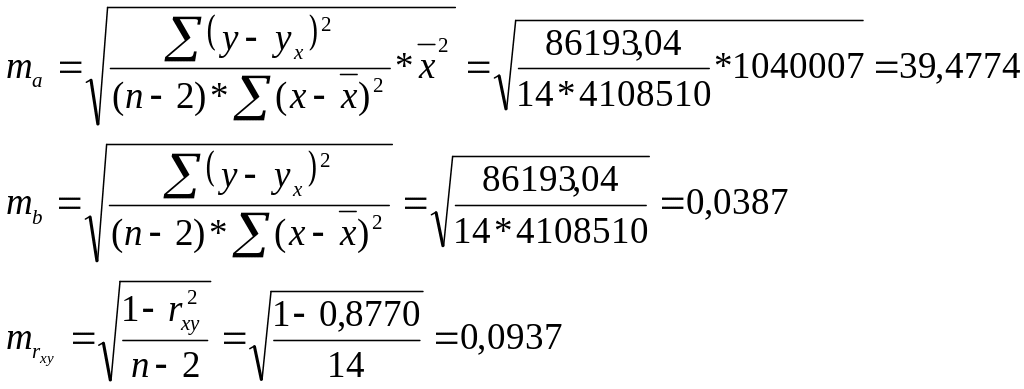
Сопоставим их значения со значениями параметров:

По таблице критических точек распределения Стьюдента, по заданному уровню значимости =0,05 и числу степеней свободы k=n-2 = 16-2 = 14 определим t_кр для двусторонней критической области: t_кр = 2,1448

Вывод:

Так как то гипотеза H₀ отвергается, т.е. параметр a для уравнения линейной регрессии является статистически значимым.

Так как то гипотеза H₀ отвергается, т.е. параметр b для уравнения линейной регрессии является статистически значимым.

Так как то гипотеза H₀ отвергается, т.е. коэффициент корреляции r_xy для уравнения линейной регрессии является статистически значимым.

Предельные ошибки для параметров a и b:

Доверительные интервалы имеют вид:

для параметра a – (a - ∆_a ; a + ∆_a ) или (160,48 – 84,6711; 160,48+84,6711) = (75,8089; 245,1511)

для параметра b – (b - ∆_b ; b + ∆_b ) или (0,39 – 0,0830; 0,39 + 0,0830) = (0,307; 0,473).

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. являются статистическими значимыми и существенно отличаются от нуля.