
- •Решение
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •Необходимый признак сходимости числового ряда.
- •Признак Даламбера
- •Свойства
- •Интегральный признак Коши сходимости числовых рядов
- •Признак Лейбница
- •Оценка остатка ряда Лейбница
- •Абсолютно сходящиеся ряды
- •Условно сходящиеся ряды с действительными членами
- •Степенной ряд
- •Разложение в ряд Фурье непериодических функций
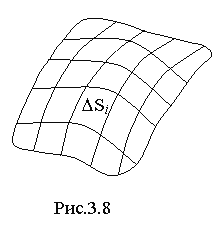
Рассмотрим
на плоскости или в пространстве кривую
L и функцию f, определенную в каждой точке
этой кривой. Разобьем кривую на части
Δsi длиной Δsi и выберем на каждой из
частей точку Mi. Составим интегральную
сумму ![]() .
Назовем λ длину наибольшего отрезка
кривой.
.
Назовем λ длину наибольшего отрезка
кривой.
Определение 10.1. Если существует конечный предел интегральной суммы , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi, то он называется криволинейным интегралом первого рода от функции f по кривой L и обозначается
![]() .
(10.1)
.
(10.1)
Например, если функция f(M) задает плотность в точке М, то интеграл (10.1) равен массе рассматриваемой кривой.
Свойства криволинейного интеграла 1-го рода.
Если функция f непрерывна на кривой L, то интеграл
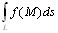 существует.
существует.Криволинейный интеграл 1-го рода не зависит от направления движения по кривой, то есть от того, какую из точек, ограничивающих кривую, считать начальной, а какую – конечной. Если назвать эти точки А и В, то
![]() (10.2)
(10.2)
Справедливость этих свойств следует из определения криволинейного интеграла 1-го рода.
Способ вычисления криволинейного интеграла 1-го рода.
Выберем
на кривой L направление от начальной
точки А и отметим, что положение точки
М на кривой определяется длиной дуги
АМ = s. Тогда кривую L можно задать
параметрически: x = x(s), y = y(s), z = z(s),
где ![]() Функция
f(x,y,z) становится при этом сложной функцией
одной переменной s: f(x(s), y(s), z(s)). Тогда
интегральная сумма
Функция
f(x,y,z) становится при этом сложной функцией
одной переменной s: f(x(s), y(s), z(s)). Тогда
интегральная сумма
![]() ,
,
где ![]() -
координата точки Mi, является обычной
интегральной суммой для определен-ного
интеграла
-
координата точки Mi, является обычной
интегральной суммой для определен-ного
интеграла ![]() Следовательно,
Следовательно,
= (10.3)
Если же кривая L задана в параметрической форме:
x = φ(t), y = ψ(t), z = χ(t), t0 ≤ t ≤ T,
то, применяя в интеграле (10.3) формулу замены переменной и учитывая, что дифференциал дуги
![]()
получим:
![]() (10.4)
(10.4)
Таким образом, вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции переменной t в пределах, соответствующих изменению значения этой переменной на рассматриваемой кривой.
Пример.
Вычислить ![]() где
L:
где
L: 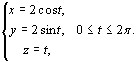 Применяя
формулу (10.4), получим:
Применяя
формулу (10.4), получим:
![]()
![]()
Криволинейный интеграл второго рода.
Вновь
рассмотрим кривую L, в каждой точке
которой задана функция f(M), и зададим
разбиение кривой на отрезки. Выберем
на каждом отрезке точку Mi и умножим
значе-ние функции в этой точке не на
длину i-го отрезка, как в случае
криволинейного инте-грала 1-го рода, а
на проекцию этого отрезка, скажем, на
ось Ох, то есть на разность xi
– xi-1 = Δxi. Составим из полученных
произведений интегральную сумму ![]() .
.
Определение
10.2. Если существует конечный предел
при ![]() интегральной
суммы
,
не зависящий от способа разбиения кривой
на отрезки и выбора точек Mi, то от
называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается
интегральной
суммы
,
не зависящий от способа разбиения кривой
на отрезки и выбора точек Mi, то от
называется криволинейным интегралом
второго рода от функции f(M) по кривой L
и обозначается
![]() .
(10.5)
.
(10.5)
Подобным образом можно определить и криволинейные интегралы 2-го рода вида
![]()
Определение 10.3. Если вдоль кривой L определены функции P(M) = P(x, y, z),
Q(M) = Q(x, y, z), R(M) = R(x, y, z) и существуют интегралы
![]() ,
,
то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают
![]()
![]() .
(10.6)
.
(10.6)
Замечание.
Если считать, что сила ![]() действует
на точку, движущуюся по кривой (АВ), то
работа этой силы может быть представлена
как
действует
на точку, движущуюся по кривой (АВ), то
работа этой силы может быть представлена
как
![]() ,
,
то есть криволинейным интегралом 2-го рода.
Свойства криволинейного интеграла 2-го рода.
Если функции P(M), Q(M), R(M) непрерывны на кривой (АВ), то интеграл (10.6) существует (справедливость этого утверждения следует из определения 10.2).
При изменении направления кривой (то есть перемены местами начальной и конечной ее точек) криволинейный интеграл 2-го рода меняет знак:
![]() (10.7)
(10.7)
Действительно, при этом изменяется знак Δxi в интегральной сумме.
Способ вычисления криволинейного интеграла 2-го рода.
Теорема 10.1. Пусть кривая L задана параметрическими уравнениями
x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β ,
где φ, ψ, χ – непрерывно дифференцируемые функции, и на ней задана непрерывная функция f(x, y, z). Тогда интеграл (10.5) существует и имеет место равенство
![]() .
(10.8)
.
(10.8)
Доказательство.
Запишем Δxi = xi – xi-1 = φ(ti) – φ(ti-1) и преобразуем последнюю разность по формуле Лагранжа: φ(ti) – φ(ti-1) = φ΄(τi)Δti, где τi – некоторое значение t, заключенное между ti-1 и ti. Выберем точку Мi так, чтобы ее координаты соответствовали значению параметра, равному τi : Mi(φ(τi), ψ(τi), χ(τi)). Подставив эти значения в формулу (10.5), получим:
![]() .
.
Справа получен предел интегральной суммы для функции f(φ(t),ψ(t),χ(t))φ΄(t) на отрезке [α, β], равный определенному интегралу от этой функции:
,
что и требовалось доказать.
Следствие.
Аналогичные соотношения можно получить
для криволинейных интегра-лов вида ![]() ,
откуда следует, что
,
откуда следует, что
![]()
![]() (10.9)
(10.9)
Пример.
Вычислим
интеграл ![]() ,
где L – отрезок прямой от точки А(1,2,-2)
до точки В(0, -1, 0). Запишем уравнение этой
прямой в параметрическом виде:
,
где L – отрезок прямой от точки А(1,2,-2)
до точки В(0, -1, 0). Запишем уравнение этой
прямой в параметрическом виде:
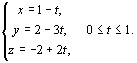
Следовательно, φ΄(t) = -1, ψ΄(t) = -3, χ΄(t) = 2. Тогда
![]()
![]()
Поверхностный интеграл первого рода |
|
|
Скалярное поле. Производная по направлению. Градиент |
Пусть
в пространстве Oxyz имеется
область D,
в которой задана функция Рассмотрим
точки области D,
в которых функция поля имеет постоянное
значение C: Наряду
со скалярными полями в пространстве
рассматривают также плоские скалярные
поля. Функция плоского скалярного
поля имеет вид П Рассмотрим
точку Производной
функции
в
точке P по
направлению
(обозначают Заметим:
если По
условию функция
дифференцируема,
значит, ее полное приращение можно
представить в виде Перейдем
к пределу при Если
направление
совпадает
с направлением какой–либо из осей
координат, то
совпадает
с соответствующей частной производной.
Пусть, например, луч
направлен
по оси Oy.
Тогда Для
плоского скалярного поля Градиентом скалярного
поля, заданного дифференцируемой
функцией
,
называется вектор, координаты которого
совпадают со значениями соответствующих
частных производных этой функции:
Таким образом, gradu есть вектор, указывающий направление наибольшего возрастания поля в данной точке и имеющий модуль, равный скорости этого возрастания. |
Векторное поле.
Векторное
поле в пространстве задается в каждой
точке ![]() с
помощью вектора
с
помощью вектора
![]() ,
,
где
проекции ![]() являются
функциями точки
являются
функциями точки ![]() .
.
Если
поверхность ![]() в
пространстве задана уравнением
в
пространстве задана уравнением ![]() ,
то единичный вектор нормали
,
то единичный вектор нормали ![]() к
этой поверхности равен
к
этой поверхности равен
 (1)
(1)
Знак берется в зависимости от выбранной стороны двусторонней поверхности .
Потоком
векторного поля ![]() через
поверхность
называется
поверхностный интеграл
через
поверхность
называется
поверхностный интеграл
![]() ,
где
,
где ![]() – единичный вектор нормали в произвольной
точке
– единичный вектор нормали в произвольной
точке ![]() .
.
Если
однозначно
проектируется на плоскость XOY в
область ![]() ,
то вычисление потока сводится к вычислению
двойного интеграла по
:
,
то вычисление потока сводится к вычислению
двойного интеграла по
:
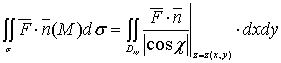 ,
(3)
,
(3)
где ![]() есть
коэффициент при
есть
коэффициент при ![]() для
вектора
,
а
для
вектора
,
а ![]() получается
из уравнения поверхности.
получается
из уравнения поверхности.
Аналогично можно проектировать на плоскость YOZ или ZOX.
Другой способ вычисления потока состоит в проектировании поверхности на все три координатные плоскости, если проектируется на них однозначно, т.е.
![]() ,
(4)
,
(4)
где
знаки перед интегралами совпадают со
знаками ![]() для
вектора
для
вектора ![]() ,
а функции
сведены
к двум переменным с помощью уравнения
поверхности.
,
а функции
сведены
к двум переменным с помощью уравнения
поверхности.
Для
вычисления потока через внешнюю сторону
замкнутой поверхности ![]() удобно применить формулу Остроградского
– Гаусса:
удобно применить формулу Остроградского
– Гаусса:
![]() ,
(5)
,
(5)
где  –
дивергенция векторного поля
в
точке
.
–
дивергенция векторного поля
в
точке
.
Поток
будет равен тройному интегралу от ![]() ,
взятому по объему
,
взятому по объему ![]() ,
ограниченному поверхностью
.
,
ограниченному поверхностью
.
Если
в пространстве задано векторное поле
и
линия ![]() ,
то работа этого поля вдоль линии
,
то работа этого поля вдоль линии ![]() представляет собой криволинейный
интеграл
представляет собой криволинейный
интеграл ![]()
Циркуляцией векторного поля называется криволинейный интеграл этого поля вдоль замкнутого пути :
![]() (6)
(6)
При вычислении этот интеграл сводится к определенному интегралу с помощью уравнения линии .
Если
линия
разделена
на части ![]() и
и ![]() ,
то интеграл
,
то интеграл ![]()
Поток векторного поля через ориентированную поверхность
Поток
векторного поля.
Рассмотрим кусок поверхности ![]() ,
заданной уравнением
,
заданной уравнением ![]() .
Пусть выполняется условие
.
Пусть выполняется условие ![]() ,
что означает, что в каждой точке
поверхности существует нормаль с
направляющим вектором
,
что означает, что в каждой точке
поверхности существует нормаль с
направляющим вектором ![]() .
Выберем одну из сторон поверхности
следующим образом: построим на поверхности
достаточно малый замкнутый контур, на
котором задано направление обхода.
Построим вектор нормали в точке
поверхности, лежащей внутри контура.
Если из конца вектора нормали обход
контура кажется происходящим против
часовой стрелки, то будем называть
сторону поверхности, обращенную к
вектору нормали положительной стороной.
Таким образом, будем рассматривать
ориентированную двухстороннюю
поверхность, а односторонние поверхности
лист Мебиуса, бутылку Клейна оставим в
покое. Потоком векторного поля
.
Выберем одну из сторон поверхности
следующим образом: построим на поверхности
достаточно малый замкнутый контур, на
котором задано направление обхода.
Построим вектор нормали в точке
поверхности, лежащей внутри контура.
Если из конца вектора нормали обход
контура кажется происходящим против
часовой стрелки, то будем называть
сторону поверхности, обращенную к
вектору нормали положительной стороной.
Таким образом, будем рассматривать
ориентированную двухстороннюю
поверхность, а односторонние поверхности
лист Мебиуса, бутылку Клейна оставим в
покое. Потоком векторного поля ![]() через
ориентированную поверхность называется
поверхностный интеграл по площади
поверхности (1-го рода)
через
ориентированную поверхность называется
поверхностный интеграл по площади
поверхности (1-го рода) ![]() ,
где -
,
где - 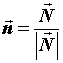 единичный вектор нормали, направленный
в положительную сторону. Выбор
положительной стороны обычно диктуется
физическими условиями задачи.
единичный вектор нормали, направленный
в положительную сторону. Выбор
положительной стороны обычно диктуется
физическими условиями задачи.
Гидродинамический смысл потока
Рассмотрим физический смысл потока векторного поля на примере гидродинамической задачи о вычислении количества жидкости, протекающей через поверхность S в единицу времени.
Каждой точке заполненного жидкостью пространства можно поставить в соответствие вектор скорости υ частиц потока текущей жидкости.
Разложим вектор υ скорости движения жидкости вблизи площадки на две составляющие, одна из которых направлена вдоль поверхности dS, а другая – перпендикулярно к ней. За протекание жидкости через площадку ответственна только нормальная составляющая скорости υn = υ · n, где n – единичный вектор нормали к поверхности dS.
За время dt через площадку пройдет жидкость, отстоящая от нее на расстоянии υn dt и заполняющая объем υn dt dS .
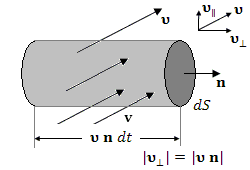
Объем жидкости, протекающей через бесконечно малую проницаемую площадку dS за время dt, равен (с точностью до знака)
dV = υ · n dt dS = υn dt dS.
В единицу времени через поверхность dS проходит dΦ = υn dS единиц объема жидкости. Эта величина называется потоком вектора υ через элемент поверхности dS .
Для нахождения потока Φ некоторого вектора через поверхность конечных размеров можно разбить эту поверхность на малые элементы и просуммировать потоки через все элементы. Результатом такого суммирования является интегральная сумма, которая переходит в соответствующий поверхностный интеграл при замене элементов конечных размеров бесконечно малыми элементами разбиения поверхности.
Таким образом, поток вектора A через поверхность S (например, количество жидкости, протекающей через S в единицу времени) равен поверхностному интегралу от проекции вектора на нормаль к поверхности:
![]() .
.
Дивергенция Векторного поля
Пусть
задано векторное поле ![]()
Определение 3.7.
Дивергенцией или расходимостью
векторного поля ![]() называется
скалярная функция, определяемая
равенством:
называется
скалярная функция, определяемая
равенством:

На этот раз векторное поле порождает скалярное поле div .
С учетом понятий дивергенции и потока векторного поля формулу Остроградскогоможно представить в форме:
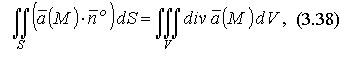
т. е. поток векторного поля через замкнутую поверхность S в направлении внешней нормали равен тройному интегралу от дивергенции векторного поля по области, ограниченной этой поверхностью.
На
основании формулы (3.38) можно записать: 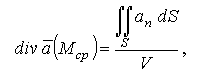 и,
переходя к пределу, стягивая V в
точку М (при
этом величина V → 0 ),
имеем:
и,
переходя к пределу, стягивая V в
точку М (при
этом величина V → 0 ),
имеем:

То есть div есть предел отношения потока поля через бесконечно малую замкнутую поверхность, окружающую точку М, к величине объёма, ограниченного этой поверхностью. Из этого следует, что дивергенция не зависит от выбора системы координат.
Если
поток  ,
то в область V втекает
большее количество жидкости (если
следовать ранее рассмотренному примеру
о течении несжимаемой жидкости), чем
вытекает из неё, т.е. внутри области V имеются
источники жидкости.
,
то в область V втекает
большее количество жидкости (если
следовать ранее рассмотренному примеру
о течении несжимаемой жидкости), чем
вытекает из неё, т.е. внутри области V имеются
источники жидкости.
Если П < 0, то внутри области V есть стоки. Но поток векторного поля характеризует интенсивность источников и стоков лишь суммарно, т.е. при П ≥ 0 внутри области V могут быть как источники, так и стоки.
Для характеристики точки можно использовать div .
Если div > 0, то данная точка есть источник, если div < 0 – то сток.
Заметим,
что div
можно
записать с помощью символического
вектора Гамильтона
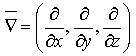 в
следующем виде:
в
следующем виде:
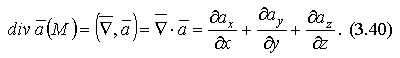
Отметим свойства дивергенции (справедливость которых рекомендуется показать самостоятельно):

где U – скалярная функция.
Пример 3.20.
Найти div ![]() ,
а также определить по формуле Остроградского
поток векторного поля
=
(x, y, z) через
замкнутую поверхность S.
Привести частные случаи.
,
а также определить по формуле Остроградского
поток векторного поля
=
(x, y, z) через
замкнутую поверхность S.
Привести частные случаи.
Решение
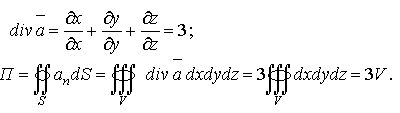
Цилиндр с высотой Н и радиусом основания R: П = 3πR2H. Конус с высотой Н и радиусом основания R: П = πR2H. Сфера радиуса R: П = 4R3.
Формула Гаусса – Остроградского.
Формула Гаусса – Остроградского является аналогом формулы Грина – Остроградского. Эта формула связывает поверхностный интеграл второго рода по замкнутой поверхности с тройным интегралом по пространственной области, ограниченной этой поверхностью.
Для вывода формулы Гаусса – Остроградского надо воспользоваться рассуждениями, подобными тем, которые использовались при нахождении формулы Грина – Остроградского.
Рассматривается сначала поверхность, ограниченная сверху и снизу некоторыми поверхностями, заданными известными уравнениями, а сбоку ограниченную цилиндрической поверхностью. Затем рассматривается вариант когда поверхность ограничена цилиндрической поверхностью с образующими, параллельными дум доугим координатным осям.
После этого полученные результаты обобщаются, приводя к формуле Гаусса – Остроградского:
![]()
Отметим, что эта формула применима для вычисления поверхностных интегралов по замкнутой поверхности.
На практике формулу Гаусса – Остроградского можно применять для вычисления объема тел, если известна поверхность, ограничивающая это тело.
Тиеют место формулы:
![]()
Пример. Найти формулу вычисления объема шара.
В поперечных сечениях шара (сечения параллельны плоскости XOY) получаются окружности.
Уравнение
шара имеет вид: ![]()
Найти объем шара можно по формуле:


Ротор (вихрь) векторного поля
![]()
или в символическом виде

Свойства ротора
![]()
![]()
![]()
Циркуляция векторного поля по замкнутому контуру. Теорема Стокса.
Проведем
в векторном поле замкнутую кривую и
примем для нее определенное направление
обхода. Затем разобьем ее на малые дуги.
Хорды, стягивающие эти элементы кривой,
имеют направления, совпадающие с
направлением обхода. Обозначим
их ![]() . В
произвольной точке i –того участка
кривой возьмем вектор поля
. В
произвольной точке i –того участка
кривой возьмем вектор поля ![]() и
составим сумму
и
составим сумму
![]() (2.37)
(2.37)
После этого устремим к нулю. Если при этом предел суммы (2.37) существует и не зависит от способа разбиения кривой и выбора точек определения векторов , то мы приходим к криволинейному интегралу
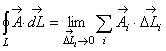 (2.38)
Определение. Криволинейный
интеграл (2.38) называется циркуляцией
векторного поля
(2.38)
Определение. Криволинейный
интеграл (2.38) называется циркуляцией
векторного поля ![]() по замкнутому контуру L.Если,
например,
- это силовое поле, то физический смысл
циркуляции состоит в том, что она выражает
работу поля по пути L.
Будем стягивать контур, по которому
вычисляется циркуляция, к точке. Это
позволит определить новую локальную
характеристику отличную от дивергенции.
Отличие заключается в частности в том,
что ее значение будет в общем случае
зависеть не только от точки, к которой
стягивается контур, но и от его ориентации
в пространстве. Поэтому можно предположить,
что интересующеенас предельное
значение циркуляции, которая сама по
себе есть скаляр, выражается через
скалярноепроизведение некоего
вектора (его предстоим нам найти) и
единичного вектора нормали к плоскости
контура, стягиваемого к точке.Возьмем
в поле
по замкнутому контуру L.Если,
например,
- это силовое поле, то физический смысл
циркуляции состоит в том, что она выражает
работу поля по пути L.
Будем стягивать контур, по которому
вычисляется циркуляция, к точке. Это
позволит определить новую локальную
характеристику отличную от дивергенции.
Отличие заключается в частности в том,
что ее значение будет в общем случае
зависеть не только от точки, к которой
стягивается контур, но и от его ориентации
в пространстве. Поэтому можно предположить,
что интересующеенас предельное
значение циркуляции, которая сама по
себе есть скаляр, выражается через
скалярноепроизведение некоего
вектора (его предстоим нам найти) и
единичного вектора нормали к плоскости
контура, стягиваемого к точке.Возьмем
в поле ![]() замкнутый
контур L,
натянем на него произвольную поверхность S и
определим на ней направление внешней
нормали. Построим на ее малом участке,
который в пределе можно считать плоским,
прямоугольник. Его стороны обозначим
замкнутый
контур L,
натянем на него произвольную поверхность S и
определим на ней направление внешней
нормали. Построим на ее малом участке,
который в пределе можно считать плоским,
прямоугольник. Его стороны обозначим ![]() и
и ![]() ,
причем
,
причем ![]() .
Площадь этого прямоугольника
.
Площадь этого прямоугольника
![]() (2.39)
(2.39)
, а вектор единичной нормали
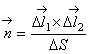 (2.40)
(2.40)
Вычислим
циркуляцию вектора ![]() вдоль контура
прямоугольника. С учетом последующего
перехода к пределу
вдоль контура
прямоугольника. С учетом последующего
перехода к пределу ![]() она
равна
она
равна
 (2.41)
(2.41)
,
где ![]() означает
бесконечно малую более высокого порядка,
чем
означает
бесконечно малую более высокого порядка,
чем ![]() .
.
Разделим
правую и левую части (2.41) на ![]() и
перейдем к пределу. Тогда с учетом того,
что в левой части стоит выражение для
циркуляции
вдоль
бесконечно малого контура, получим
и
перейдем к пределу. Тогда с учетом того,
что в левой части стоит выражение для
циркуляции
вдоль
бесконечно малого контура, получим
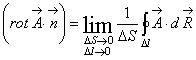 (2.42)
(2.42)
Проекция ![]() на
направление
на
направление ![]() равна
пределу отношения циркуляции
вектора
вдоль
замкнутого контура, проведенного в
плоскости, перпендикулярной
равна
пределу отношения циркуляции
вектора
вдоль
замкнутого контура, проведенного в
плоскости, перпендикулярной ![]() ,
к площади, ограниченной этим контуром,
при стягивании его к точке. Рассмотрим
теперь всю совокупность элементарных
площадок, на которые с помощью
прямоугольников, подобных только что
рассмотренному, можно разбить
поверхность S.
Применим к каждой из них соотношение
(2.41), просуммируем и перейдем к пределам,
как это было сделано при выводе (2.42).
Сумма правых частей
приведет нас к
потоку
,
к площади, ограниченной этим контуром,
при стягивании его к точке. Рассмотрим
теперь всю совокупность элементарных
площадок, на которые с помощью
прямоугольников, подобных только что
рассмотренному, можно разбить
поверхность S.
Применим к каждой из них соотношение
(2.41), просуммируем и перейдем к пределам,
как это было сделано при выводе (2.42).
Сумма правых частей
приведет нас к
потоку ![]() через
поверхность S.
Сумма
левых частей сведется к циркуляции
векторного поля
по
контуру L,
так как общие части границ соседних
элементарных площадок проходятся в
противоположном направлении и при
суммировании циркуляции их вклады
компенсируют друг друга. Из сказанного
следует
через
поверхность S.
Сумма
левых частей сведется к циркуляции
векторного поля
по
контуру L,
так как общие части границ соседних
элементарных площадок проходятся в
противоположном направлении и при
суммировании циркуляции их вклады
компенсируют друг друга. Из сказанного
следует
ТЕОРЕМА. Поток вихря через поверхность S,.натянутую на замкнутый контур L , равен циркуляции векторного поля по этому контуру, если компоненты поля вместе с их частными производными непрерывны на S и L.

Формула Грина
формула Грина касается криволинейных интегралов 2-го рода по замкнутому контуру.
Пусть ![]() -
кусочно-гладкая,
-
кусочно-гладкая, ![]() -
кусочно-гладкие
-
кусочно-гладкие
![]() -
непрерывны, за исключением площади
области 0. Тогда
-
непрерывны, за исключением площади
области 0. Тогда
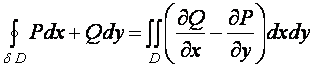

Область
называется простой, если ![]()
 D
D
a ![]() b
b
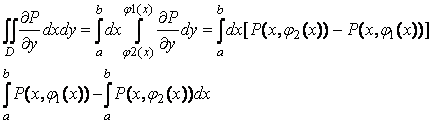
конечная сумма простых областей = D
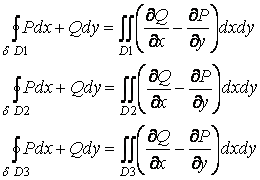



Следствие ![]()
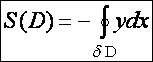
![]()
![]()
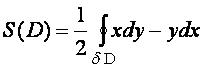
Дифференциа́льное
уравне́ние — уравнение,
связывающее значение некоторой
неизвестной функции в
некоторой точке и значение
её производных различных
порядков в той же точке. Дифференциальное
уравнение содержит в своей записи
неизвестную функцию, ее производные и
независимые переменные; однако не любое
уравнение, содержащее производные
неизвестной функции, является
дифференциальным уравнением. Например, ![]() не
является дифференциальным уравнением.
Стоит также отметить, что дифференциальное
уравнение может вообще не содержать
неизвестную функцию, некоторые её
производные и свободные переменные, но
обязано содержать хотя бы одну из
производных.
не
является дифференциальным уравнением.
Стоит также отметить, что дифференциальное
уравнение может вообще не содержать
неизвестную функцию, некоторые её
производные и свободные переменные, но
обязано содержать хотя бы одну из
производных.
Порядок, или степень дифференциального уравнения — наибольший порядок производных, входящих в него.
Решением (интегралом) дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,y(n)(x) до порядка nвключительно и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Вопрос об интегрировании дифференциального уравнения считается решенным, если нахождение неизвестной функции удается привести к квадратуре, независимо от того, выражается ли полученный интеграл в конечном виде или нет.
Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы.
Что называется дифферинциальным уравнением? Диферинциальное уравнение 1го порядка: с разделяющимися переменными, линейные ДУ, Уравнение Бернулли, однородные ДУ, уравнения в полных дифферинциалах. Дифференциа́льное уравне́ние — уравнение, связывающее значение некоторой неизвестной функции в некоторой точке и значение её производных различных порядков в той же точке.
Уравнение с разделяющимися переменными
![]()
![]()
![]()
![]() Общий
интеграл
Общий
интеграл
![]()
![]()
![]()
![]()
Линейное однородное уравнение первого порядка
![]()
![]()
Общее
решение: ![]()
![]() .
.
Решение задачи Коши, y(x0) = y0:
![]()
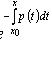
Линейное неоднородное уравнение первого порядка
![]()
![]()
Общее решение:
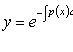
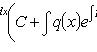
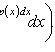
Решение задачи Коши, y(x0) = y0:
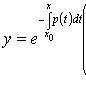
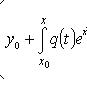
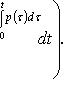
Линейное однородное уравнение второго порядка с постоянными коэффициентами
![]()
![]()
Характеристическое
уравнение
![]()
![]() Характеристические
числа
Характеристические
числа
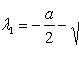
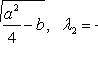
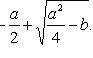
![]() Данное
уравнение является уравнением Бернулли.
Для его решения сделаем замену
Данное
уравнение является уравнением Бернулли.
Для его решения сделаем замену ![]() :
:
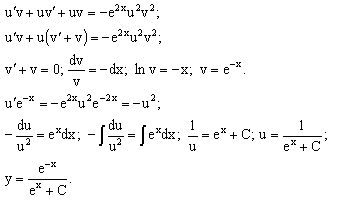 Учитывая
y(0)=1, получим:
Учитывая
y(0)=1, получим: ![]() Следовательно,
Следовательно, ![]() Ответ:
Ответ:
Теорема о существовании и единственности диферинциалного уравнения первого порядка
Теорема:
Пусть![]() в
уравнении
в
уравнении ![]() (1)
определена в области
(1)
определена в области ![]() ,
непрерывна в ней, и имеет непрерывную
частную производную
,
непрерывна в ней, и имеет непрерывную
частную производную ![]() в
этой области. Тогда
в
этой области. Тогда ![]() ,
что в
,
что в ![]()
![]() решение
уравнению (1), удовлетворяющее условию
решение
уравнению (1), удовлетворяющее условию ![]() (2)
и оно единственно.
(2)
и оно единственно.
Доказательство:
Лемма: Задача Коши (1)-(2) равносильна решению интегрального уравнения
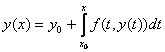 (3).
Т.е. если y(x) удовлетворяет уравнению
(1) и условию (2), то оно является решением
(3) и обратно: если y(x) в некотором интервале,
содержащем точку
(3).
Т.е. если y(x) удовлетворяет уравнению
(1) и условию (2), то оно является решением
(3) и обратно: если y(x) в некотором интервале,
содержащем точку ![]() удовлетворяет
(3) и является непрерывной функцией, то
она является решением задачи Коши.
удовлетворяет
(3) и является непрерывной функцией, то
она является решением задачи Коши.
Доказательство Леммы:
1) ![]() Пусть
y(x) удовлетворяет (1) и (2). Это значит,
что
Пусть
y(x) удовлетворяет (1) и (2). Это значит,
что ![]() .
Проинтегрируем:
.
Проинтегрируем:


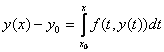
2) ![]() Пусть
y(x) удовлетворяет (3) и является непрерывной
функцией, тогда подынтегральная
функция
Пусть
y(x) удовлетворяет (3) и является непрерывной
функцией, тогда подынтегральная
функция ![]() -
непрерывная, как суперпозиция непрерывных
функций. Тогда интеграл с переменным
верхнем приделом – функция диф-ая.
Подставим y(x) в (3). Мы имеем право диф-ть
(3) по х.
-
непрерывная, как суперпозиция непрерывных
функций. Тогда интеграл с переменным
верхнем приделом – функция диф-ая.
Подставим y(x) в (3). Мы имеем право диф-ть
(3) по х.
![]() -
удовлетворяет (1). Кроме того, подставив
в (3) вместо x,
мы
получим, что у удовлетворяет и нач.
условию (2).
-
удовлетворяет (1). Кроме того, подставив
в (3) вместо x,
мы
получим, что у удовлетворяет и нач.
условию (2).
дифференциальные уравнения высших порядков допускающие понижение порядка

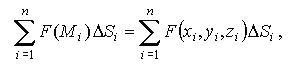
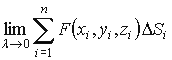
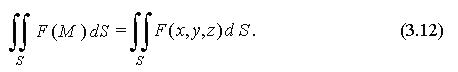
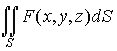
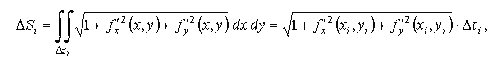
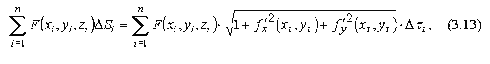
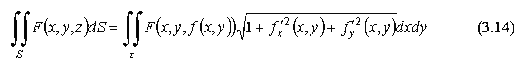
 усть
задана дифференцируемая функция
скалярного поля
.
усть
задана дифференцируемая функция
скалярного поля
.