1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.

Рассмотрим уравнения вида

                                                             .                                                (2)

С помощью замены  , где u  - новая неизвестная функция,  уравнение (2) приводится к уравнению (n-k) -го порядка:

 .

2. Уравнения, не содержащие явно независимой переменной.

Рассмотрим уравнения вида

                                                                .                                                                     (3)

С помощью замены   (где p=p(y) - новая искомая функция независимая переменная) порядок уравнения (3) понижается на единицу, так как

,

,

..........................................................

.

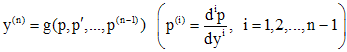Данная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:

.

При осуществлении такой замены возможна потеря решения y=const. Непосредственной подстановкой необходимо проверить наличие у уравнения (3) решений такого вида.

3. Уравнения, однородные относительно .

Рассмотрим уравнения вида

                                                        ,                                                                          (4)

где F является однородной с показателем m относительно  , т.е.

.

С помощью замены  , где u - новая неизвестная функция, порядок уравнения (4) понижается на единицу. Имеем

,

.................................

.

Данная подстановка дает дифференциальное уравнение (n-1) - го порядка относительно новой неизвестной функции u:

4. Обобщенно - однородные уравнения.

 Рассмотрим уравнения вида

                                                                   .                                                               (5)

Уравнение (5) называется обобщенно - однородным, если существуют числа k и m такие, что

.

С помощью замены (при x<0 полагаем  )

,

где t - новая независимая переменная, u - новая искомая функция, уравнение (5) приводит к уравнению, не содержащему независимой переменной t и, следовательно, допускающему понижение порядка на единицу (см. п. 2).

Производные при данной замене преобразуются по формулам

......................................................................

.

Подстановка последних равенств в (5) дает уравнение вида

,

которое явно не содержит независимую переменную t.

5. Уравнение в точных производных.

 Рассмотрим уравнения вида

                                                                   ,                                                               (1)

левые части которых являются точными производными от некоторой функции  , т.е.

.

Такие уравнения называются уравнениями в точных производных. Из последнего равенства следует, что соотношение

является первым интегралом уравнения (1) - уравнением (n-1) - го порядка относительно искомой функции. Таким образом, уравнение в точных производных допускают понижение порядка на единицу.

 Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами 

     Характеристическое уравнение 

 - корни характеристического уравнения.

     Общее решение 

     1. Все корни характеристического уравнения различные, тогда

     Если среди корней есть пары комплексно-сопряженных корней, например  , решение можно записать в виде

     2. Среди корней характеристического уравнения есть кратные, например,   имеет кратность k (остальные - простые), тогда

     Если среди корней есть пары сопряженных корней кратности k, например  , решение можно записать в виде

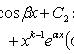
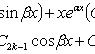
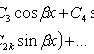
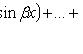
Линейный дифференциальный оператор и его свойства. Множество функций, имеющих на интервале (a, b) не менее n производных, образует линейное пространство. Рассмотрим оператор L_n(y), который отображает функцию y(x), имеющую   производных, в функцию, имеющую k - n производных:

С помощью оператора неоднородное уравнение можно записать так:

Ln(y) = f(x);

Правило вычисления фундаментальной системы решений линейных ДУ второго порядка с постоянными коэфицентами.

     Линейное неоднородное уравнение с постоянными коэффициентами 

     Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и некоторого частного решения  неоднородного уравнения.

Вид частного решения y* неоднородного уравнения в некоторых конкретных случаях 

(  - заданные многочлены степени m, l;   - искомые многочлены степени не выше m, k)

     1.  :

     a) число 0 не является корнем характеристического уравнения, тогда

     б) число 0 - корень кратности s характеристического уравнения:

     2.  :

     a) число a не является корнем характеристического уравнения, тогда

     б) число a - корень кратности s характеристического уравнения:

     3.  :

     a) числа   не являются корнями характеристического уравнения, тогда

     б) числа   - корни кратности s:

     4.  :

     a) числа   не являются корнями характеристического уравнения, тогда

     б) числа   - корни кратности s:

Линейное неоднородное дифференциальное уравнение n-го порядка Структура общего решения

Для линейного неоднородного дифференциального уравнения n-го порядка

y⁽ⁿ⁾ + a₁(x) y^(n-1) + ... + a_n-1 (x) y' + a_n(x) y = f(x), 

где y = y(x) — неизвестная функция, a₁(x), a₂(x), ..., a_n-1(x), a_n(x), f(x) — известные, непрерывные, справедливо:  1) если y₁(x) и y₂(x) — два решения неоднородного уравнения, то функция y(x) = y₁(x) - y₂(x) — решение соответствующего  однородного уравнения; 2) если y₁(x) решение неоднородного уравнения, а  y₂(x) — решение соответствующего однородного уравнения, то функция y(x) = y₁(x) + y₂(x) — решение неоднородного уравнения; 3) если  y₁(x), y₂(x), ...,  y_n(x) — n линейно независимых решений однородного уравнения, а y_ч(x) — произвольное решение неоднородного уравнения,  то для любых начальных значений  x₀,  y₀,   y_0,1, ..., y_0,n-1  существуют такие значения  c*₁, c*_n, ..., c*_n, что решение  y*(x)=c*₁ y₁(x) + c*₂ y₂(x) + ... + c*_n y_n (x) + y_ч(x) удовлетворяет при x = x₀ начальным условиям y*(x₀)=y₀, (y*)'(x₀)=y_0,1 , ...,(y*)^(n-1)(x₀)=y_0,n-1.

Выражение  y(x)= c₁ y₁(x) +  c₂ y₂(x) + ... + c_n y_n(x)   + y_ч(x)  называется общим решением линейного неоднородного дифференциального уравнения n-го порядка.

Для отыскания частных решений неоднородных дифференциальных уравнений с постоянными коэффициентами с правыми частями вида:  P_k(x)exp(ax)cos(bx) + Q_m(x)exp(ax)sin(bx),  где P_k(x), Q_m(x) — многочлены степени k и m соответственно, существует простой алгоритм построения частного решения, называемый методом подбора.

Метод подбора, или метод неопределенных коэффициентов, состоит в следующем.  Искомое решение уравнения записывается в виде: (P_r(x)exp(ax)cos(bx) + Q_r(x)exp(ax)sin(bx))x^s,  где P_r(x), Q_r(x) — многочлены степени r = max(k, m) с неизвестными коэффициентами p_r , p_r-1, ..., p₁, p₀, q_r, q_r-1, ..., q₁, q₀.  Сомножитель x^s называют резонансным сомножителем. Резонанс имеет место в случаях, когда среди корней характеристического уравнения есть корень l =a ± ib  кратности s.

Правило вычисления частного решения линейного неоднородного дифферинциального уравнения второго порядка с правой частью специального вида

 Метод подбора частного решения неоднородного уравнения с правой частью специального вида. Методом Лагранжа может быть решено любое неоднородное уравнение с постоянными коэффициентами. Однако если свободный член в уравнении имеет вид

.

где P_m1(x) и Q_m2(x) - многочлены степеней, соответственно, m₁ и m₂, можно сразу указать вид частного решения в форме с неопределёнными коэффициентами. Общее правило таково: составим из коэффициентов при x в экспоненте и тригонометрических функциях число   и пусть r - кратность числа s₀ как корня характеристического уравнения, m = max(m₁, m₂). Тогда частное решение надо искать в виде  , где R_m(x) и S_m(x) - многочлены степени m с неопределёнными коэффициентами. Дифференцируя функцию y_чн n раз, подставив эти производные в уравнение и приравнивая коэффициенты при одинаковых степенях x и одинаковых тригонометрических функциях (sin x или cos x), получим систему из 2(m + 1)уравнений относительно 2(m + 1) неопределённых коэффициентов многочленов R_m(x) и S_m(x). Решив эту систему, определим коэффициенты функции y_чн(x).  Технику работы с этим правилом будем осваивать, начиная с простейших случаев, при этом будем формулировать частные правила, вытекающие из общего.  I. Если f(x) = P_m(x) (т.е. f(x) - многочлен степени m), то частное решение ищется в виде y_чн(x)= R_m(x), если число 0 не является корнем характеристического уравнения, и в виде y_чн(x)= x^rR_m(x), если число 0 - корень характеристического уравнения кратности r. R_m(x) - многочлен степени m с неопределёнными коэффициентами.  Это правило следует из общего, если записать f(x) = P_m(x) в виде f(x) = e^0 x [P_m(x) cos 0x + 0 sin 0x]. В этом случае s₀ = 0 + 0i, m₁ = m, m₂ = 0, max(m₁, m₂) = m, поэтому  y_чн(x)= x^r e^0 x [R_m(x) cos 0x + S_m(x) sin 0x] = x^r R_m(x) . 

Метод вариации постоянных (метод Логранжа)

Метод вариации произвольных постоянных. Если коэффициенты уравнения постоянны, то, как следует из результатов предыдущего раздела, можно найти фундаментальную систему решений однородного уравнения, и, следовательно, применить метод вариации произвольных постоянных для решения неоднородного уравнения. Пример: найти общее решение уравнения  . По теореме 14.5.9. о структуре общего решения неоднородного уравнения общее решение этого уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения. Характеристическое уравнение соответствующего однородного уравнения: k² + 4 k - 5 = 0. Его корни    . Фундаментальная система решений y₁(x) = e ^-5x, y₂(x) = e ^x, y_оо(x) = C₁ e ^-5x + C₂ e^x. Ищем решение исходного уравнения в виде y(x) = C₁(x) e ^-5x + C₂(x)e^x. В соответствии с методом вариации система для нахождения     будет   Решаем эту систему:  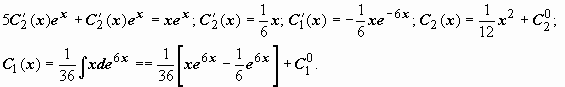    Общее решение:  (константы в окончательном ответе переобозначены).

Что называется частичной суммой ряда? Суммой ряда? Примеры числовых рядов: гармонический ряд, геометрическая прогрессия, ряд Дирихле. При каком условии сходится геометрическая прогрессия? Основные задачи теории числовых рядов.

Пусть   — последовательность чисел. Число  называется n-ой частичной суммой ряда  .

Сумма (числового) ряда — это предел частичных сумм Sn, если он существует и конечен. Таким образом, если существует число  , то в этом случае пишут  .

 гармонический ряд представляет собой сумму, составленную из бесконечного количества членов, обратных последовательным числам натурального ряда^[1]:

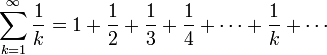
Отдельные члены ряда стремятся к нулю, но его сумма расходится. n-ной частичной суммой s_n гармонического ряда называется n-ное гармоническое число:

Геометри́ческая прогре́ссия — последовательность чисел   (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число   (знаменатель прогрессии), где  ,  :  ^[1].

Любой член геометрической прогрессии может быть вычислен по формуле:

Если b₁ > 0 и q > 1, прогрессия является возрастающей последовательностью, если 0 < q < 1, — убывающей последовательностью, а при q < 0 — знакопеременной.

Своё название прогрессия получила по своему характеристическому свойству:

Рядом Дирихле называется ряд вида

где s и a_n — комплексные числа, n = 1, 2, 3, … .

Абсциссой сходимости ряда Дирихле называется такое число σ_c, что при   он сходится; абсциссой абсолютной сходимости называется такое число σ_a, что при   ряд сходится абсолютно. Для любого ряда Дирихле справедливо соотношение   (если σ_c и σ_a конечны).