18.Двоїста задача (дз). Правила побудови дз. Симетричні й несиметричні дз.

Для побудови ДЗ необхідно звести пряму задачу до стандартного виду. Вважають, що ЗЛП подана у станд. вигляді, якщо для відшукання маx. Знач-я цільової функції всі нерівності її системи обмеж-ь приведені до виду «≤», а для задачі на відшукання мін. значення - до виду «≥». Якщо пряма ЗЛП подана в станд. вигляді, то ДЗ утворюється за такими правилами: 1.Кожному обмеж-ю прямої задачі відповід двоїста змінна. Кіл-ь змінних ДЗ=кіл-ті обмеж-ь прямої задачі. 2.Кожній змінній прямої задачі відповідає обмеж-я ДЗ, причому кіл-ть обмежень ДЗ=кіл-ті змінних прямої задачі. 3.Якщо цільова функція прямої задачі задається на пошук max значення, то цільова функція ДЗ - на визначення min, і навпаки. 4.Коефіцієнтами при змінних у цільовій функції ДЗ є праві частини обмежень прямої задачі. 5.Праві частини системи обмежень ДЗ є коефіцієнтами при змінних у цільовій функції прямої задачі. 6. Матриця, що склад-я з коефіцієнтів при змінних у системі обмежень прямої задачі, є транспонованою матрицею до матриці із коефіцієнтів у системі обмежень ДЗ. Пряма і ДЗ утвор-ь двоїсту пару або пару спряжених задач. Всі двоїсті пари поділ-я на симетричні та несиметричні. У симетричних задачах обмеж-я прямої та двоїстої задач є лише нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень. У неси метр-их задачах деякі обмеж-я прямої задачі можуть бути рівняннями, а ДЗ - лише нерівностями. У цьому разі відповідні рівнянням змінні ДЗ можуть набувати будь-яких значень, не обмежених знаком.

32.Сідлова точка та необхідні і достатні умови її існування. Теорема Куна-Таккера

Сідлова точка - 1н із типів стаціонарних точок ф-ії багатьох змінних,в якому 1ші похідні ф-ії дорівнюють 0, але матриця 2их похідних не є додатньо визначеною.

Необхідні умови сідлової точки:

для тих індексів j, де .

для тих індексів j, де .

, - довільного знака.

для тих індексів і, де ,

для тих індексів і, де ,

для тих інд-в і,де має довіл-й знак.

Теорема Куна-Таккера дає змогу встановити типи задач,для яких на множині допустимих розв'язків існує лише 1н глобал-й екстремум зумовл-о типу.Вона тісно пов'язана з необхід-и і достат-и умовами існув-я сідлової точки.Розглянемо задачу нелін-го програмув-я, яку,не зменшуючи загальності,подамо у вигляді: maxF=ƒ(X), (1) qi(X)≤bi (i=1,m), (2) xj ≥0 (j=1,n) (3)

У теоремі вектор X* є опти­мальним розв'язком задачі (1)-(3) тоді і тільки тоді,коли існує такий вектор ٨*, що при X* ≥ 0,٨*≥ 0 для всіх Х≥0, ٨≥0 точка (Х*,٨*) є сідловою точкою функції Лагранжа L(X,٨)= ƒ(X)+ λi (bi - qi(X)),і ф-ія мети f(X) для всіх Х≥0 угнута, а ф-ії qi(X (i = 1,m) -опуклі.

33.Квадратична функція та її властивості

Квадрат-а ф-ія n змінних називається квадратичною формою(КФ) і може бути подана у вигляді:

, де , , ,

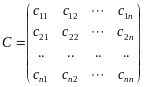причому матриця С завжди симетрична,тобто Cij=Cji для всіх i,j=1,n.

КФ Z(X) назив-ся від’ємно означеною,якщо для всіх Х, крім Х=0,значення Z(X) < 0 (якщо Z(X)≤0,то маємо від’ємно напівозначену КФ),у протилеж-у разі Z(X) є додатно означ-ю (якщо Z(X)≥0,то маємо додатно напівознач-у КФ).КФ Z(X) назив-ся неознач-ю, якщо вона додатня для 1х значень Х і від’ємна для інших.

Вид КФ можна визначити, використ-чи - вектор характерист-х коренів (власних значень) матриці С.Для того,щоб довільна КФ була додатно (від’ємно) означеною,необхідно і достатньо,щоб усі компоненти вектора характерист-х коренів були додатними (від’ємними) значеннями.Якщо хоча б 1н із характерис-х коренів дорівнює 0,то КФ є напівдодатною (напіввід’єм). Якщо корені мають різні знаки,то КФ є неозначеною.