Iнтегральний закон розподiлу

Інтегральним законом розподілу ВВ (ВСП) називають функцію ймовірності F(x), значення якої для кожного значення х , вибраного на осі абсцис, визначається тим, що результат спостереження Х в і-тому досліді приймає значення менші за х, що з точки зору теорії ймовірності записується так:

F(x) = P(Х x ) = P( - < X ≤ x). (3.21)

Ця функція розподілу F(x) існує для всіх ВВ (ВСП), як дискрет­них так i безперервних і є універсальною характеристикою ВВ (ВСП).

Графік функції розподілу F(x) у загальному випадку є графіком неспадаючої функції, значення якої починається від 0 на - та доходить до 1 на + і має S -подібну форму (рис.3.3).

Рис.3.3. Графік функції розподілу F(x) інтегрального закону.

Для випадку, коли ВВ Х=Q, тобто, коли результати вимірювань розміщені із правого та лівого боків від Q, то центр перегину S-образної функції розподiлу вiдповiдає ймовірності на рівні 0,5. В цьому випадкурозподіл результатів відносно істинного значення шуканої величини є симетричним.

Таким чином, інтегральна функція ймовірності F(x) дає уявлення про розміщення кожного окремого результату вимірювання Хі відносно істинного

значення вимірюваної величини.

Практично функція F(x) використовується для розрахунку ймовірності того, що

ВВ (ВСП) Х прийме значення, яке розташоване в деяких межах, яке розташоване

від "а" (із ліва) до "в" (із права) і дорівнює:

P("а" <= X < "в") = F("а") - F( "в"). (3.22)

Така ймовірність розташування випадкової величини на заданій ділянці дорівнює приросту функції розподiлу F(x) на цiй ділянці:

Диференцiйний закон розподiлу

Для більш наочного опису результатів вимірювання та випадкових похибок використовують, для безперервних випадкових величин, похідну від функції інтегрального розподілу F(x).

Якщо є безперервна (3.22) випадкова величина Х із функцією розподілу F(x), то можемо вирахувати ймовірність Р попадання цієї ВВ Х на відрізку від х до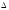 х+х:

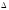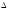P( x < X < x + x) = F ( x + x) - F(x),

тобто, імовірність дорівнює приросту функції розподілу F(x) на цьому відрізку.

Тепер розглянемо відношення цієї ймовірності до довжини відрізку, тобто, розглянемо середню ймовірність, яка приходиться на одиницю довжини цього відрізку та будемо наближати 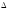x до 0. У крайній межі дістанемо похідну F' від функції інтегрального розподiлу:

lim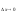 {[ F(x+x) - F(x)] / x} = F'(x) = P(x). (3.23)

Введене позначення функції P(x) – похідної від функції розподілу F(x) характеризує густину, з якою розподіляється значення випадкової величини Х в даній точці.

Функція P(x) називається густиною розподілу, або по іншому: "густиною ймовірності" безперервної випадкової величини Х, або диференціальною функцією розподілу, або диференціальним законом розподілу.

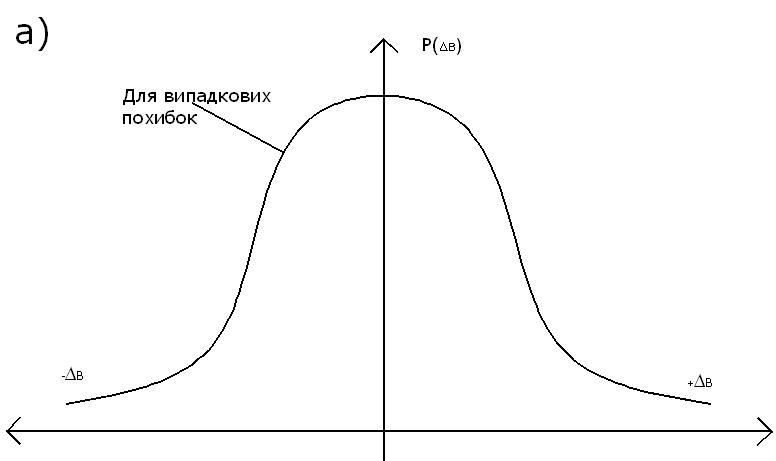
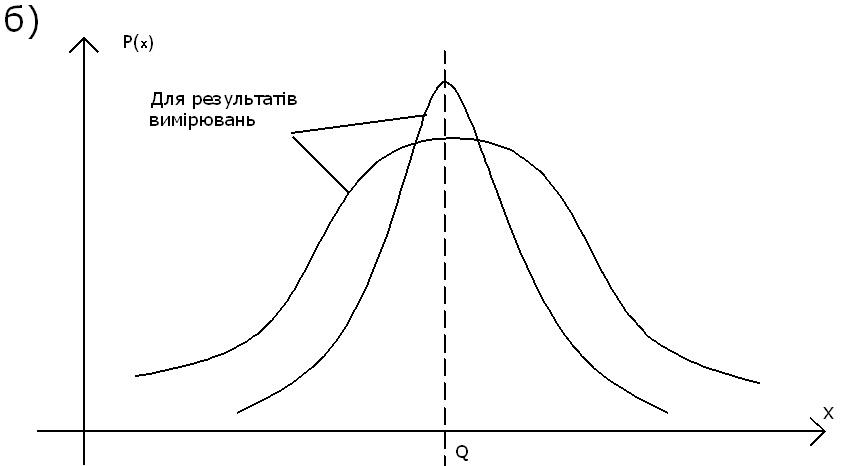
Рис.3.4. Крива розподілу Р(х) для ВСП - а) та РВ - б).

Густина розподілу Р(х), по аналогії з функцiєю розподiлу F(x), є ще

одною із форм закону розподiлу. У протилежність функції розподілу F(x) ця форма Р(x) не є універсальною, так як існує тільки для безперервних випадкових величин.

Графік, який відтворює густину розподілу Р(х) випадкової величини,

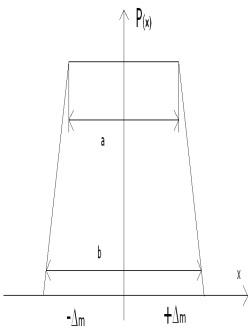
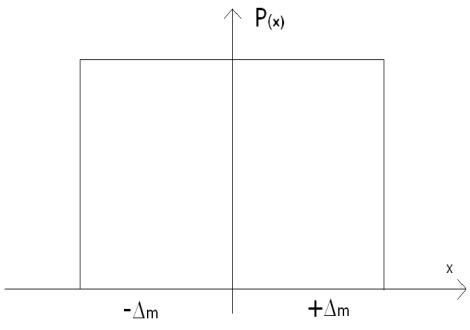
називається кривою розподілу, яка може бути як для випадкової складової похибки ВСП (рис. 3.4,а), так і для результатів вимірювання РВ (рис. 3.4,б). Криві розподілу мають різний вигляд (основні показані на рис. 3.5: трикутний, трапецієвидний, рівномірний і інші), який залежить від кількості впливаючих на подію ( щоб вона відбулася чи ні) факторів та вiд значення цих факторів.

а) б) в)

Рис. 3.5. Криві розподілу: трикутного - а), трапецієвидного - б) та

рівномірного – в) законів.

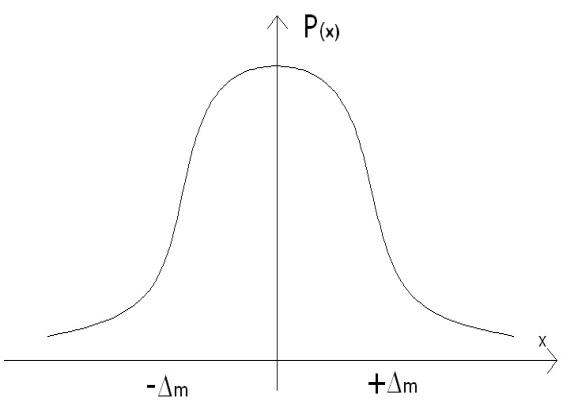
У більшості криві розподiлу мають форму, яка близька до дзвоноподiбної

(рис. 3.6) і відповідають нормальному закону розподілу.

а) б)

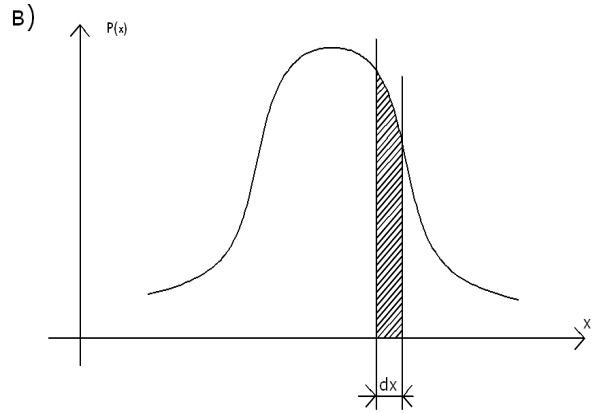
Рис. 3.6. Крива розподілу нормального закону (а) та елемент ймовірності (б).

Якщо розглянути безперервну випадкову величину Х із густиною розподілення Р(х) та елементарний відрізок dx, який прилягає до точки х, то ймовірність попадання випадкової величини Х на цю елементарну ділянку, з точністю до безмежних малих вищого порядку, дорівнює Р(x)dx i цю величину називають елементом імовірності. Геометрично - це площина елементарного прямокутника, який опирається на відрізок dx (рис. 3.6,б).

Використовування елементів імовірності дає можливість сказати про те, які інтервали значень випадкових похибок більш чи менш імовірні. Наприклад, при дзвоноподібний кривій розподілу Р(x) для випадкових похибок Δв більш ймовірні малі значення похибок, якi лежать навколо випадкової похибки із значенням Δв = 0. Можемо виразити ймовірність попадання випадкової величини Х на відрізок вiд "а" до "в" через густину розподілу. Очевидно, що вона буде дорівнювати сумі елементів імовірності на всьому відрізку, тобто, інтегралу: P("а" <X < "в") = 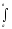Р(x) dx. (3.24)

Геометрична ймовірність попадання величини Х дорівнює площині кривої розподілу, яка опирається на цей відрізок.

Ми можемо вирішити й обернену задачу - виразити функцію розподілу F(x) через густину розподілу Р(x) . Так як по визначенню F(x) = P(X<x) = P(- < X < x), то використовуючи інтегральну формулу визначення густини розподілу, отримуємо: F(x) = 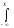Р(x)dx.

Геометрично ймовірність F(x) є, не що інше, як площина під кривою розподілу Р(x), яка лежить лівіше тачки х.

Розмірності основних характеристик випадкової величини: 1. Функція інтегрального розподілу F(x), як усяка ймовірність є величиною без розміру. 2. Розмірність густини розподілу P(x) - є обернена розмірності випадкової величини.