12 Теория потребительского выбора: ординалистская концепция. Кривые безразличия и бюджетное ограничение. Условия равновесия потребителя.

Ординалистская (порядковая) полезность — субъективная полезность (или удовлетворение, которое потребитель извлекает из потребляемого им блага), измеренная по порядковой шкале. В концепции ординаитской полезности утверждается, что количество полезности, полученной от потребляемого блага, не может быть измерено численно, как это подразумевается критериями кардиналистской теории. Вместо этого ординалисты предполагают упорядочение потребителем своих предпочтений в отношении благ.

Для моделирования потребительского выбора используются кривые безразличия и бюджетное ограничение (линия потребительских возможностей).

Кривые безразличия. Они позволяют описать поведение потребителя с помощью предпочтения или ранжирования благ. Впервые в экономический анализ они были введены итальянским экономистом В. Парето в начале 20-х годов XX века. Предпочтения потребителя касаются всех благ, однако для упрощения рассмотрим лишь два блага — X и Y.

Кривая безразличия — это множество точек, каждая из которых представляет такой набор из двух товаров, что потребителю безразлично, какой из этих наборов выбрать, поскольку их полезность одинакова. Кривую безразличия называют также равнополезным контуром.

Так, потребителю безразлично, какой набор выбрать:

6 батонов хлеба и 2 пакета молока,

4 батона хлеба и 4 пакета молока,

1 батон хлеба и 6 пакетов молока и т.п.

Данные наборы товаров имеют одинаковую полезность (равноценны), так что если соединить все точки, обозначающие наборы в пространстве двух товаров X (хлеб) и Y (молоко), то получим линии равных полезностей (кривые безразличия U1, U2, U3). Кривые безразличия подобны горизонталям (изогипсам) на парте местности, соединяющим точки с одинаковой высотой над уровнем моря.

Бюджетное ограничение — это геометрическое место точек, представляющих доступные потребителю комбинации товаров при неизменных ценах на них и фиксированном доходе. Кривые безразличия позволяют выявить потребительские предпочтения и возможность замены одного блага другим, но они не показывают, какой именно набор товаров потребитель считает для себя наиболее выгодным. Естественно, потребитель стремится приобрести товарный набор, расположенный на наиболее удаленной от начала координат кривой безразличия, но он ограничен в средствах. Не всякий товарный набор ему доступен. Для изображения множества доступных потребителю товарных наборов используется бюджетная линия (линия цен, расходов).

Пусть I — месячный доход потребителя. Он расходует его на приобретение двух товаров — X и Y. Px, Py — цены товаров X и Y. Бюджетное ограничение будет иметь вид: I = PxX+PyY

Бюджетная линия, или линия потребительских возможностей, — это линия, показывающая альтернативные сочетания благ, которые могут быть приобретены при данном уровне дохода и данных ценах.

Смысл бюджетного ограничения состоит в том, что доход потребителя равен сумме расходов на покупку товаров X и Y.

Преобразуем предыдущее равенство и получим уравнение бюджетной линии (линии цен):

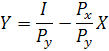
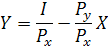
Если потребитель весь доход I израсходует на покупку товара X, то он сможет приобрести 1/Px. Если весь доход пойдет на приобретение товара Y, то потребитель купит 1/Py.

Стоимость всех товарных наборов, соответствующих точкам на бюджетной линии, равна доходу I руб. и поэтому они доступны потребителю. Все наборы, расположенные выше и правее бюджетной линии, стоят дороже и поэтому недоступны для потребителя. Таким образом, бюджетная линия ограничивает сверху множество доступных для потребителя наборов.

Y

I/Py

I/Px X

Равновесие потребителя — совокупность приобретаемых товаров и услуг, при которой полезность для потребителя максимизируется и одновременно соблюдается его бюджетное ограничение.