
- •1.1.Що є предметом теорії імовірності?
- •1.2.Дати означення підмножини скінченної (нескінченної), зліченої і незліченої. Навести приклад.
- •1.3.Суми, різниці та добутку множин. Навести приклади.
- •1.4.Дати означення сполучення та розміщення із n елементів по k, переставлення із n елементів. Записати позначення. Навести приклади
- •1.5. Записати формулу, що пов’язує число переставлень, сполучень та розміщень. Сформулювати правила суми та добутку, що вик при розв’язуванні комбінаторних задач. Навести приклади.
- •1.7. Дати означення сумісних, несумісних та попарно несумісних подій. Навести приклади.
- •1.8. Дати означення суми (об’єднання), різниці та добутку (перетину) подій, протилежної події, повної групи подій. Навести приклади.
- •1.9. Як випадкова подія виражається через елементарні наслідки випадкового експерименту? Які елементарні наслідки називаються такими, що сприяють появі даної події? Навести приклади.
- •1.10. Дати означення поняття імовірності випадкової події. Сформулювати класичне визначення імовірності події і записати відповідну формулу. Навести приклади.
- •1.11.(Геометричне визначення).
- •1.12. Дати означення частоти та відносної частоти події.
- •1.13. Сформулювати теореми: а) про імовірність суми двох подій; б) про імовірність суми двох несумісних подій; в) про імовірність суми декількох попарно несумісних подій. Навести приклади.
- •1.14. Дати означення незалежності і залежності двох подій, умовної імовірності події, попарної незалежності декількох подій, незалежності у сукупності декількох подій. Навести приклади.
- •1.15. Записати формулу для обчислення імовірності хочаб однієї з декількох подій, незалежних у сукуупності.Пояснити букви, навести приклади.
- •1.16. Записати формули: а) повної імовірності; б) Байеса. Пояснити зміст позначень. Навести приклади.
- •1.17. Навести умови схеми випробувань Бернулі. Записати формулу Бернулі.Навести приклади застосування.
- •1.18. Граничні теореми у схемі випробувань Бернулі. А)Пуассона. Б) Локальну та інтегральну Лапласа.
- •1.19.Записати формули для обчислення в схемі бернулі: а)імовірності відхилення частоти від імовірності б)найбільш імовірного числа появи подій
- •2.1. Дати означення випадкової величини (в.В.), дискретної (д.В.В.) та неперервної випадкої величини (н.В.В.). Навести приклади.
- •2.2. Дати означення закону та багатокутника розподілу ймовірностей д.В.В. Навести приклади.
- •2.3. Дати означення а) інтегральної; б) диференціальної функції розподілу н.В.В. Вказати їх основні властивості. Навести приклади.
- •2.5. Пояснити, що характеризують: а) математичне сподівання; б) дисперсія та середнє квадратичне відхилення; в) асиметрія; г) ексцес; д) мода; е) медіана.
- •2.6. Довести основні властивості математичного сподівання і дисперсії.
- •2.8.Записати основні закони розподілу н.В.В.: а) рівномірний; б) нормальний; в) показниковий. Пояснити зміст букв. Навести приклади н.В.В., розподілених за цими законами.
- •2.9.Що в теорії ймовірностей розуміють під терміном «Закон великих чисел»? Записати нерівність а. Чебишова. Пояснити зміст букв.
- •2.10.Сформулювати основні теореми закону великих чисел: а) Бернуллі; б) Чебишова; в) Центральну граничну теорему. Пояснити зміст букв.
- •2.12.Дати означення системі випадкових величин. Навести приклади. Дати означення закону розподілу дискретної двовимірної випадкової величини. Навести приклади.
- •2.13.Дати означення ф-ціїї розподілу двв. Основні властивості ф-ції розподілу, її геометричний зміст.
- •2.14.Дати означеня щільностей ймовірностей двв. Основні властивості, імовірнісний зміст.
- •2.15.Записати ф-ли для обчислення ймовірностей попадання випадкової точки в довільну двомірну область d; в прямокутник.
- •2.16. Означення залежності (незалежності) випадкових величин, що входять в с-му вв. Теореми про необхідну та достатню умови незалежності.
- •2.20. Навести основні властивості кореляційного моменту μxy та коефіцієнту кореляції rxy
- •2.21. Дати означення корельованості (некорельованості) двох в.В. Пояснити різнцю і зв’язок між корельованістю (некорельованістю) і залежністю двох в.В.
- •2.22. Вивести рівняння лінійної середньоквадратичної регресії y на х(х на y). Пояснити зміст позначень.Дати означення коефіцієнту регресії , залишкової дисперсії та пояснити, що вони характеризують.
- •2.23. Сформулювати теорему про корельованість складових нормально розподіленої двовимірної в.В.
- •2.26. Вказати вв що мають розподіл: Персона х2, Стьюдента, Фішера
- •3.1. Предмет мс є розробка методів, збору і обробки інформації, аналізу результатів обробки з метою одержання науково-обгрунтованих висновків і вироблення практичних рекомендацій.
- •3.2.Озн генеральної та вибіркової сукупності, об’єму вибірки, повторної і без повторної, репрезентативної вибірки
- •3.3.Озн статистичної (емпіричної) ф-ї розподілу, різниця між емпіричною і теоретичною ф-єю. Побудова графіків
- •3.4. Кумулятивної частоти та частостей.
- •3.5.Означення полігону, гістограми, кумулятивної частоти та частостей.
- •3.6.Означення статистичної оцінки параметра розподілу ген сукупності, незаміщеної еф обгр оцінки.
- •3.7.Означення генеральної та вибіркової середньої, довести...
- •3.8.Означення генеральних та вибіркових дисперсій та середнього квадр відхилення, формули
- •3.9.Дати озн вибіркових: Моди, медіани , початкового моменту, центрального моменту, асиметрії, ексцесу.
- •3.10.Означення точкової та інтегральної оцінки параметра, точність, надійність, інтервальна оцінка, надійний інтеграл
- •3.11.Вивести формули обч кінців надійного інтервалу для оцінки мат сподівання нормального розподілу: з відомим значенням а та з невідомим значенням а. Сформ взаємозалежності.
- •3.13.Записати формули для обчислення кінців надійного інтервалу для оцінки середнього квадратичного відхилення нормального розподілу. Пояснити зміст позначень.
- •3.14.Дати означення емпіричної та теоретичної частот, формули для обч теоретичних частот розподілів : Пуассона, нормальної та генеральної сукупності
- •3.15.Дати озн функціональної, статистичної, кореляційної залежності, умовного середнього, вибіркових рівняння та лінії регресії.
- •3.16.Вивести формули для обч параметрів вибіркового рівн лінійної регресії : а) за не згрупованими даними, б) за згрупованими
- •3.17.Записати формулу для обч вибіркової кореляції кінців надійного інтервалу для інтерн. Оцінки коеф кореляції нормально розподіленої ген сукупності
- •3.18.Дати озн статист гіпотези, назв осн види, означ нульової, альтернативної гіпотез, помилки 1 і 2 роду
- •3.19.Означення статистичного критерію, спостереженого та теор значенню критерію, Крит обл., обл. Прийняття гіпотези, критичних точок, однобічної та двобічної Крит обл., лівоб та правоб крит обл
- •3.20.Дати озн рівня значущості, потужності критерії. Способи знах одноб та двоб критичної обл.
3.8.Означення генеральних та вибіркових дисперсій та середнього квадр відхилення, формули
Генеральною
середньою Dг
наз середнє арифметичне квадратів
відхилень значень ознак генеральної
сукупності від їх середнього значення.
Вибірковою дисперсією DB називають
середню квадратів відхилення варіант
від вибіркової середньої з врахуванням
відповідних частостей
![]() .
Вибірковим середньоквадратичним
відхиленням (стандартом) називають
квадратний корінь із вибіркової
дисперсії. Вибіркова дисперсія дає
занижені значення для дисперсії D
(X) генеральної сукупності, вона буде
зсунутою оцінкою D(Х). Тому вибіркову
дисперсію доцільно виправити таким
чином, щоб вона стала незсунутою
оцінкою.
.
Вибірковим середньоквадратичним
відхиленням (стандартом) називають
квадратний корінь із вибіркової
дисперсії. Вибіркова дисперсія дає
занижені значення для дисперсії D
(X) генеральної сукупності, вона буде
зсунутою оцінкою D(Х). Тому вибіркову
дисперсію доцільно виправити таким
чином, щоб вона стала незсунутою
оцінкою.
вібіркова дисперсия
Dв наз. Середню квадратів відхилення
варіант від вибіркової середньої з
врахуванням відповідних частостей.
![]() .Виправлене
середньоквадратичне відхилення s=
.Виправлене
середньоквадратичне відхилення s=
![]()
3.9.Дати озн вибіркових: Моди, медіани , початкового моменту, центрального моменту, асиметрії, ексцесу.
мода- значения
варіанти, яка має найбільшу частоту.![]()
медіана значення
змінюваної ознаки, яке ділить множину
даних навпіл, так що одна половина
значень більша від медіани, а друга –
менша.

Початковий момент
середнє знач. К-го степення різниці
хі-с, при с=0
![]() *k=
*k=![]()
центральний момент
середнє знач. К-го степення різниці
хі-с, при с=![]() М[(X-mk)k]=
М[(X-mk)k]=![]() k
k
асиметрія:
![]() ,де
m3-централ. емпіричний момент 3-го порядку.
,де
m3-централ. емпіричний момент 3-го порядку.
Ексцес: ек=m4/![]() ,
m4- централ. емпіричний момент 4-го порядку.
,
m4- централ. емпіричний момент 4-го порядку.
3.10.Означення точкової та інтегральної оцінки параметра, точність, надійність, інтервальна оцінка, надійний інтеграл
точковими оцінками параметрів розподілу генеральної сукупності наз. Такі оцінки, які визначаються одним числом.
Інтервальна оцінка та , що визначається 2 числами – кінцями інтервалу.
Надійністю оцінки
параметрів 0 за 0* наз. імовірність
![]() з якою викон. нерівність
з якою викон. нерівність
![]()
Інтервал (0* -
![]() )=
)=![]() наз. надійним, якщо він покриває невідомий
параметр 0 із заданою надійністю
наз. надійним, якщо він покриває невідомий
параметр 0 із заданою надійністю
![]() .
.
Точність оцінки
визнач.
![]() .
.
![]()
![]()
![]()
3.11.Вивести формули обч кінців надійного інтервалу для оцінки мат сподівання нормального розподілу: з відомим значенням а та з невідомим значенням а. Сформ взаємозалежності.
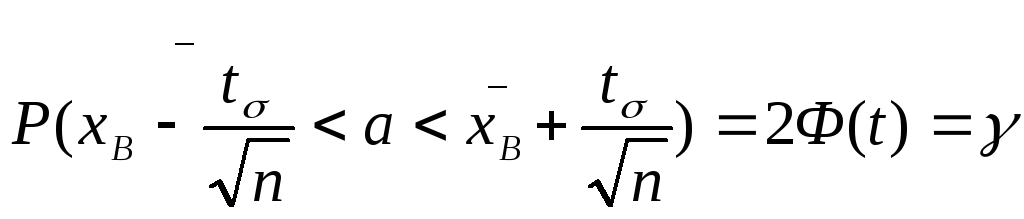 ,
тобто з надійністю
,
тобто з надійністю
![]() довірчий інтервал (
довірчий інтервал (![]() )
покриває невідомий параметр а. точність
оцінки буде
)
покриває невідомий параметр а. точність
оцінки буде
![]()
Число t визначається
рівністю 2Ф(t)=
![]()
![]() Ф(t)=
Ф(t)=
![]() .
.
При зростанні
об’єму вибірки число![]() зменш.,
а це знач., що точність оцінки збільш.
Коли надійність збільш.
зменш.,
а це знач., що точність оцінки збільш.
Коли надійність збільш.
![]() ,
ф-ція Ф(t) зростає. Збільшення надійності
зменш. її точність.
,
ф-ція Ф(t) зростає. Збільшення надійності
зменш. її точність.
3.13.Записати формули для обчислення кінців надійного інтервалу для оцінки середнього квадратичного відхилення нормального розподілу. Пояснити зміст позначень.
Інтервальною оцінкою середнього квадратичного відхилення σ нормально розподіленого кількісної ознаки Х по “виправленому” вибірковому середньому квадратичному відхиленню s є довірчий інтервал
s(1 – q)< σ<s (1+q) при q<1
0< σ < s (1+q) при q>1 ,
де
q знаходять
по
табл.
за
заданими
n і
![]() ;
n – об’єм
вибірки,
;
n – об’єм
вибірки,
![]() -
надійність,
з
якою
довірчі
інтервали
покривають
параметр
σ.
Для
цього
повинно
виконуватись
рівність
P(|σ
– s|<
-
надійність,
з
якою
довірчі
інтервали
покривають
параметр
σ.
Для
цього
повинно
виконуватись
рівність
P(|σ
– s|<![]() )=
)=![]() або
P(s -
або
P(s -
![]() <
σ<s+
<
σ<s+![]() )=
)=![]() ;
q=
;
q=![]() /s
/s
