10.7.1. Метод парабол с использованием симметричной точки

Одним из предложений по ускорению сходимости метода парабол является вариант метода с использованием симметричной точки. У него, начиная со второй итерации по найденной при помощи квадратичной аппроксимации точке x_min (которая принимается в качестве новой промежуточной точки: x₂ = x_min) из имеющихся точек a,с,b выбирается ближайшая, а третья рассчитывается симметрично ей относительно x_min. На рис.10.16 показан случай, когда ближайшей к х_min является точка с и х_min < с .

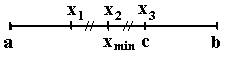
Рис. 10.16

Данная модификация метода, как и исходный метод парабол, требует учета всех возможных вариантов поведения функции. В противном случае не обеспечивается гарантированная сходимость решения к искомой внутренней точке исходного доверительного отрезка.

При применении алгоритмов, обеспечивающих получение искомого решения, метод с использованием симметричной точки в ряде случаев дает наиболее быструю сходимость по сравнению с другими вариантами метода парабол. Однако в некоторых случаях скорость сходимости резко ухудшается – в десятки и даже сотни раз, что позволяет характеризовать данный вариант метода парабол как нестабильный.

10.7.2. Универсальный алгоритм метода парабол

Для практической реализации метода парабол может быть использован следующий алгоритм, пригодный для любых непрерывных унимодальных функций, в том числе – негладких, имеющих точки излома на доверительном отрезке. Назовем его универсальным.

Исходные данные:

1) [a,b] – границы начального доверительного отрезка,

2) с - промежуточная точка, a<c<b,

3) F(a),F(c),F(b) - значения F(x) в точках a,b,с,

4)  - точность.

Выходные данные:

1) [a,b] – новые сокращенные границы исходного доверительного отрезка, b-a< ,

Начало цикла по условию (b-a >  ).

Шаг 1. Проверка близости точки с к крайним a,b и соответствующий выбор новой пробной точки (отрыв точки с от краев доверительного отрезка).

Если (с-a)/(b-a) < 0,1; то x_min:= с + (b-с)/4, переход на Шаг 7.

Если (b-с)/(b-a) < 0,1; то x_min:= с - (с-а)/4, переход на Шаг 7.

Шаг 2. Расчет величины старшего коэффициента C₂ по формуле (10.4 б). В зависимости от выполнения условия C₂ = 0 переход на Шаг 3 либо 4 .

Шаг 3. C₂=0. Аппроксимирующая парабола вырождается в прямую линию, при этом целевая функция может не совпадать с данной прямой на всем отрезке [a,b]. В этом случае обычные формулы не применимы.

При F(a) < F(b): x_min:=(a+с)/2, b:=c; иначе: x_min:=(b+c)/2, а:=c. F_min = F(x_min). Переход на конец цикла .

Шаг 4. C₂  0. Аппроксимирующая кривая является параболой. Расчет величины x_экстр по формуле (10.4 а). В зависимости от выполнения условий C₂ < 0 , C₂ > 0 переход на Шаг 5 либо 6.

Шаг 5. C₂<0. Ветви параболы направлены вниз – в точке x_min достигается локальный максимум.

При x_экстр< (а+b)/2 : x_min:=(b+c)/2, а:=c; иначе: x_min:= (a+ с)/2, b:=c. F_min = F(x_min). Переход на конец цикла.

Шаг 6. C₂>0. Ветви направлены вверх, в точке x_экстр достигается локальный минимум.

Проверка нештатных ситуаций и соответствующие действия.

1. Уход точки x_экстр с отрезка [a,b]:

а) при x_экстр  а: {x_min:=(a+с)/2; b:=c; F_min = F(x_min); переход на конец цикла};

б) при x_экстр  b: {x_min:=(b+c)/2; a:=c; F_min = F(x_min); переход на конец цикла}.

2. Попадание точки x_экстр в промежуточную точку c (данная ситуация возникает, например, уже на втором шаге, если F(x) сама является квадратичной параболой). Если x_экстр - c< /2, то:

а) при x_экстр < c, x_экстр  c: x _min = c – /2.

б) при x_экстр > c, x_экстр  c: x _min = c + /2.

x_min:= x_экстр. (присваивание будет выполнено, если не выполняются условия 1 и 2).

Шаг 7. Расчет значения функции в точке x_min: F_min = F(x_min).

Сокращение доверительного интервала.

Если x_min< c, то при F_min<F(c): b:=c, c:=x_min; иначе: а:=x_min .

Если x_min c, то при F_min<F(c): а:=c, c:=x_min; иначе: b:=x_min .

Конец цикла.

Завершение поиска.

Описанный универсальный алгоритм позволяет применять метод парабол наряду с регулярными методами для минимизации любых унимодальных функций.

Пример 1. Найти минимум функции F(х) = 2х³- 3х² на интервале [0,2; 2] при помощи универсального алгоритма метода парабол с заданной внутренней точкой интервала с = 0,4 при точности  = 0,5.

Решение. При последовательном выполнении шагов переходы к ним не оговариваются.

Шаг 0. Предварительные действия. Рассчитываем значения функции в точках a,b,c: F(a) = -0,10; F(с) = -0,35; F(b) = 4.

Цикл по условию ( b-a >  ).

Итерация 1. Шаг 1. Условия (с-a)/(b-a) < 0,1 и (b-с)/(b-a) < 0,1 не выполняются.

Шаг 2. Расчет C₂. C₂ = [(F(b)-F(a))/(b-a) - (F(c)-F(a))/(c-a)] / (b-c) = [(4)/(1,8) - (-0,25)/ (0,2)]/ (1,6) = 2,2. Переход на Шаг 4.

Шаг 4. x_экстр = 0,58. Так как С₂>0, то переход на Шаг 6.

Шаг 6. Точка x_экстр не выходит за пределы отрезка [a,b] и не близка к средней точке c, поэтому x_min:= x_экстр.

Шаг 7. Расчет значения функции в точке x_min: F_min = F(x_min)= -0,62. Сокращение доверительного интервала. Так как x_экстр  c и F_min <F(c), то а:=c=0,4; c:=x_min=0,58.

Итерация 2. Шаг 1. Условия не выполняются.

Шаг 2. C₂ =2,96 > 0. Переход на Шаг 4.

Шаг 4. x_экстр = 0,74. Переход на Шаг 6.

Шаг 6. Условия 1 и 2 не выполняются, x_min:= x_экстр.

Шаг 7. F_min = F(x_min)= -0,83.

Так как x_min  c и F_min< F(c), то а:=c=0,58; c:=x_min=0,74.

Итерация 3. Шаг 1. Условия не выполняются.

Шаг 2. C₂ = 3,66 > 0. Переход на Шаг 4.

Шаг 4. x_экстр = 0,84. Переход на Шаг 6.

Шаг 6. Условия 1 и 2 не выполняются, x_min:= x_экстр.

Шаг 7. F_min = F(x_min) = -0,93. Так как x_min  c и F_min < F(c), то а:=c=0,74; c:=x_min=0,84.

Итерация 4. Шаг 1. Так как (с-a)/(b-a)=(0,1)/(1,16) < 0,1, то: x_min:= с + 0,25 (b-с)/2 = 1,13. Переход на Шаг 7.

Шаг 7. F_min = F(x_min)= -0,94. Так как x_min  c и F_min < F(c), то а:=c=0,84; c:=x_min=1,13.

Итерация 5. Шаг 1. Условия не выполняются.

Шаг 2. C₂ = 4,95 > 0. Переход на Шаг 4.

Шаг 4. x_экстр = 0,99. Переход на Шаг 6.

Шаг 6. Условия 1 и 2 не выполняются, x_min:= x_экстр.

Шаг 7. F_min = F(x_min) = -0,9998. Так как x_min< c и F_min<F(c), то b:=c=1,13; c:=x_min=0,99.

Поскольку (b-а) = 0,29 < , то цикл завершается.

Ответ: Выполнено 5 итераций, вычислено 8 значений функции, найден доверительный интервал [0,84;1,13].

Рассмотренный вариант метода парабол при масштабах порядка 10² – 10³ и выше в среднем работает быстрее метода Фибоначчи – наиболее быстрого регулярного метода. Поскольку сам он не является регулярным, для него в общем случае не может быть получено оценок скорости сходимости без наложения дополнительных условий на характер целевой функции.