Глава 12. Численное решение обыкновенных дифференциальных уравнений
12.1. Общие понятия теории оду. Их численные решения
Обыкновенными дифференциальными уравнениям (ОДУ) называют такие уравнения, которые содержат одну или несколько производных от искомой функции у(x). Порядком ОДУ называют максимальный порядок входящей в него производной неизвестной функции у(x). В общем виде ОДУ можно представить в следующем виде:
F(x,y,y,y,…,y(n)) = 0, (12.1)
где x – независимая переменная, y(i)- i-ая производная от искомой функции у(x) (y = y(0)), n - порядок уравнения.
К решению того или иного ОДУ или системы ОДУ сводится решение многих задач в науке и технике, в которых учитываются временные или пространственные изменения некоторой функции.
В качестве стандартной формы записи ОДУ принят такой вид их представления, при котором старшая производная выражена из левой части (12.1) в явном виде:
y(n) =F(x,y,y,y,…,y(n-1)). (12.2)
Эту форму записи ОДУ называют уравнением, разрешенным относительно старшей производной.
Линейным дифференциальным уравнением называют уравнение, линейное относительно неизвестной функции y(x) и всех ее производных. В таком уравнении отсутствуют вторые степени y(x) и ее производных, их произведения и т.д.
Общим решением ОДУ (12.1) называют любую функцию у(x), которая обращает выражение (12.1) в тождество на заданном конечном отрезке или бесконечном интервале. Сам процесс решения дифференциального уравнения называют интегрированием дифференциального уравнения.
Общее решение ОДУ n–го порядка содержит n произвольных постоянных (констант) C1,C2,…,Cn, т.е. его можно представить в виде:
у(x) = f(x,C1,C2,…,Cn). (12.3)
Появление констант является следствием выполнения операции интегрирования, когда неопределенный интеграл находится в виде суммы первообразной подынтегрального выражения и константы интегрирования.
Частное решение ОДУ получается из общего при задании константам интегрирования конкретных числовых значений, которые находятся по дополнительным условиям. Для получения единственного частного решения ОДУ (12.1) необходимо задать n дополнительных условий.
Под точным (аналитическим) решением (общим или частным) ОДУ понимают получение искомого его решения (функции y(x)) в виде аналитического выражения, содержащего элементарные функции. Однако практическое определение аналитического решения возможно далеко не всегда, даже для уравнений относительно простого вида.
Численное частное решение ОДУ (12.2), разрешенного относительно старшей производной, заключается в численном расчете значений искомой функции y(x) и ее производных в некоторых заданных точках {x1, x2,…, xN}, лежащих на области определения х. Практически решение ОДУ n-го порядка вида имеет вид таблицы значений, содержащей столбцы {x,y,y,y,…,y(n-1))}, в каждой строке которой содержится значение xi и соответствующие величины y(xi),y(xi),y(xi),…,y(n-1)(xi). Столбец значений старшей производной y(n) при необходимости вычисляется подстановкой значений {x,y,y,y,…,y(n-1))} в левую часть уравнения (12.2). Общий вид таблицы, задающей численное решение ОДУ n-го порядка задает Таблица 12.1.
Таблица 12.1. Численное решение ОДУ n-го порядка
|
X |
y |
y' |
|
y(n-1) |
|
x1 |
y(x1) |
y'(x1) |
… |
y(n-1)(x1) |
|
x2 |
y(x2) |
y'(x2) |
… |
y(n-1)(x2) |
|
|
|
|
|
|
|
xN |
y(xN) |
y'(xN) |
… |
y(n-1)(xN) |
Для ОДУ первого порядка таблица, задающая его численное решение, имеет только два столбца со значениями {xi,y(xi)}.
Множество значений независимого переменного {x1, x2,…, xN}, в которых определяются значения функции и ее производных y(xi),y(xi),y(xi),…,y(n-1)(xi), называют сеткой. Отдельные значения xi называют узлами сетки. Обычно применяют равномерные сетки, в которых разница между соседними узлами постоянна и называется шагом сетки или шагом интегрирования дифференциального уравнения: h= xi+1 - xi, I = 1,2,…,N.
В зависимости от способа задания n дополнительных условий, которые необходимы для определения частного решения ОДУ n–го порядка существуют два различных типа задач:
1) задача Коши и
2) краевая задача.
Если дополнительные условия задают в одной точке, то такую задачу называют задачей Коши. Дополнительные условия в задаче Коши называют начальными условиями, поскольку их обычно задают в начальной (во времени или пространстве) точке области изменения независимого параметра уравнения.
Если же дополнительные условия задают более чем в одной точке, т.е. при различных значениях независимой переменной х, то такую задачу называют краевой, а сами дополнительные условия называют краевыми или граничными.
Очевидно, при n = 1 можно говорить только о задачи Коши. А краевые задачи существуют для ОДУ не ниже 2-го порядка.
Примеры 1 постановок задачи Коши:
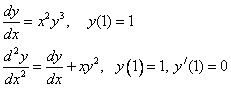
Примеры 2 постановок краевых задач:
