12.6. Численные методы решения систем оду первого порядка

Методы решения одиночных дифференциальных уравнений первого порядка могут быть также использованы для решения систем данных уравнений. В процессе решения системы в отличие от одиночного, необходимо пересчитывать значения не одной, а нескольких функций.

Представим систему двух уравнений первого порядка в следующем виде:

dу(x)/dx = ( x, у, z),

dz(x)/dx =  ( x, у, z),

у(x₀) = у₀, z(x₀) = z₀. (12.23)

Неизвестными в задаче (12.23) являются две функции у(x) и z(x), зависящие от одного общего независимого параметра х. Поскольку в общем случае производные dу(x)/dx и dz(x)/dx зависят от обеих неизвестных функций у(x) и z(x), то систему нельзя решить отдельно относительно у(x) и отдельно относительно z(x). Решение должно определяться в результате совместного интегрирования обеих неизвестных функций. При этом обычные методы решения принимают следующий вид.

1. Явный метод Эйлера:

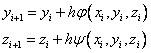(12.24)

2. Метод Хойна (модифицированный метод Эйлера):

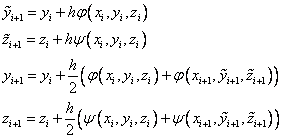(12.25)

3. Схема Рунге – Кутта четвертого порядка точности:

(12.26)

Вопросы для проверки знаний.

1. Какой вид имеет система ОДУ первого порядка, зависящих от одного независимой переменной ?

2. Почему нельзя в общем случае раздельно решить систему двух уравнений первого порядка относительно у(x) и отдельно относительно z(x) ?

3. Как строятся методы решения данных систем ОДУ ?

12.7. Численные методы решения оду и систем оду высоких порядков

Обыкновенное дифференциальное уравнение с неизвестной функцией y(t), в которое входят производные этой функции вплоть до y^(N) (t), называются ОДУ N-го порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши требуется задать N начальных условий на саму функцию y(t) и ее производные от первого до (N-1)-го порядка включительно. Для решения задач Коши для ОДУ высших порядков можно использовать прямые методы, а также сводить их к системам уравнений первого порядка.

Рассмотрим в общем виде задачу Коши для уравнения второго порядка относительно функции у(x):

d²у/dx² = f(x, у, dу/dx),

у(x₀) = у₀, dу/dx(x₀) = z₀. (12.27)

Если использовать метод сведения к системе уравнений первого порядка, то необходимо ввести вторую неизвестную функцию z(x)=dу/dx. Тогда задача Коши (12.27) второго порядка для одной функции у(x) будет заменена следующей эквивалентной системой из двух уравнений первой степени относительно двух функций у(x) и z(x):

dу/dx = z(x),

dz/dx = f(x, у, z),

у(x₀) = у₀, z(x₀) = z₀. (12.28)

Полученная система (12.28) представляет собой частный случай общей задачи (12.23) при (x,у,z) = z(x), (x,у,z) = f(x, у, z).

Пример. Найти численное решение задачи Коши для уравнения второго порядка:

d²у/dx² + 2dу/dx+ у(x) = x, у(0) = 1, dу/dx(0) = 0

на отрезке [0,1] с шагом h = 0,2 а) явным методом Эйлера, б) методом Хойна (модифицированным методом Эйлера) и в) методом Рунге – Кутта. Результаты расчетов сравнить с точным решением: у(x) = 3e^-x +2xe^-x +x - 2.

Введем функцию z(x)=dу/dx. Тогда получим эквивалентную задачу Коши для системы двух ОДУ первого порядка:

dу/dx = z(x),

dz/dx = x - 2dу/dx - у(x) = x - 2z(x) - у(x),

у(0) = 1, z(0) = dу/dx(0) = 0.

Расчетные схемы (12.24)-(12.26) принимают следующий вид.

1. Явный метод Эйлера:

2. Метод Хойна (модифицированный метод Эйлера):

3. Метод Рунге – Кутта:

Узловые значения x_i, точные значения (y_тi) функции у(x), результаты расчета по явной схеме Эйлера (y_т,y₁,z₁,y₁=y_т-y₁), а также по методу Хойна (y₂,z₂,y₂=y_т-y₂) приведены в Таблице 12.3.

Таблица 12.3. Результаты расчета по явной схеме Эйлера и методу Хойна

xi	yтi	y1i	z1i	y1i	y2i	z2i	y2i
0	1	1	0	0	1	0	0
0.2	0.983685	1	-0.2	0.016315	1	-0.18	0.016315
0.4	0.947216	0.96	-0.28	0.012784	0.962	-0.244	0.014784
0.6	0.905009	0.904	-0.28	0.001009	0.9096	-0.2314	0.004591
0.8	0.866913	0.848	-0.2288	0.018913	0.85846	-0.17048	0.008453
1	0.839397	0.80224	-0.14688	0.037157	0.818532	-0.08127	0.020865

Результаты расчета по cхеме Рунге - Кутта (x_i, y_тi, k_1i - k_4i, y_3i, y₃=y_тi - y_3i) приведены в Таблице 12.4.

Таблица 12.4. Результаты расчета по cхеме Рунге - Кутта

xi	yтi	k1i	k2i	k3i	k4i	y3i	y3i
0	1	0	-0,1	-0,07	-0,15	1	0
0,2	0,9836	-0,1462	-0,1953	-0,1740	-0,2094	0,9635	0,0201
0,4	0,9472	-0,2065	-0,2199	-0,2050	-0,2095	0,9213	0,0259
0,6	0,9050	-0,2073	-0,1963	-0,1865	-0,1698	0,8832	0,0218
0,8	0,8669	-0,1682	-0,1412	-0,1350	-0,1048	0,8557	0,0112
1	0,8394	-0,1036	-0,0668	-0,0631	-0,0249	0,8428	-0,0034

При решении систем ОДУ N-го порядка, у которых максимальный порядок уравнений равен N, используется тот же принцип, что и для отдельных уравнений - сведение их к системам уравнений первого порядка.

Вопросы для проверки знаний.

1. Какое дифференциальное уравнение называют ОДУ N-го порядка ?

2. Какие начальные условия должны быть заданы в начальной точке для корректной постановки задачи Коши с ОДУ N-го порядка ?

3. Какие два основных способы можно применить для решения задачи Коши с ОДУ N-го порядка ?

4. Как задачу Коши для уравнения второго порядка приводится к эквивалентной системе с двумя линейными ОДУ ?