30

10. Численные методы однопараметрической оптимизации

Теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, направленных на поиск наилучшего варианта из множества возможных альтернатив. Она широко применяется в науке для оптимизации методов исследований, в технике для поиска наилучших вариантов конструкций объектов, а также в других областях человеческой деятельности.

10.1. Однопараметрические задачи оптимизации. Классификация. Основные термины

Практически задача оптимизации сводится к поиску экстремума (минимума или максимума) некоторой функции, которая выражает суммарное качество рассматриваемого объекта оптимизации. Такую функцию называют целевой. Переменные целевой функции, которые можно варьировать в некоторой допустимой области , называют управляемыми параметрами.

Среди характеристик, определяющих математическую формулировку задач оптимизации и методы их решения, можно выделить следующие:

1.Число управляемых параметров.

2. Наличие либо отсутствие ограничений на область  изменения управляемых параметров.

Однопараметрической называют задачу оптимизации с одним управляемым параметром. Они имеют вид:

F(x) max, F(x) min .

х х

Первый вид задач сокращённо называют максимизацией, второй – минимизацией.

В условных одномерных задачах наиболее распространённым видом ограничений является система неравенств {x a,x b} , задающая принадлежность параметра задачи x некоторому отрезку [a,b]. Группу методов, решающих задачу поиска экстремума функции F(x) на отрезке [a,b]. будем называть одномерным поиском на доверительном отрезке.

Важнейшей безусловной задачей одномерной оптимизации является также поиск ближайшего к заданной точке x₀ минимума функции F(x) в направлении её убывания. Область поиска потенциально не ограничена. Назовём группу методов, решающих эту задачу, одномерным поиском в окрестности точки.

Помимо самостоятельного значения практическая ценность методов одномерной оптимизации заключается в том, что они являются основой для построения многопараметрических методов.

По способу поиска требуемого экстремума методы решения задач оптимизации делят на аналитические (называемые также классическими), которые основаны на дифференциальном исчислении, и на численные - основанные на полном переборе или итерационном расчете и последующем анализе значений функции.

Численные методы применяют тогда, когда целевая функция F(x) имеет сложное аналитическое выражение либо вычисляется при помощи алгоритма, т.е. не имеет формульного выражения.

Точностью метода определения экстремума называют максимально возможную длину доверительного интервала [, ], на котором после завершения поиска размещается точное оптимальное значение аргумента х_опт. Обозначим точность через  :  =  -  .

Масштабом задачи M будем называть отношение длины исходного доверительного интервала [a,b] к величине необходимой гарантированной точности  : M = (b-a)/.

При заданном методе масштаб задачи, а также форма графика целевой функции F(x) на [a,b] определяют число n необходимых вычислений F(x) в процессе её оптимизации: n = n (M,F(x)).

Основное условие, которому должен удовлетворять численный метод оптимизации - сходимость получаемого решения к точному значению искомого экстремума (локального или глобального). При наличии сходимости главным качественным показателем численного последовательного метода является скорость сходимости, которую обычно оценивают числом n вычислений целевой функции F(x) (реже - числом итераций), необходимых для получения искомого решения с заданной точностью .

Точки, в которых вычисляются значения функции в процессе поиска ее экстремума, называют пробными.

Численные методы поиска экстремума при заданном исходном доверительном отрезке [a,b] и требуемой точности  всегда требуют выполнения следующих действий.

1. На отрезке [a,b] определяется множество пробных точек {x_i} = { x₁, ..., x_n}.

2. В них рассчитываются значения функции {F(x₁), ... , F(x_n)}.

3. В качестве итогового доверительного отрезка принимают найденный отрезок длины  , содержащий искомое решение.

Наряду с пробными точками рассмотрим множество узлов, в которое наряду с {x_i} включаем крайние точки доверительного отрезка a (если x₁  a ) и b (если x_n  b ). Общее число узлов обозначим через N. В отличие от пробных точек их будем обозначать через у_k.

Допустим, необходимо определить минимум функции F(x) на доверительном отрезке [a,b]. F(x) называется унимодальной на [a,b], если она:

- непрерывна,

- существуют числа  и   [a,b] (а      b) такие, что:

на участке [a,] F(x) строго убывает;

на участке [,] F(x) строго постоянна;

на участке [,b] F(x) строго возрастает.

Если функция F(x) унимодальна на [a,b] и  = , то она называется строго унимодальной.

На рис. 10.1 и 10.2 даны примеры унимодальной и строго унимодальной функций.

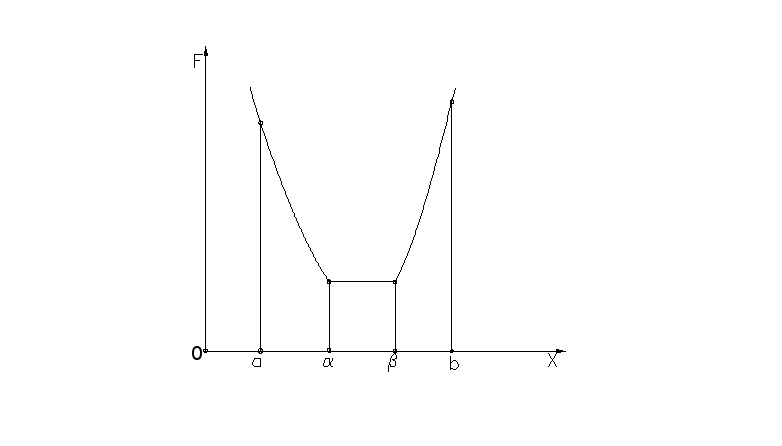
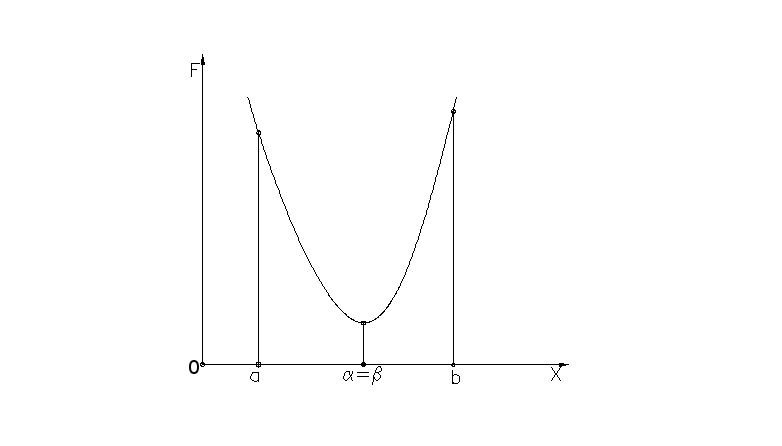
Рис. 10.1 Рис.10.2

Численные однопараметрические методы полностью определяются алгоритмами задания пробных точек. Рассмотрим основные характеристики таких методов и их классификацию.

1. Возможность применения на областях, содержащих один или несколько экстремумов. Методы могут быть универсальными (предназначенными для поиска глобального минимума для функций со многими локальными экстремумами) и локальными (для использования на унимодальных функциях, имеющих один экстремум на выделенной области поиска).

2. Наличие ограничений (вид области определения) целевой функции. Наиболее распространёнными типами области определения являются:

а) ограниченный отрезок [a,b] ,

б) вся числовая ось (-, ) .

3. Способ выбора пробных точек. Пассивными называют такие методы, в которых полный набор пробных значений параметра {x_i} = {x₀, x₁, ..., x_n} назначается до начала вычислений. Последовательными называют итерационные методы поиска, в которых при поиске на доверительном отрезке:

1) пробные точки {x_i}, кроме начальных, выбираются последовательно после анализа значений функции на предыдущих шагах;

2) доверительный интервал [а_k, b_k], содержащий точку экстремума, также уточняется на каждом шаге k.

Комбинированными называют методы, сочетающие различные виды поиска.

4. Максимальная степень используемых производных. Порядком метода называют максимальную степень производных, используемых в его расчетах. Если производные не используются, а только значения функции, то порядок будет нулевым, поскольку данные значения являются производной нулевой степени.

Как правило, оптимальной стратегией поиска глобальных экстремумов является комбинированная, которая сходна с поиском корней уравнений и заключается в следующем:

1) просмотр области при помощи пассивного или последовательного метода, выделение участков, содержащих локальные экстремумы;

2) последующее уточнение локальных экстремумов последовательным методом;

3) выбор глобального экстремума из найденных локальных.

Каждый теоретически верный численный метод поиска экстремума при высоких требованиях к точности решения  в процессе практического расчета на ЭВМ по правильной программе может зациклиться, выдать неверные значения либо работать недопустимо долго при отсутствии учета точности представления чисел в ЭВМ. Поэтому величину  в практических расчетах необходимо согласовывать с точностью, которую обеспечивает заданный формат представления чисел.

Вопросы для проверки знаний.

1. Какую функцию называют целевой ? Что называют ее управляемыми параметрами ?

2. Какие задачи оптимизации называют однопараметрическими ?

3. Чем отличаются одномерные поиск на доверительном отрезке и поиском в окрестности точки ?

4. На какие группы делят методы решения задач оптимизации по способу поиска требуемого экстремума ?

5. Какие точки называют пробными ?

6. Каковы главные качественные показатели численных методов оптимизации ?

7. Какие основные действия выполняются в численных методах поиска экстремума при заданном исходном доверительном отрезке [a,b] и требуемой точности  ?

8. Какие целевые функции называют унимодальными, а какие - строго унимодальными ?

9. На какие группы делят численные методы поиска экстремума, исходя из их возможности поиска глобальных и локальных экстремумов функций ?

10. Какие виды области определения целевых функций обычно рассматривают в задачах одномерной оптимизации ?

11. На какие группы делят численные методы поиска экстремума по способу выбора пробных точек ?

12. Что называют порядком численных методов поиска экстремума ?

13. Какова оптимальная стратегия поиска глобальных экстремумов ?