10.3. Последовательные регулярные методы. Дихотомия

В последовательных методах все пробные точки, кроме начальных, выбираются последовательно после анализа значений функции на предыдущих шагах. Также последовательно сокращается доверительный интервал.

В зависимости от характера выбора пробных точек и способа изменения длины доверительного интервала последовательные методы можно разделить на регулярные и аппроксимационные.

Регулярными назовем такие последовательные методы, у которых длина сокращаемых частей доверительного интервала не зависит от целевой функции, а определяется только выбранным методом оптимизации.

Аппроксимационными назовем последовательные методы, у которых выбор новых пробных точек осуществляется путем аппроксимации целевой функции по её ранее найденным пробным точкам. При этом длина сокращаемой части интервала зависит не только от метода оптимизации, но и от вида рассматриваемой целевой функции.

Рассмотрим алгоритм одного из наиболее простых регулярных последовательных методов, называемого дихотомией. Допустим, решается задача минимизации унимодальной функции F(x) на доверительном отрезке [a,b] с заданной точностью .

Предварительные действия (Шаг 0).

1. Доверительный интервал принимают равным исходному: а₀ = а , b₀ = b.

2. Выбираем некоторое малое число 0 <.

Шаг i (i>0). Действия выполняются в цикле при выполнении условия (b_i-1-a _i-1 >).

1. Выбираем точки

; ;

лежащие около средней точки (a_i-1+b_i-1)/2 доверительного интервала [a_i-1,b_i-1], найденного на предыдущем шаге i-1 .

2. Расчет значений F(x₁) и F(x₂).

3. Проверка F(x₁), F(x₂) и коррекция интервала.

а) . Точка минимума расположена между х₂ и b_i-1 (рис.10.8) либо между х₁ и х₂ (рис.10.9).

Рис. 10.8 Рис. 10.9

В этом случае принимают: a_i = х₁ , b_i = b_i-1, отбрасывают отрезок (a_i-1 , х₁ ).

б) F(х₁) < F(х₂). Точка минимума расположена между а_i и х₁ (рис.10.10) либо между х₁ и х₂ (рис.10.11). Новые границы доверительного интервала: a_i = a_i-1, b_i = х₂ . Отбрасывают участок (х₂, b_i-1).

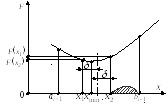
Рис. 10.10 Рис. 10.11

После завершения работы метода, когда найден итоговый доверительный интервал [a_k ,b_k], длина которого b_k - a_k  .

Метод является последовательным, поскольку пробные точки, необходимые для поиска оптимального значения аргумента, определяются не все сразу, а парами – на каждом шаге k после анализа значений целевой функции F(х) на предыдущем шаге k-1.

Как нетрудно заметить, на каждом шаге выбор пробных точек осуществляется в соответствии с -оптимальным пассивным методом для случая чётного числа точек n=2, что позволяет, как показано в Примере 2 п. 10.2, максимально приблизиться к минимальной предельной гарантированной точности _min = (b - a) /2.

Для оценки оптимальности метода необходимо найти для него зависимости (n) и n() . В отличие от п.10.2, где исследовалось одновременно всё множество пассивных методов, выше рассмотрен один метод, в котором зафиксирован способ задания пробных точек.

Длина доверительного интервала [a₁ ,b₁] связана с начальной длиной [a₀,b₀] следующим образом: b₁ - a₁ =(b₀ - a₀)/ 2+  . Зависимость можно представить в виде:

b₁ - a₁ - 2 = (b₀ - a₀ - 2) / 2 .

Рассуждая аналогично, получим, что для произвольного шага k длина доверительного интервала:

b_k - a _k - 2 = (b₀ - a₀ - 2) / 2^k = (b - a - 2) / 2^k .

После завершения процесса выполняется неравенство

b_k - a_k = (b - a - 2) / 2^k + 2   .

Отсюда следует, что номер шага k , на котором достигается требуемая точность  , равен

k() =] log ₂ (b - a - 2)/( - 2)[ ,

где ][ означает ближайшее целое сверху к значению выражения, заключённого в скобки.

Поскольку n_ш=2 (на каждом шаге всегда вычисляется два значения целевой функции), то полное число необходимых вычислений F(х):

п() = n_ш k() = 2]log ₂ (b - a - 2)/( - 2)[ .

Обратную зависимость  (п) находим из равенства

(b - a - 2) / 2^k + 2 = с учётом п = 2k:

 (п) = (b - a - 2) / 2 ^0.5n + 2 .

При асимптотические скорости роста зависимостей  (n) и n () для дихотомии принимают следующий вид:

 (n) = O[(b-a)/2^0.5n];

n() =O[2log₂(b - a)/] =O[2log₂М].

Метод работает значительно быстрее пассивных, поскольку на каждом шаге после вычисления двух значений функции доверительный интервал сокращается почти в два раза. Однако он, в отличие от пассивных методов, всегда находит глобальный минимум только для унимодальных функций. Метод дихотомии является регулярным, поскольку сокращаемая на каждом шаге часть доверительного интервала не зависит от рассматриваемой функции.

Пример 1. Найти минимум функции F(х) = х²–2х на интервале [0,2;2] по методу дихотомии при заданной гарантированной точности  =0,5 и величине  = 0,05.

Решение.

Шаг 1. Координата средней точки исходного доверительного интервала равна (0,2+2)/2=1,1. Пробные точки: x₁=1,1-0,05=1,05; x₂=1,1+0,05=1,15. Значения функции в них: F(x₁)=-0,9975; F(x₂)=-0,9775.

Поскольку F(x₁)<F(x₂), то отбрасываем часть доверительного интервала [x₂; b]. Получаем новый интервал [а₁;b₁]= [0,2; 1,15]. Его длина b₁-а₁=0,95>=0,5; поэтому поиск необходимо продолжить.

Шаг 2. Средняя точка доверительного интервала имеет координату (0,2+ 1,15)/2 = 0,675. Пробные точки: x₁=0,675-0,05=0,625; x₂=0,675+0,05=0,725. Значения функции в них: F(x₁)=-0,390625; F(x₂)=-0,525625.

F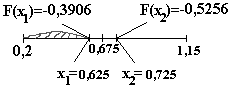(x₁)>F(x₂), поэтому отбрасываем часть доверительного интервала [а₁; x₁]. Новый интервал [а₂; b₂]= [0,625;1,15] имеет длину b₂ - а₂= 0,55> = 0,5; поэтому необходимо выполнить следующий шаг.

Шаг 3. Средняя точка: 0,5(0,625+1,15)=0,8875. Пробные точки: x₁ =0,8875–0,05 = 0,8375; x₂= 0,9375. Значения функции: F(x₁)=-0,70140625; F(x₂)=-0,87890625.

F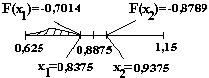(x₁)>F(x₂),поэтому отбрасываем часть доверительного интервала [а₂; x₁].

Полученный интервал [а₃ , b₃] =[0,8375; 1,15] имеет длину b₃-а₃=0,3125<=0,5, поиск завершаем.

Ответ. Для решения задачи методом дихотомии с гарантированной точностью =0,5 и величиной =0,05 выполнено 3 шага, использовано 6 пробных точек. Найден итоговый доверительный интервал [а₃ , b₃] =[0,8375; 1,15] длины 0,3125.

Замечание 1. Хотя в Примере 1 произведен расчет 6 пробных точек, как и в оптимальном пассивном методе, найденная длина итогового доверительного интервала значительно меньше.

Замечание 2. Существенным недостатком метода дихотомии является то, что информация об одной из пробных точек на каждом шаге не участвует в дальнейших вычислениях. Так, в Примере 1 точка x₁=1,05 на Шаге 1 с наилучшим из найденных значений функции F(x₁)=-0,9975 в дальнейшем не участвует в расчетах и информация о ней теряется.

Вопросы для проверки знаний.

1. Чем последовательные методы отличаются от пассивных при выборе пробных точек ?

2. Какие из последовательных методов названы регулярными ?

3. Какие из последовательных методов названы аппроксимационными ?

4. Как осуществляется один шаг по методу дихотомии ?

Практические задания.

Решить по методу дихотомии задачи 1)-13) из п.10.2. Во всех задачах принять = 0,1.