10.4. Метод золотого сечения

Основная идея данного метода – сокращение числа n_ш вычислений функции на каждом шаге (кроме первого) до 1 (минимально возможного значения) с дальнейшим использованием при поиске минимума второй пробной точки каждого шага, которая попадает внутрь нового доверительного интервала. Несмотря на то, что доверительный интервал сокращается при этом существенно менее, чем в два раза (в отличие от дихотомии), данный метод за счёт уменьшения n_ш работает в общем значительно быстрее.

Золотым сечением отрезка [a,b] называется такое его деление промежуточной точкой с, при котором выполняется соотношение (рис 10.12 а), где ξ – коэффициент золотого сечения.

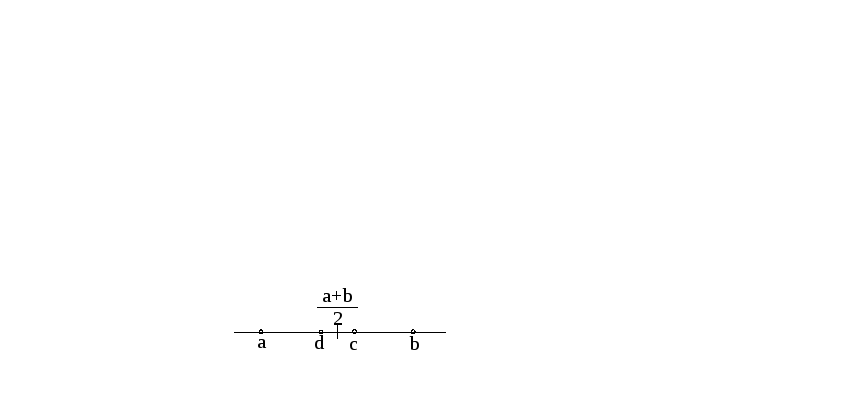
а б

Рис 10.12. Прямое и обратное золотые сечения отрезка

Выразим через  и отрезок ab отрезки ас и cb: аc =  ab; cb=  ac = ² ab .

Из условия аc + cb = ab после подстановки данных выражений и сокращения на аb получим следующее квадратное уравнение относительно  :

² +  - 1 = 0 .

Решая его, находим корни:

Отбрасывая отрицательный корень, получим искомую величину отношения:

Разбивать отрезок [a,b] можно не только в прямом, но и в обратном направлении – от b к a. Аналогичная точка d лежит симметрично с относительно средней точки интервала (a+b)/2 (рис.10.12 б).

Величину отношения ad/ab получим, вычитая  из 1:

Точки d, с, задающие обратное и прямое разбиение отрезка в золотом сечении, обладают следующими свойствами.

1. Если отбросить часть отрезка [а,d], то с – золотое сечение оставшейся части [d, b].

2. Если отбросить часть отрезка [с, b], то d – золотое сечение оставшейся части [a, с].

Данные свойства можно доказать непосредственной подстановкой значений

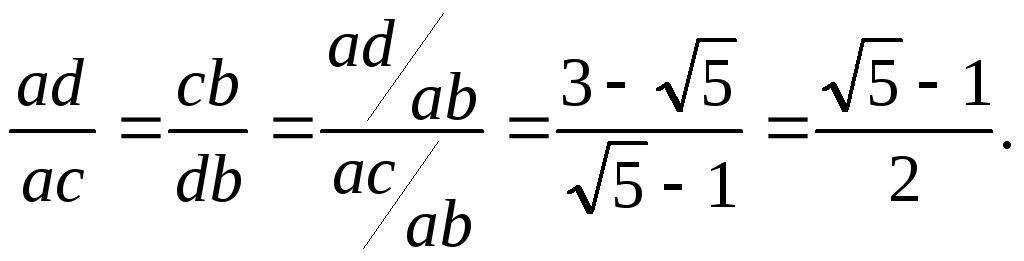
Допустим, необходимо с точностью  найти минимум унимодальной функции F(x) на [a,b].

Предварительные действия (Шаг 0).

Доверительный отрезок принимаем равным заданному: а₀ = а , b₀ = b .

Шаги i (i>0) выполняются в цикле при выполнении условия (b_i - a _i >).

Шаг 1 . 1. Расчет положения двух пробных точек:

х₂ =а₀ + ( b₀ - а₀ ) а₀ + 0,618 ( b₀ - а₀ );

х₁ =( b₀ + а₀ ) - x₂  а₀ + 0,382( b₀ - а₀ ).

2. Расчет значений функций F(x₁) и F(x₂).

3. Анализ значений функции в точках х₁ , х₂ и изменение доверительного отрезка по аналогии с дихотомией:

а) при F(x₁)  F(x₂) принимаем: a₁ = х₁ , х₁ = х₂ , b₁ = b₀ ,

б) при F(x₁) < F(x₂) принимаем: a₁ = а₀ , х₂ = х₁ , b₁ = х₂ .

4. Проверка окончания цикла: если (b₁ - a₁ ) > -продолжение цикла, иначе - выход.

Шаги i (i>1) . Из предыдущей итерации (i-1) известно одно значение функции F(x) во внутренней точке х доверительного отрезка [a_i-1; x _i-1]. Поэтому для сокращения достаточно ввести только одну новую пробную точку.

1. Расчет положения новой пробной точки: х = (b_i-1 + а_i-1) - х, расчет значения функции F(x).

2. Упорядочение пробных точек х, х и значений функции в них:

если (х < х), то { х₁ = х; F(x₁)=F(x); х₂ = х ; F(x₂)=F(x) };

иначе { х₁ = х ; F(x₁)=F(x) ; х₂ = х ; F(x₂)=F(x) }.

Пункты 3 и 4 совпадают с шагом 1.

Скорость сходимости и точность метода. Так как на каждом шаге длина доверительного отрезка сокращается в  = 1/  1,618 раз, то длина [a₁ ,b₁] связана с длиной [a, b] следующим образом: b₁ - a₁ = (b₀ - a₀ ) = (b - a ).

По аналогии для произвольного шага k длина доверительного отрезка: b_k - a_k =  ^k (b - a).

Процесс заканчивается, когда выполняется неравенство b_k - a_k =  ^k(b - a)  .

Отсюда следует, что номер шага k, на котором достигается требуемая точность  , равен k() = ]log_ (b - a)/ [ = ]log_ M [.

На первом шаге выполняется два вычисления целевой функции, на всех последующих n_ш=1. Поэтому полное число необходимых вычислений F(х)

п() =1+ n_ш k() = 1+] log _ ((b - a)/)[ .

Зависимость  (п) находим из равенства (b -a)/ =  ^(n-1):  (п) = (b - a) ^(n-1).

Асимптотические скорости роста зависимостей  (n) и n () для метода золотого сечения:

 (n) = O[(b-a) ⁿ];

п() = O [log _ ((b - a)/)] =O [log _ M].

Данный метод является ещё более быстрым по сравнению с дихотомией, так как в формуле для п() основание логарифма   1,618 < 2. Как и дихотомия, он является регулярным. Также он принадлежит к группе так называемых симметричных методов.

Последовательный метод определения экстремума называют симметричным, если на каждом i–том шаге поиска экстремума на доверительном отрезке [a_i,b_i] уже известна одна пробная точка x₁ и значение целевой функции F(x₁) в ней. Вторая (новая) пробная точка x₂ определяется как симметричная x₁ относительно средней точки (a_i+b_i)/2 доверительного интервала: x₂ = a_i+ b_i - x₁.

Метод дихотомии не является симметричным.

Замечание 1. Известная пробная точка x₁ в симметричном методе может быть как меньше, так и больше значения (a_i+b_i)/2 .

Замечание 2. Свойство симметрии метода позволяет значительно упростить расчёт новых пробных точек. Формула x₂ = a_i+ b_i - x₁ позволяет рассчитать вторую пробную точку x₂ независимо от того, как первая точка x₁ расположена относительно средней точки доверительного отрезка (до или после).

Замечание 3. В практических расчетах при большом числе итераций из-за накопления погрешностей вычисления положение пробной точки x₁ на отрезках [a_i,b_i] может значительно отклоняться от золотого сечения. При этом, соответственно, полное число необходимых вычислений целевой функции п() будет увеличиваться. Для предотвращения этого явления, положение точки x с известным значением функции можно периодически уточнять по формулам х=a+(b-a) либо х=a+(1-)(b-a) в зависимости от того, к какому из данных значений она ближе.

Пример 1. Найти минимум функции F(х) = х² –2х на доверительном отрезке [0,2;2] по методу золотого сечения при заданной точности  =0,5.

Решение.

Шаг 0. а₀ = а , b₀ = b .

Шаг 1. Расчет положения двух пробных точек: х₂=а₀+(b₀–а₀) 1,3124; х₁=(b₀+а₀)-х₂)  0,8876. Значения функции в них: F(x₁) = -0,9874; F(x₂) = -0,7768. Так как F(x₁)<F(x₂), то отбрасываем часть доверительного отрезка [x₂;b₀]. Получаем новый доверительный отрезок [а₁;b₁] = [0,2;1,3124].

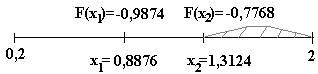
b₁-а₁ = 1,1124 >  = 0,5; продолжаем поиск.

Шаг 2. Границы доверительного отрезка а₁ = 0,2; b₁ = 1,3124 . На нем известно значение функции в точке х 0,8876, F(x) = -0,9874.

Новая пробная точка: х =( b₁+а₁) - 0,8876  0,6248. Значение функции в новой точке х: F(x) = -0,8592.

Поскольку х<х, то принимаем х₁ = х ; F(x₁) = F(x); х₂ = х; F(x₂) = F(x).

Так как F(x₁) > F(x₂), то отбрасываем часть доверительного отрезка [a₁;x₁]. Получаем новый отрезок [а₂;b₂] = [0,6246;1,3124].

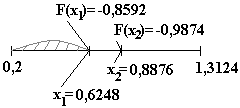
b₂-а₂ = 0,6878 >  = 0,5; продолжаем поиск.

Шаг 3. а₂= 0,6246; b₂= 1,3124 . Известно значение функции в точке х 0,8876, F(x) = -0,9874.

Новая пробная точка: х = (b₂+а₂) - 0,8876  1,0494.. Значение функции в новой точке х: F(x)= --0,9976.

Поскольку х>х, то принимаем х₁= х; F(x₁) = F(x); х₂=х ; F(x₂) = F(x ).

Так как F(x₁)>F(x₂), то отбрасываем часть доверительного отрезка [a₁; x₁] и получаем отрезок [а₃; b₃] = [0,8876; 1,3124].

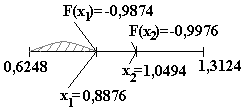
b₃-а₃=0,4248 <  =0,5; следовательно, поиск завершен.

Ответ. Выполнено 3 шага, использовано 4 пробных точки. Найден итоговый доверительный интервал: [а₃ , b₃] = [0,8876; 1,3124] длины 0,4248.

Как видно из Примера 1 п.10.3, число необходимых вычислений функции сократилось по сравнению с методом дихотомии с 6 до 4.

Вопросы для проверки знаний.

1. Что называют а) золотым сечением отрезка, б) прямым и обратным золотым сечением отрезка ?

2. Как практически рассчитать точки, задающие прямое и обратное золотое сечение отрезка ?

3. Какое свойство золотого сечения используется при сокращении доверительного отрезка ?

4. Какие методы называют симметричными и как симметричность используется для упрощения расчета пробных точек ?

5. Как выполняются первый и последующие шаги в методе золотого сечения ?

6. За счет чего метод золотого сечения является более быстрым по сравнению с дихотомией ?

Практические задания.

Решить по методу золотого сечения задачи 1)-13) из п.10.2.