7. Мощность в цепи переменного тока

1. Общие понятия о мощности

Мощность – это количество потребленной энергии в единицу времени.

В ОТЦ рассматриваются следующие виды мощности:

1. мгновенная – мощность, вычисляемая через мгновенные токи и напряжения;

2. активная – мощность в резистивных элементах;

3. реактивная – мощность в реактивных элементах (L и C);

4. полная – совместная мощность в RLC-элементах;

5. комплексная – мощность, вычисляемая через комплексные токи и напряжения.

2. Мощность в резистивном элементе

Зададимся гармоническим током

и рассмотрим мгновенную мощность

- амплитуда мгновенной мощности в R

Этим элементом всегда потребляется энергия. Для оценки потребления изменяющееся мощности используется среднее значение мощности за период. Ему дали название активная мощность (P).

3. Мощность в индуктивном и емкостном элементах (реактивных элементах)

Рассмотрим гармонический ток

Определим мгновенную мощность в индуктивности

Когда p_L(t)> 0. индуктивность запасает энергию, а когда < 0, то возвращает, поэтому ее можно назвать обменной мощностью .

Мощность в индуктивности характеризуют амплитудой мгновенной (обменной) мощности:

- индуктивная мощность, относят к типу реактивной мощности.

Аналогично в емкостном элементе. Емкостной элемент какое-то время потребляет энергию, какое-то время отдает. (Все это справедливо для идеальных элементов).

Здесь рассматривается емкостная мощность Q_C, которая по смыслу является амплитудой мгновенной (обменной) мощности в емкостном элементе. С учетом того, что мгновенная емкостная мощность противоположна по фазе индуктивной, то

Р_C (сред) = 0

Можно определять и общую реактивную мощность: Q=Q_L+ Q_C

Если есть разнотипные элементы, то еще определяется полная мощность S (аналогично полному сопротивлению), поскольку мгновенная реактивная мощность по фазе колебания сдвинута относительно мгновенной активной на четверть периода (90⁰), то:

.

4. Мощность на участке электрической цепи

Для цепи при гармоническом воздействии можно записать

Можно определить мгновенную мощность на участке цепи p(t)=u(t)i(t)

Если использовать свойства тригонометрических функций, то мгновенную мощность можно расписать на мгновенную активную мощность и мгновенную реактивную мощность и выделить постоянную составляющую - среднее значение (активную мощность).

Треугольник мощностей:

Полная мощность – максимально возможная активная мощность (cosφ =1).

5. Комплексная мощность

Поскольку при расчетах с гармоническими токами используются комплексные токи и напряжения, то целесообразно ввести понятие комплексной мощности.- аналогично комплексному сопротивлению. Здесь надо учесть, что φ=ψ_U – ψ_I

,

где символ * - переход к комплексно сопряженному числу.

Рассмотрим мощности источников:

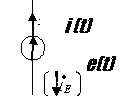p_e(t)= i(t)e(t)=p_a(t)+p_p(t) Это меняющаяся величина.

(если ток противоположен ЕДС, то в формуле мощности берется знак - )

Для комплексной формы

, где

(если ток взят противоположного направления ЭДС, то следует поставить знак - ). Здесь так же выделяют активную (среднюю за период) и реактивную (амплитуду обмена ) мощности источника.

Аналогично для источника тока

p_J(t)=j(t)u_J(t) . Если напряжение источника выбрать не противоположно току то надо в формуле мощности ставить знак - .

В комплексной форме

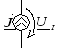
Активная мощность определяет энергию, которую в среднем отдает источник за период, а реактивная определяет .амплитуду обменной мощности источника, которой он обменивается с пассивными элементами цепи при гармоническом воздействии...