§7. Теорема обратимости или взаимности

Справедлива для линейных обратимых цепей: все элементы линейны и обратимы по передаче электрической энергии (движения зарядов) в одну и другую сторону.

Теорема Если некоторый источник ЭДС вызывает в какой-то ветви пассивной обратимой цепи некоторый ток, то будучи перемещен в эту вторую ветвь, он вызовет в первой ветви, где раньше был, точно такой же ток. Справедлива и дуальная теорема.

Доказательство

Применим метод контурных токов, будем выбирать контуры так, чтобы первая ветвь входила только в один первый контур, а вторая – только во второй контур, тогда токи этих ветвей будут равны этим контурным токам.

В первой схеме:

Во второй :

, тогда

Эти два выражения отличаются на и. Если все элементы в цепи обратимы, то . В этом случае и .

Применение теоремы

Теорему целесообразно применять при расчете токов методом наложения, когда надо находить частичные токи от каждого источника в отдельности, рассчитав ток от одного источника напряжения и пропорционально изменяя токи от источников в других ветвях.

Примеры

Применим МЭИН для нахождения тока I5

. Рассмотрим схему для нахождения Uxx

На основе 2 закона Кирхгофа Uxx=I4^׳▪R4+E4. Чтобы найти ток I4^׳ можно применить МКТ. Тогда получим, что I4^׳=I1к и I1к(R1+R3+R4)+J2R1=E1+E3-Е4

Для нахождения Rвх рассмотрим пассивизированную схему (без источников)

Rвх

,

Теорему взаимности целесообразно применять в методе наложения, когда ищутся частичные токи от отдельных источников. Найдя ток от одной ЕДС во всех ветвях можно сразу сказать, что другие ЕДС вызовут в этой ветви токи пропорциональные их отношению.

, тогда

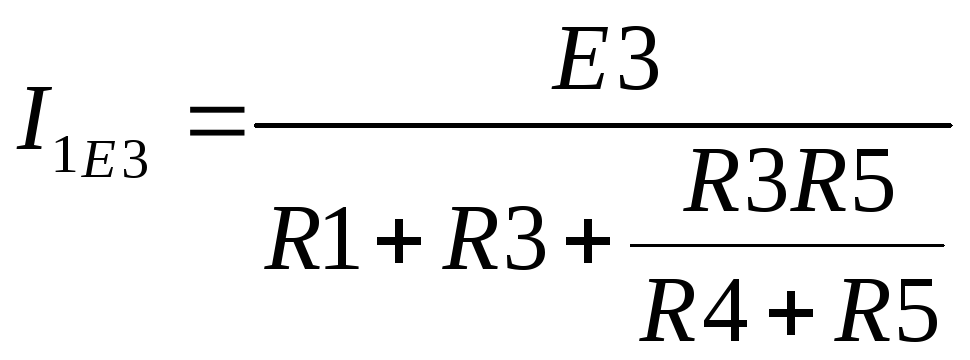
Расчет электрических цепей с управляемыми источниками

Рассмотрим схему с транзистором. З

десь есть разные источники e_C ( источник сигнала - переменный) и U_ПИТ ( источник питания - постоянный), поэтому применяется метод наложения.

Рассмотрим расчет для переменных составляющих, получающихся от действия e_C (t). Для этой схемы можно применять любые методы расчета по составленной расчетной эквивалентной схеме, где транзистор заменен схемой замещения с управляемым источником ИТУТ с выражением I_K=βI б. . На первом этапе управляемый источник считается независимым и составляется система уравнений по какому-то методу (для гармонического воздействия в комплексной форме).

3 узел

1 узел 2 узел

U_3УЗ U_1УЗ U_2УЗ

4 узел (базисный)

U_1УЗ(1/(R_И+Z_C1)+1/R_Б+1/R₁) – U_2УЗ1/R_Б – U_3УЗ1/R₁ = E_C/ (R_И+Z_C1)

- U_1УЗ (1/R_Б) + U_2УЗ(1/R_Б+1/(R_Э+R₂) +1/R_K+1/Z_CK) – U_3УЗ(1/R_K+1/Z_CK) = - I_K

- U_1УЗ (1/R₁) - U_2УЗ(1/R_K+1/Z_CK) + U_3УЗ(1/R₁+1/R₃+1/R_K+1/Z_CK+1/(Z_C2+R_H) = = I_K

На втором этапе вместо тока управляемого источника I_К подставляем его значение. На третьем этапе управляющую величину Iб записываем в зависимости от метода для МКТ через контурные токи, а для МУН через узловые напряжения I б =(U_2УЗ – U _1УЗ) / R_Б.

Далее делаются алгебраические преобразования и решается система уравнений. Токи определяются по соответствующим формулам, например ток нагрузки I_H = U_3УЗ/( Z_C2+R_H) , если направление тока взять вниз.

Усилитель с коэффициентом усиления k. в общем случае, это ИНУН и

у простого усилителя k – коэффициент управления – простое число.

Операционный усилитель, микросхема, и его простейшая схема замещения

μ – коэффициент усиления операционного усилителя