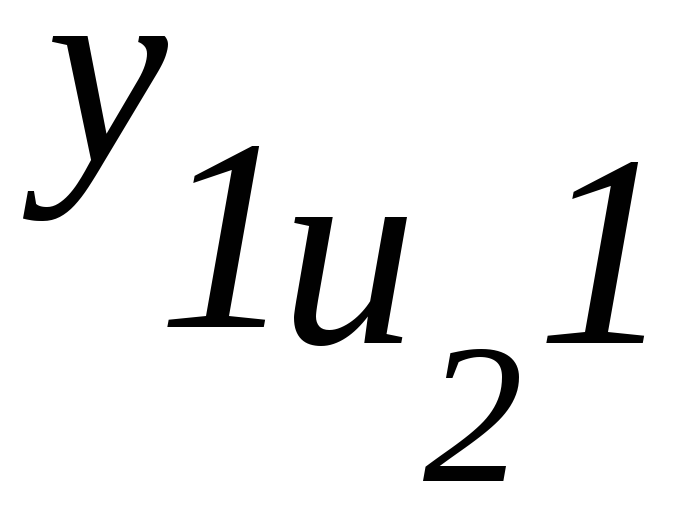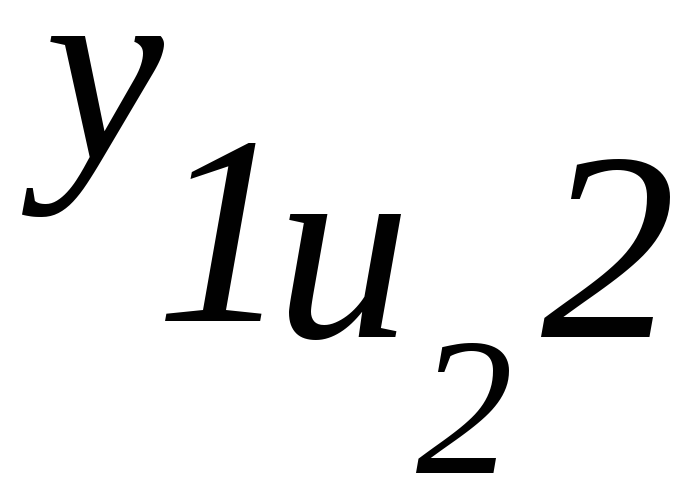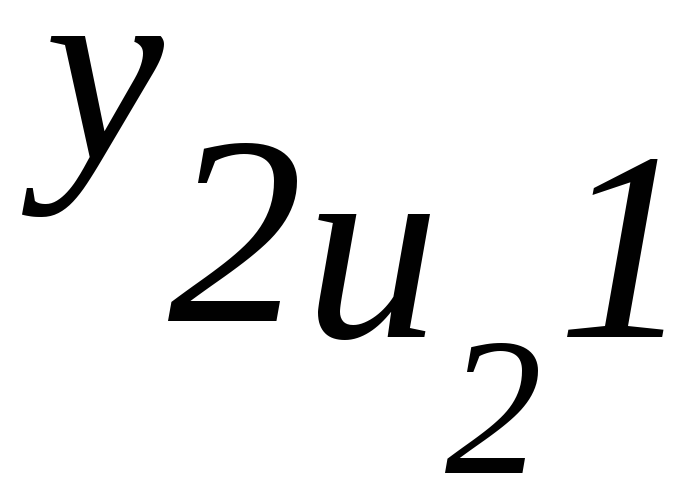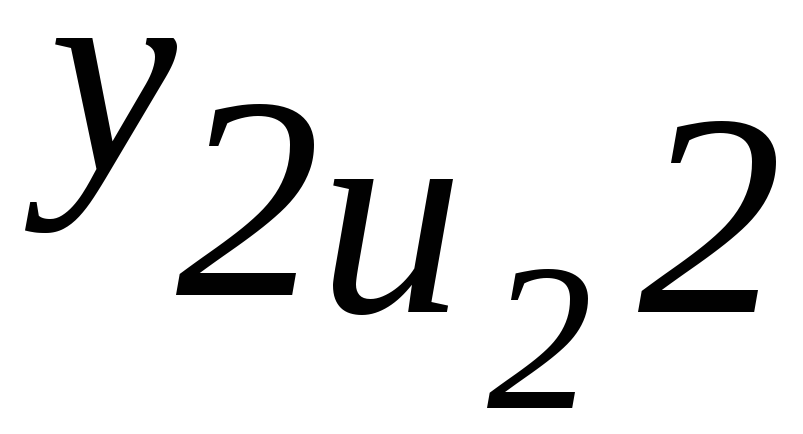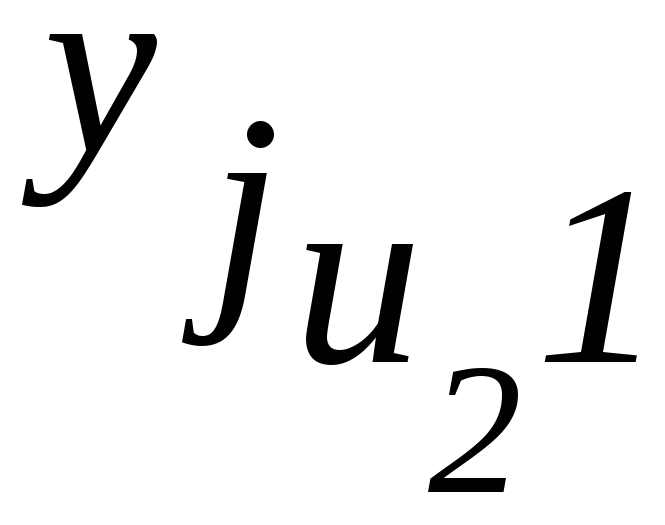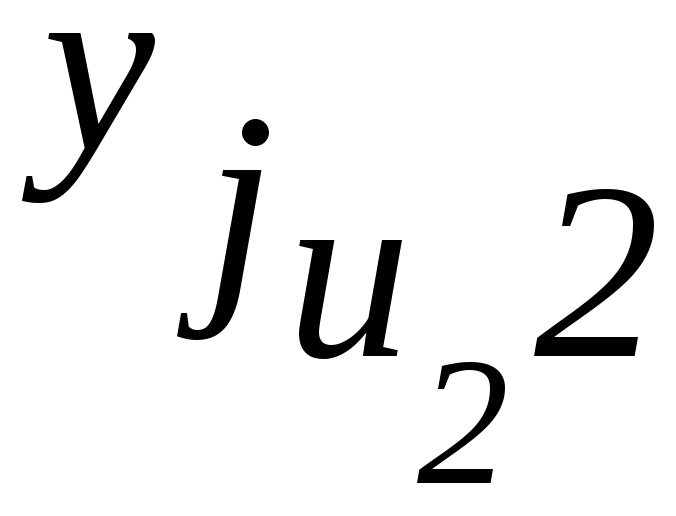- •Основи теорії планування експерименту
- •1 Метод контрольних меж
- •1.1 Теоретичні відомості
- •1.1.1 Загальні відомості
- •1.1.2 Коротка історична довідка
- •1.1.3 Невизначеність при проведенні експерименту
- •1.1.4 Стандартна невизначеність при проведенні експерименту
- •1.1.5 Аналіз результатів повторних спостережень
- •1.1.6 Перевірка гіпотези про вид закону розподілу результатів
- •1.1.7 Методи перевірки гіпотез про вид закону розподілу
- •1.1.7.1 Критерій 2 Пірсона
- •Продовження таблиці 1.2
- •1.1.7.2 Складений критерій
- •1.1.7.3 Обробка результатів кількох серій вимірювань
- •1.1.8 Вимірювання невипадкових величин та їх реалізацій Призначення контрольних меж. Рівноточні виміри постійної величини
- •1.1.9 Статистична характеристика якості продукції
- •1.1.10 Статистичний контроль якості продукції
- •1.1.11 Техніка контрольних карт
- •1.1.12 Форма контрольної карти типу "середнє-розмах"
- •2 Однофакторний дисперсійний аналіз
- •2.1 Теоретичні відомості
- •2.1.1 Постановка задачі
- •2.1.2 Постановка задачі в загальному вигляді
- •Припущення, на яких базується дисперсійний аналіз
- •2.1.4 Ідея дисперсійного аналізу
- •Однофакторний аналіз
- •2.1.6 Розкладання сум квадратів
- •2.1.7 Оцінка дисперсій
- •2.1.8 Оцінка впливу фактора
- •2.1.9 Випадок нерівнокількісних спостережень
- •2.1.10 Розрахункові формули для суми
- •3 Багатофакторний дисперсійний аналіз
- •3.1 Теоретичні відомості
- •3.1.1 Постановка задачі
- •3.1.2 Розкладання сум квадратів
- •3.1.3 Оцінка дисперсій
- •3.1.4. Оцінка впливу факторів
- •3.1.5 Розрахункові формули для сум
- •3.1.6. Опорна стрижнева порцелянова ізоляція
- •4.1 Теоретичні відомості
- •4.2 Багатофакторний експеримент
- •4.2.1 Вибір моделі
- •4.2.2 Повний факторний експеримент
- •4.2.3 Дробовий факторний експеримент
- •4.2.4 Проведення експерименту і обробка його результатів
- •4.2.5 Прийняття рішень
- •4.2.6 Випробування при підвищених і граничних навантаженнях
- •5 Лабораторна робота № 1
- •5.2 Хід роботи
- •5.3 Приклад виконання завдання
- •5.3.1 Завдання
- •5.3.2 Рішення задачі
- •5.4 Варіанти завдань
- •5.5 Контрольні питання
- •6 Лабораторна робота № 2 однофакторний дисперсійний аналіз
- •6.2 Хід роботи
- •6.3 Приклад виконання завдання
- •6.3.1 Завдання
- •6.3.2 Рішення задачі
- •6.4 Варіанти завдань
- •6.5 Контрольні питання
- •7 Лабораторна робота № 3 багатофакторний дисперсійний аналіз
- •7.2 Хід роботи
- •7.3 Приклад виконання завдання
- •7.3.1 Завдання
- •7.3.2 Рішення задачі
- •Двофакторний аналіз
- •7.4 Варіанти завдань
- •7.5 Контрольні питання
- •8 Лабораторна робота № 4
- •8.2 Теоретичні відомості
- •8.3 Хід роботи
- •8.4 Контрольний приклад
- •8.4.1 Домашня підготовка
- •8.4.2 Робота в лабораторії
- •8.5 Формули для розрахунку
- •8.6 Варіанти завдань
- •8.7 Контрольні питання
- •Література
- •Основи теорії планування експерименту
- •21021, М. Вінниця, Хмельницьке шосе, 95 , внту
- •21021, М. Вінниця, Хмельницьке шосе, 95 , внту
2.1.10 Розрахункові формули для суми
Обчислювальний алгоритм однофакторного дисперсійного аналізу спрощується, якщо для розрахунку сум квадратів відхилень використовувати перетворення
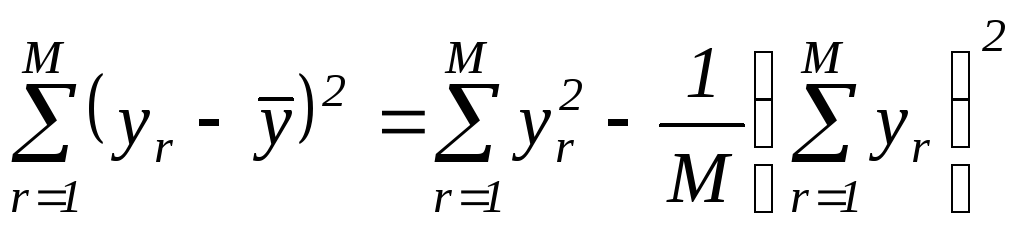 .
(2.37)
.
(2.37)
Тоді для сум отримуємо зручні розрахункові формули:
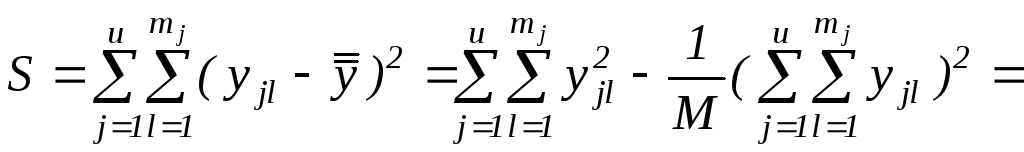
![]() (2.38)
(2.38)
![]()
![]() (2.39)
(2.39)
![]()
![]() .
(2.40)
.
(2.40)
Таким чином, для проведення дисперсійного аналізу достатньо зробити такі попередні обчислення:
1) підсумки спостережень за серіями
![]() (2.41)
(2.41)
2) сума квадратів усіх спостережень
![]() (2.42)
(2.42)
3) сума квадратів підсумків за серіями, поділена на кількість спостережень в серії
![]() (2.43)
(2.43)
4) квадрат загального підсумку, поділений на кількість всіх спостережень
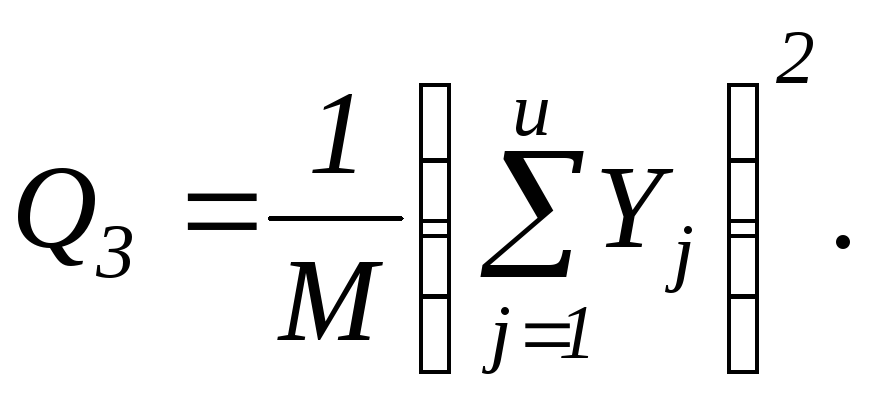 (2.44)
(2.44)
3 Багатофакторний дисперсійний аналіз
3.1 Теоретичні відомості
3.1.1 Постановка задачі
Розглянемо
вплив двох одночасно діючих факторів
x1
і x2
на
результат спостережень
![]() (лабораторна робота 3).
(лабораторна робота 3).
Результати
експерименту наведені в таблиці 3.1 і
містять
![]() спостережень параметра
спостережень параметра
![]()
де
j -
порядковий номер рівня варіювання
фактора
![]()
g
- порядковий номер рівня варіювання
фактора
![]()
l - порядковий номер досліду, який дублюється в серії при кожному jg сполученні рівнів двох факторів,
![]() (для спрощення розрахунків розглянемо
спочатку випадок рівно кількісних
спостережень для всіх можливих сполучень
рівнів, тобто
(для спрощення розрахунків розглянемо
спочатку випадок рівно кількісних
спостережень для всіх можливих сполучень
рівнів, тобто
![]() ).
).
Обчислимо
середні арифметичні
![]() серій з m
повторних
спостережень для кожного сполучення
рівнів j
і g факторів
x1
і x2
серій з m
повторних
спостережень для кожного сполучення
рівнів j
і g факторів
x1
і x2
![]() ;
(3.1)
;
(3.1)
середні
арифметичні
![]() по рядках з
по рядках з
![]() паралельних спостережень для будь-якого
j-го
рівня фактора x1
паралельних спостережень для будь-якого
j-го
рівня фактора x1
![]() (3.2)
(3.2)
середні
арифметичні
![]() по рядках з
по рядках з
![]() паралельних спостережень для будь-якого
g-го
рівня фактора x2
паралельних спостережень для будь-якого
g-го
рівня фактора x2
![]() (3.3)
(3.3)
загальне
середнє арифметичне
![]() всіх
всіх
![]() спостережень за всіма
спостережень за всіма
![]() сполученнями рівнів
сполученнями рівнів
![]() (3.4)
(3.4)
При
вказаному розташуванні спостережень
їхнє розсіювання в кож-ній серії щодо
середнього тієї ж серії, обумовлене
дією тільки випадкових причин (з
дисперсією ).
Розсіювання ж самих середніх серій за
всіма можливими
сполученнями рівнів x1
і x2
навколо загального середнього крім
фактора випадковості викликано впливом
фактора взаємодії x1x2
(з дисперсією
![]() ).
Крім цих
факторів на розсіювання середніх по
рядках впливає тільки один фактор x1
(з дисперсією
).
Крім цих
факторів на розсіювання середніх по
рядках впливає тільки один фактор x1
(з дисперсією
![]() ),
а на
розсіювання середніх по стовпцях -
тільки один фактор x2
(з дисперсією
),
а на
розсіювання середніх по стовпцях -
тільки один фактор x2
(з дисперсією
![]() ),
тому що всі рівні іншого фактора в
кожному з цих випадків усереднені.
),
тому що всі рівні іншого фактора в
кожному з цих випадків усереднені.
Таблиця 3.1 - Результати експерименту
|
фактора x2
№ j рівня фактора x1 |
1 |
2 |
... |
g |
... |
u2 |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
y111 |
Y121 |
… |
y1g1 |
… |
|
|
|
y112 |
Y122 |
… |
y1g2 |
… |
|
||
|
… |
… |
… |
… |
… |
… |
||
|
y11l |
Y12l |
… |
y1gl |
… |
|
||
|
… |
… |
… |
… |
… |
… |
||
|
y11m |
y12m |
… |
y1gm |
… |
|
||
|
2 |
y211 |
Y221 |
… |
y2g1 |
… |
|
|
|
y212 |
Y222 |
… |
y2g2 |
… |
|
||
|
… |
… |
… |
… |
… |
… |
||
|
y21l |
Y22l |
… |
y2gl |
… |
|
||
|
… |
… |
… |
… |
… |
… |
||
|
y21m |
y22m |
… |
y2gm |
… |
|
||
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|
j |
yj11 |
yj21 |
… |
yjg1 |
… |
|
|
|
yj12 |
yj22 |
… |
yjg2 |
… |
|
||
|
… |
… |
… |
… |
… |
… |
Продовження таблиці 3.1
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|||||||
|
|
yj1l |
yj2l |
… |
yjgm |
… |
|
|
|||||||
|
… |
… |
… |
… |
… |
… |
|||||||||
|
yj1m |
yj2m |
… |
yjgm |
… |
|
|||||||||
|
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
. . . |
|||||||
|
u1 |
|
|
… |
|
… |
|
|
|||||||
|
|
|
… |
|
… |
|
|||||||||
|
… |
… |
… |
… |
… |
… |
|||||||||
|
|
|
… |
|
… |
|
|||||||||
|
… |
… |
… |
… |
… |
… |
|||||||||
|
|
|
… |
|
… |
|
|||||||||
|
|
|
|
… |
|
… |
|
|
|||||||

 №
g
рівня
№
g
рівня