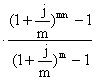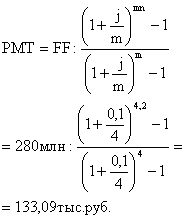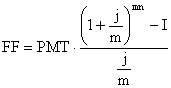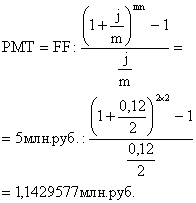- •Конспект лекций Теория статистики. Оглавление
- •Тема 24. Статистика рыночной конъюнктуры 222 Тема 1. Предмет, метод и организация статистики
- •Тема 2. Статистическое наблюдение
- •2.1. Основные формы, виды и способы статистического наблюдения
- •2.2. Программно - методологические вопросы статистического наблюдения
- •2.3. Основные организационные вопросы статистического наблюдения
- •2.4. Точность и контроль статистического наблюдения
- •Тема 3. Статистическая сводка и группировка
- •3.1.Задачи сводки и ее содержание
- •3.2. Виды статистических группировок
- •3.3. Принципы построения статистических группировок и классификаций
- •3.4. Сравнимость статистических группировок. Вторичная группировка
- •3.5. Статистическая таблица и ее элементы
- •Тема 4. Абсолютные и относительные статистические показатели
- •4.1. Классификация статистических показателей
- •4.2. Абсолютные показатели
- •4.3. Относительные показатели
- •Тема 5. Графическое изображение статистических данных
- •5.1. Понятие о статистическом графике. Элементы статистического графика
- •5.2. Классификация видов графиков
- •877,5 Тонн 290 млн. Руб.
- •0 1 2 3 4 5 6 7 8 9 10 Стоимость основных
- •Тема 6. Средние показатели
- •6.1.Сущность средних показателей
- •6.2. Средняя арифметическая величина и ее свойства
- •6.3. Другие виды средних величин
- •6.4. Структурные средние
- •Тема 7. Анализ вариации
- •7.1. Основные показатели вариации
- •7.2. Использование показателей вариации в анализе взаимосвязей
- •Тема 8. Выборочное наблюдение
- •8.1. Выборочное наблюдение как важнейший источник статистической информации
- •8.2. Основные способы формирования выборочной совокупности
- •8.3. Определение необходимого объема выборки
- •8.4.Оценка результатов выборочного наблюдения и распространение их на генеральную совокупность
- •8.5. Малая выборка
- •Тема 9. Статистическое изучение взаимосвязи социально-экономических явлений
- •9.1. Причинность, регрессия, корреляция
- •9.2.Парная регрессия на основе метода наименьших квадратов и метода группировок
- •9.3. Множественная (многофакторная) регрессия
- •9.4. Собственно-корреляционные параметрические методы изучения связи
- •9.5. Принятие решений на основе уравнений регрессии
- •9.6. Методы изучения связи качественных признаков
- •9.7. Ранговые коэффициенты связи
- •Тема 10. Статистическое изучение динамики социально-экономических явлений
- •10.1.Понятие и классификации рядов динамики
- •10.2.Сопоставимость уровней и смыкание рядов динамики
- •10.3.Показатели изменения уровней ряда динамики
- •10.4. Методы анализа основной тенденции (тренда) в рядах динамики
- •10.5. Методы выявления сезонной компоненты
- •10.6. Элементы прогнозирования и интерполяции
- •Тема 11. Статистический анализ структуры
- •11.1 Понятие структуры и основные направления ее исследования
- •11.2. Частные показатели структурных сдвигов
- •11.3. Обобщающие показатели структурных сдвигов
- •11.4. Показатели концентрации и централизации
- •Тема 12. Индексы
- •12.1. Общие понятия об индексах
- •12.2. Агрегатные индексы
- •12.3. Сводные индексы в средней арифметической и средней гармонической формах
- •12.4. Системы индексов
- •12.5. Индексы постоянного и переменного состава
- •Тема 13. Система статистических показателей отраслей и секторов экономики, основные группировки и классификации в статистике
- •Тема 14. Статистика населения. Статистика численности, состава и миграции населения
- •14.2. Статистика естественного движения и миграции населения
- •Тема 15. Статистика рынка труда, использования рабочего времени, производительности и оплаты труда
- •15.1. Статистика экономической активности населения
- •15.2 Статистика использования рабочего времени
- •15.3 Статистика производительности труда
- •15.4 Статистика оплаты труда
- •Тема 16. Статистика национального богатства
- •16.1 Статистика основных фондов и оборудования
- •Наличие, движение, структура основных средств за 200б год.
- •16.2 Статистика оборотных фондов
- •Тема 17. Статистика рынка товаров и услуг
- •17.1 Статистика товаров
- •17.2 Статистика услуг.
- •Тема 18. Статистика издержек производства и обращения. Статистика финансовых результатов деятельности предприятий
- •18.1 Статистика издержек производства и обращения
- •18.2 Статистика финансовых результатов деятельности предприятий
- •Тема 19. Статистика уровня жизни населения
- •Тема 20. Статистика финансов
- •Тема 21.Система снс и макроэкономические показатели производства товаров и услуг.
- •Тема 22. Статистика качества
- •Тема 23. Статистика научно-технического прогресса
- •1. Понятие и направление научно-технического прогресса
- •2. Современная статистика нтп – статистика инновационной деятельности
- •3. Статистическое изучение процессов создания и передачи технологий
- •4. Статистическая оценка научного потенциала
- •5. Обобщающие показатели инновационной деятельности
- •6. Частные показатели эффективности внедрения новой техники и новых технологий
- •Тема 24. Статистика рыночной конъюнктуры
Тема 20. Статистика финансов
Денежный агрегат МО определяется как сумма наличных денег в обращении. Денежный агрегат МО в совокупности с остатками на расчетных, текущих счетах в банках, на депозитных вкладах во всех кредитных учреждениях, являющимися безналичной денежной массой, составляет агрегат М2.
Количество оборотов (V обр) денежной массы за период рассчитывается как отношение объема внутреннего продукта к агрегату М2. Величина, обратная рассчитанной и умноженная на число календарных дней в году покажет скорость обращения совокупной денежной массы:
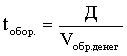
Денежный мультипликатор представляет собой отношение денежной массы (М2) к денежной базе.
Налоговые доходы государственного бюджета включают в себя: налог на прибыль, подоходный налог с физических лиц, налог на добавленную стоимость, акцизы, платежи за использование природных ресурсов, прочие доходы.
Неналоговые доходы составляют: доходы от внешнеэкономической деятельности, доходы от принадлежащего государству имущества, доходы от реализации государственных финансов, прочие доходы.
Текущие расходы складываются из закупок товаров и услуг, выплаты процентов, субсидий и текущих трансфертов. Текущие расходы обеспечивают текущее финансирование органов государственной власти и местного самоуправления, а также бюджетных учреждений.
Капитальные расходы - это вложения в основные фонды, создание государственных запасов и резервов и капитальные трансферты. Капитальные расходы обеспечивают инновационную и инвестиционную деятельность.
Дефицит (профицит) бюджета - превышение расходов (доходов) над доходами (расходами).
Для оценки уровня инфляции вычисляют индекс потребительских цен фиксированного состава Ласпейреса. В зависимости от исходных данных исчисляют агрегатный или средневзвешенный индекс.
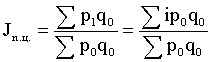
Уровень инфляции оценивают так:
![]()
Для оценки динамики инфляции применяют показатель:
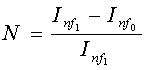
Агрегированный индекс инфляции вычисляется как средневзвешенный индекс из индекса потребительских цен, индексов цен производителей промышленной продукции, индексов цен в капитальном строительстве, индексов цен и тарифов на грузовые перевозки, индексов цен в промышленности на приобретенные ресурсы. Веса для средневзвешенного индекса получают на основе исчисления парных коэффициентов корреляции:
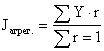
Веса соответственно равны: 0, 203, 0, 221, 0, 193, 0, 174 и 0, 209.
Для исчисления реальной стоимости денег (наращенной с учетом обесценения денег под влиянием инфляции) все формулы корректируются путем деления на
![]() :
:
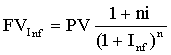 при начислении простых процентов
при начислении простых процентов
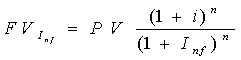 при начислении сложных
процентов,
при начислении сложных
процентов,
где i- ставка процентов за период
n- число процентных периодов
Inf- уровень инфляции за период
PV- первоначальная сумма денег
FV- наращенная сумма денег
К активным статьям баланса банка согласно методологии международной финансовой статистики относятся: резервы, иностранные активы, требования к расширенному правительству, к нефинансовым государственным предприятиям, к предприятиям частного сектора, населению и прочие. К пассивным статьям относятся: депозиты до востребования, срочные и сберегательные депозиты, инструменты денежного рынка, иностранные пассивы, депозиты расширенного правительства, кредиты, предоставленные денежными властями и счета капитала. Сальдо – это разница между итогом актива и пассива баланса, а валюта баланса - их сумма.
При исчислении медианного срока вклада в качестве весов принимаются накопленные частости.
Индекс биржевой активности Доу-Джонса является среднеарифметической невзвешенной величиной из стоимости акций на момент закрытия биржи. В знаменателе вместо числа определяемых признаков используют коэффициент для устранения последствий деления компаний и, соответственно, капитала на одну акцию.
Балансовая таблица счета операций с капиталом и финансовыми инструментами платежного баланса должна иметь вид:
|
|
Дебет |
Кредит |
Сальдо |
|
Счет операций с капиталом Капитальные трансферты Финансовый счет Сектор госуправления Банковский сектор Прочие сектора Итого счет операций с капиталом и финансовыми инструментами |
|
|
|
Решая примеры раздела следует помнить, что суть всех необходимых расчетов заключается в определении стоимости денег в заданный момент времени путем анализа процесса наращения капитала в течение некоторого периода времени. Основной причиной изменения стоимости денег во времени является процент - доход, уплачиваемый за предоставление их в долг. Причем, в финансово-экономических расчетах процент трактуется шире, как показатель доходности даже только предполагаемого изменения капиталов (т.е. реального движения денег может и не быть).
Свое количественное выражение процент находит в:
а) абсолютном показатели доходности - сумме процентных денег, выплаченных за единицу времени (обозначим I);
б) относительном показатели доходности - процентной ставке, равной отношению суммы абсолютного дохода за период времени к размеру капитала.
Методы финансово-экономических расчетов различны в зависимости от вида применяемых процентов. Они подразделяются по способу начисления на:
1) обычные (декурсивные). Эти проценты начисляются в конце периода относительно исходной величины денег. Доход на процент выплачивается в конце процентных периодов финансовой операции;
2) авансовые (антисипативные). Они начисляются в начале периода относительно конечной суммы денег.
Рассмотренным двум видам процентов на практике соответствуют определенные процентные ставки: обычная ставка (ставка процентов (i)) и антисипативная ставка (учетная, дисконтная, вексельная - d ).
Основное отличие процентных ставок: они применяются к различным суммам денег: i -к текущей (исходной, современной) стоимости денег (PV) , ставка d -к будущей стоимости денег (FV).
В зависимости от того, переменная или постоянная величина является базой для начисления процентов, они делятся на:
- простые, которые весь срок обязательства начисляются на первоначальную сумму;
- сложные, база для начисления которых постоянно меняется за счет ранее присоединенных процентов.
Большинство задач финансовой математики связано с исчислением наращенной суммы (как результата операции наращения), современной стоимости денег (как результата дисконтирования), определения ставок доходности помещения капитала, фактора инфляции.
В таблице 20.1 сведены формулы для решения задач при начислении простых процентов.
Таблица 20.1
|
Вид % ставки |
Наращение |
Дисконтирование |
|
i |
|
|
|
d |
|
|
Формулы 1,2,3,4 для определения результатов наращения и дисконтирования по простой ставке процентов используются в расчетах при предоставлении ссуд под простые проценты, по вкладам до востребования, по процентным ценным бумагам.
В формулах 1 и 3 - n - это число процентных периодов, i - ставка за период
ПРИМЕР 1. Сбербанк выдал ссуду 10 млн.руб. на 2 года под 10 простых процентов (годовых). Определить подлежащую возврату сумму, если проценты начисляют в конце года.
|
FV = ? PV =10 млн.руб n= 2 года i = 10% годовых |
FV = РV ( 1 +ni ) = 10 ( 1+ 2 х 0,1) = 12 млн.руб. |
В
формулах 2, 4 аналитически выражен принцип
расчета для случаев, когда срок финансовой
операции и ставка характеризуются
различными промежутками времени (как
правило, ставка - годовая -i , срок операции
- дни, реже - месяцы, кварталы, полугодия
- (t )). В этих формулах срок
финансовой операции и база приведены
в соответствие друг с другом (![]() -срок
приведен в соответствие со ставкой: где
Y - продолжительность
года, выраженная в тех же единицах, что
и t ). Приведение ставки в соответствие
со сроком (
-срок
приведен в соответствие со ставкой: где
Y - продолжительность
года, выраженная в тех же единицах, что
и t ). Приведение ставки в соответствие
со сроком (![]() ) дает такую же формулу.
) дает такую же формулу.
ПРИМЕР 2. Организации предоставлена ссуда 1 млн.руб. под 20%годовых с 1 января по 1 апреля т.г. Определить подлежащую возврату сумму, применить коммерческие проценты с точным числом дней ссуды.
|
FV = ? РV = 1 млн.руб. t(дней) = 31 + 28 + 31 = 90 дней i годовых = 20 % Y = 360 дней
|
|
Естественно, такой же результат дает расчет по принятой операционной практикой формуле:
FV = PV+ %
где %
=
![]()
ПРИМЕР 3. Ставка размещения краткосрочных денежных ресурсов для банков на 3 суток составляет 14% (годовых). Какой объем средств был размещен, если в результате операции поступило 1,5 млн.руб.
|
РV = ? FV =1,5 млн.руб. . i годовых = 14% tсуток = 3 Y=365 дней |
|
По формуле 5 и 6 решаются задачи, связанные с дисконтными ценными бумагами.
ПРИМЕР 4. Учесть дисконтный вексель номинальной стоимостью 10 тысруб. за два месяца до погашения по вексельной ставке 8% годовых.
|
PV = ? FV = 10 тысруб. d годовых = 8 % t = 2 мес. = Y = 12 мес.
|
PV = FV - D (дисконт)
= 10тыс – 10 тыс х
|
ПРИМЕР 5. Дата погашения векселя 5 июня т.г. Какова была его выкупная цена на 23 февраля т.г., если номинал - 1 тысруб., вексельная ставка - 9,5% годовых.
|
FV = 1 тысруб. d год. = 9,5% t = 101 день Y = 360 дней =. |
РV =
1 млн (1- |
Расчеты по формулам сложных процентов проводятся в случае финансовых операций с применяемой сложной процентной ставкой.
В таблице приведены такие формулы для определения наращенной стоимости денег для ставки процентов (i).
|
Вид % ставки |
Наращенная сумма |
|
i |
|
Формулой (7) следует пользоваться, если процентная ставка, срок финансовой операции и период начисления процентов характеризуются одним и тем же промежутком времени. В этом случае: i - процентная ставка за период; n - срок финансовой операции (и число процентных периодов, т.к. проценты начисляются по истечении каждого процентного периода).
ПРИМЕР 6. Ссуда 2 млн.руб. выдана под сложные проценты на 3 года. Процент (10%) начисляется ежегодно в конце периода и присоединяется к основной сумме долга. Определить сумму задолженности к концу финансовой операции.
|
FV = ? PV = 2 млн.руб. t годовых= 10% = n =3 года |
|
Рассмотрим область применения формулы 8. Если проценты начисляются не по истечении периода соответственно заданной процентной ставки (допустим годовой), а чаще - m раз-, то говорят, что имеет место m - кратное начисление процентов. В таком случае годовая базовая ставка по договору (j) не дает полной характеристики доходности финансовой операции. Поэтому годовую базовую ставку будем называть номинальной в отличие от реальной, эффективной ставки (i), которая характеризует полный доход с учетом капитализации.
Формула перехода от номинальной ставки к эффективной
![]()
ПРИМЕР 7. Банк А начисляет проценты один раз в год исходя из 12% годовых., а банк Б - 2 раза в год исходя из 10%годовых. Сравнить доходности операций.
|
А : j = i = 12% m = 1 Б: j = 10% m = 2 |
iБ
= (1 +
iб > iа |
Так же рассчитывают эффективную доходность ценных бумаг при начислении дивидендов чаще, чем один раз в год.
Таким образом, формула 8 используется в случае, когда процентная ставка и срок финансовой операции характеризуются одним и тем же промежутком времени, а период начисления процентов - нет (т.е., допустим, ставка годовая, срок - в годах, а начисляются проценты чаще, несколько раз в год).
ПРИМЕР 8. Пусть во вклад с капитализацией процентов помещен один млн. руб. Исчислить наращенную через 2 года сумму вклада, если проценты начисляют ежеквартально исходя из 24% годовых.
|
FV= ? РV = 1 млн.руб. n = 2 года j годовых = 24% m = 4 (т.е, 4 раза в году ежеквартально начисляют проценты) |
FV
=PV( 1 +
|
Формулой 9 пользуются, если и срок финансовой операции и период начисления, и процентная ставка характеризуются различными промежутками времени (например, ставка - годовая, срок - дни, проценты начисляются ежемесячно).
ПРИМЕР 9. По дебетовой магнитной карте ежеквартально начисляются, присоединяются проценты исходя из 9% годовых. Определить, какой суммой будет располагать владелец карточки через 7 месяцев, если она оформлена на 500USD.
|
FV=? РV
= 500USD
j годовых = 9% t =7 мес. Y = 12 мес. m= 4 |
FV
= PV(1 +
= 500(1 +
|
Если проценты начисляются только за полный процентный период, то 1/3 из степени следует отбросить и возводить во 2-ую степень (т.е. за 7 месяцев минуло 2 полных процентных периода). Бывают случаи, когда за дробную часть процентного периода также начисляются проценты тем или иным способом.
Далее рассмотрим принципы решения задач, связанных с потоками постоянных регулярных финансовых платежей postnumerando.(аннуитетов postnumerando).
Введем обозначение параметров аннуитетов postnumerando:
1) R - размер годового платежа;
2)
![]() =
PMT - размер разового платежа;
=
PMT - размер разового платежа;
3) р - число раз в году поступления разовых платежей ;
4) n - срок финансовой операции;
5) i(j) - процентная ставка кредитных учреждений;
6) m - число раз в году начисления процентов в кредитном учреждении.
Задачи исчисления наращенной стоимости регулярных потоков платежей встречаются, когда надо найти или сумму выплат по ценным бумагам на момент их окончания, или общую сумму задолженности, если средства получали равномерно, частями, или накопленный на момент оценки денежный резерв.
Формулы для исчисления наращенной стоимости (FF) регулярных финансовых потоков postnumerando при условии постоянной ставки процентов выглядят так в зависимости от сочетания параметров m и р.:
1 случай
|
m= 1 р = 1 |
FF = PMT
|
ПРИМЕР 10. Ежегодно в конце периода в течение 3-х лет перечисляли на счет в банк под 20% годовых 100 тысяч рублей (начисление процентов I раз в конце года). Определить накопленную сумму.
|
FF = ? m = 1 p = 1 PMT = 100 тысруб. i годовых = 20 % n = 3 года |
FF=
100тыс |
2 случай
|
m≠1 m≠1 p=1 |
FF=PMT |
ПРИМЕР 11. Определить, по сколько надо вносить на счет под 10 процентов годовых с начислением их ежеквартально, чтобы через 2,5 года собрать 725 тыс руб. Взносы осуществляются один раз в конце года.
|
PMT = ? p = 1 m = 4 n = 2 года FF = 280 тыс руб. j годовых = 10%
|
|
3 случай.
|
m = p = 1 |
|
ПРИМЕР 12. Исчислить размер взноса в конце полугодия для создания через 2 года фонда объемом 5 млн. рублей. Фонд создается в кредитном учреждении, начисляющем проценты каждое полугодие по ставке 12 процентов в год.
|
р = 2 n= 2 FF = 5 млн.руб. j годовых =12% m = 2
|
|

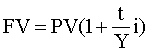 (2)
(2)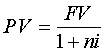 (3)
(3)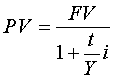 (4)
(4)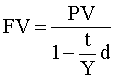 (5)
(5)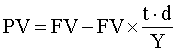 (6)
(6)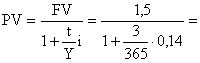 1,498276
млн.руб
1,498276
млн.руб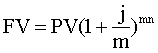 (8)
(8)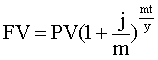 (9)
(9)