7.2. Использование показателей вариации в анализе взаимосвязей
Показатели вариации могут быть использованы не только в анализе колеблемости или изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями.
При проведении такого анализа исходная совокупность должна представлять собой множество единиц, каждая из которых характеризуется двумя признаками - факторным и результативным. Факторным называется признак, оказывающий влияние на взаимосвязанный с ним признак. В свою очередь, этот второй признак, подверженный влиянию, называется результативным.
Для выявления взаимосвязи исходная совокупность делится на две или более групп по факторному признаку. Выводы о степени взаимосвязи базируются на анализе вариации результативного признака. При этом применяется правило сложения дисперсий:
(7.8.)
где
- общая дисперсия;
- средняя из внутригрупповых дисперсий;
- межгрупповая дисперсия.
Межгрупповая дисперсия отражает ту часть вариации результативного признака, которая обусловлена воздействием признака факторного. Это воздействие проявляется в отклонении групповых средних от общей средней:
(7.9.)
где
- среднее значение результативного
признака по i-ой группе;
- общая средняя по совокупности в целом;
- объем (численность) i-ой
группы.
Если факторный признак, по которому производилась группировка, не оказывает никакого влияния не признак результативный, то групповые средние будут равны между собой и совпадут с общей средней. В этом случае межгрупповая дисперсия будет равна нулю.
Средняя из внутригрупповых дисперсий отражает ту часть вариации результативного признака, которая обусловлена действием всех прочих неучтенных факторов, кроме фактора, по которому осуществлялась группировка:
(7.10.)
где
- дисперсия результативного признака
в i-ой группе;
- объем (численность) i-ой
группы.
Теснота связи между факторным и результативным признаком оценивается на основе эмпирического корреляционного отношения:
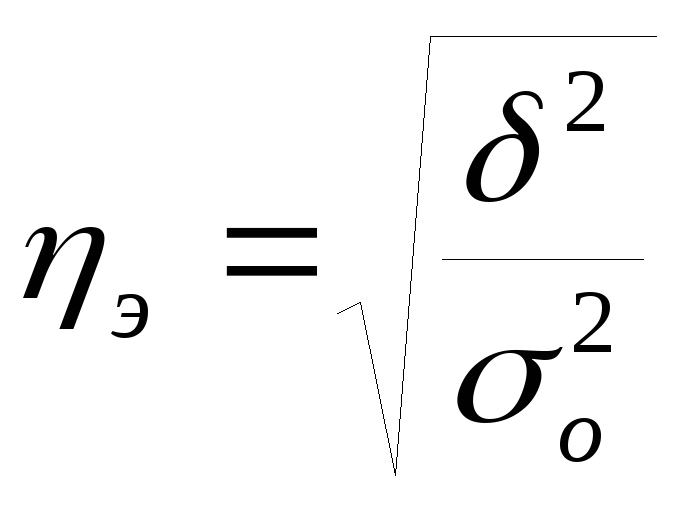(7.11.)
Данный показатель может принимать значение от 0 до 1. Чем ближе к 1 будет его величина, тем сильнее взаимосвязь между рассматриваемыми признаками.
На следующем условном примере исследуем зависимость между собственными и привлеченными средствами коммерческих банков региона:
Таблица 7.2.
-
Банк
Собственные средства, млн. руб.
Привлеченные средства, млн. руб.
1.
70
300
2.
90
400
3.
140
530
4.
110
470
5.
75
255
6.
150
650
7.
90
320
8.
60
240
9.
95
335
10.
115
405
Если взаимосвязь между рассматриваемыми показателями существует, то она обусловлена влиянием объема собственных средств на объем привлеченных средств. Поэтому объем собственных средств выступает в данном примере в качестве факторного признака (X), а объем привлеченных средств в качестве результативного признака (Y).
Произведем группировку банков, выделив две группы по величине собственных средств, например, группу "да 100 млн. руб." и группу "100 млн. руб. и более". Результаты такой группировки представлены в следующей таблице:
Таблица 7.3.
-
№ группы
Собственные средства, млн. руб.
Привлеченные средства, млн. руб.
1.
до 100
300 400 255 320 240 355
2.
100 и более
530 470 650 405
Расчет эмпирического корреляционного отношения включает несколько этапов:
рассчитываем групповые средние:
где i – номер группы;
j – номер единицы в группе.
млн.
руб.;
млн.
руб.
В данном примере при расчете групповых средних мы использовали невзвешенные формулы. Однако, при повторении вариантов для расчета необходимо использовать средние взвешенные.
рассчитываем общую среднюю:
млн. руб.
Данную среднюю также можно было получить как соотношение суммы всех единиц исходной совокупности (без учета деления на группы) к объему всей совокупности, т.е. к общему числу единиц.
рассчитываем внутригрупповые дисперсии:
Если бы варианты имели веса, то для расчета внутригрупповых дисперсий также требовались бы взвешенные формулы.
вычисляем среднюю из внутригрупповых дисперсий:
определяем межгрупповую дисперсию:
находим общую дисперсию по правилу сложения:
На этом этапе возможна проверка правильности выполненных ранее расчетов. Если возвратиться к исходной совокупности и не раздета ее на группы рассчитать дисперсию признака «у», то она должна совпасть с общей дисперсией, полученной по правилу сложения.
Рассчитаем эмпирическое корреляционное отношение:
Полученная величина свидетельствует о том, что фактор, положенный в основание группировки (собственные средства), существенно влияет на размер привлеченных банками средств.