21.1. Спектр собственных значений разностного оператора второй производной.

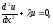
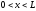
Известно, что дифференциальная задача на собственные значения 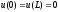(1) имеет бесконечный спектр собственных значений и соответствующих им собственных функций , , .

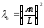Рассмотрим разностный аналог данной задачи на равномерной сетке.

, (2)

, , , .

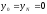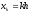Система разностных уравнений (2) представляет собой систему ЛАУ 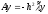с трехдиагональной симметричной квадратной матрицей

.

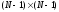
Матрица 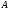имеет диагональное преобладание и у нее имеется 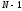собственных значений. Данная матрица может рассматриваться как разностный аналог дифференциального оператора второй производной.

Разностное уравнение (2) можно представить в эквивалентном виде

. (3)

Это разностное однородное уравнение второго порядка, общее решение которого может быть выражено в виде комбинации линейно независимых частных решений.

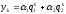(4), где 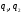- корни характеристического многочлена

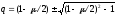. (5)

Решение (4) удовлетворяет нулевым краевым условиям при выполнении равенств

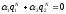, . (6)

Однородная система (6) имеет нетривиальное решение при условии 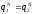. Учитывая, что для корней характеристического уравнения (5) (это доказывается прямыми вычислениями) , имеем

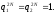
Следовательно, собственные функции, которые для однородного уравнения определяются с точностью до постоянного множителя , имеют вид

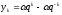, где , .

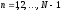Полагая и используя формулу Эйлера, окончательно получаем вид собственных функций разностной задачи

.

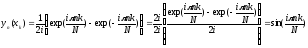Заметим, что характер-е уравнение имеет пару комплексно сопряженных решений (5), причем относительно действительной части этих корней имеем .

Отсюда находим собственные значения, соответствующие полученным собственным функциям:

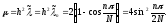
Окончательно приходим к следующему набору собственных функций и собственных значений дискретной задачи:

, , .

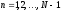Заметим примечательный факт, что набор собственных функций дискретной задачи совпадает в узлах сетки с соответствующими собственными функциями дифференциальной задачи при .

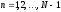Отметим основные отличия собственных значений дискретной задачи от собственных значений дифференциальной задачи.

1. Спектр собственных значений дискретной задачи при любом конечном числе узлов сетки ограничен, и максимальное собственное значение зависит от шага сетки :

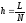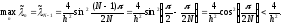
Для сравнения, спектр дифференциальной задачи неограничен: .

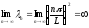2. Для любого фиксированного собственные значения дискретной задачи сходятся к соответствующим собственным значениям дифференциальной задачи при :.

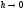Несложно заметить также, что собственные значения дискретной задачи при любом конечном значении шага сетки меньше соответствующих собственных значений дифференциальной задачи. Это непосредственно следует из неравенства при любом 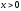. 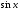Структура собственных значений дискретной задачи позволяет заметить также, что все собственные значения, как и в случае дифференциальной задачи, положительны, различны и возрастают с ростом (последнее следует из свойства монотонного возрастания функции на интервале ).
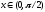