57.БилетЛогарифмическое дифференцирование.

Определение. Логарифмической производной функции y=f(x) называется производная ее логарифма. тогда производная функции y=f(x) может быть найдена так: . Рассмотрим степенную функцию Имеем тем самым формула доказана. Применив прием логарифмического дифференцирования, мы можем вычислить производную показательно-степенной функции . Имеем, функции u(x) v(x) дифференцируемыми в т. x, а функцию u(x)>0 в некоторой окрестности т.x: .

Правило логарифмического дифференцирования рекомендуется применять на практике при дифференцировании произведения многих сомножителей. Дифференцирование неявной функции. Рассмотрим уравнение F(x,y)=0 относительно y. При некоторых условиях это уравнение определяет единственную функцию называемая неявной функцией, задаваемая исходной функцией. Тогда . при дифференцировании применим теорему о производной сложной функции. В результате получиться линейное уравнение относительно y’ уравнение, решая которое находим y’.

Примечания.1) Если производные и удовлетворяют всем условиям доказанной теоремы, то правило Лопиталя-Бернули может быть повторено.

2) Правило Лопиталя остается оправданным если .

3) Предел отношения функции может $ и без того, чтобы $ предел относительно их производных.

4) Правило Лопиталя-Бернули остается в силе, когда и при . Итак, правило Лопиталя-Бернули, когда оно применимо позволяет раскрыть неопределенности типов: и .

5) Сравнение при помощи правила Лопиталя-Бернули поведения при функции: показательно , степенной и логарифмической показывают, что показательная функция имеет более высокий порядок роста, чем степенная – более высокий порядок роста чем логарифмическая .

Другие типы неопределенностей.

1)

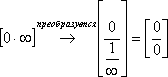или же 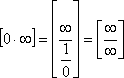и применяется правило Лопеталя-Бернули.

2) , если при , - ББ при , если же при , то имеем неопределенность типа . Неопределенности типов раскрываются с помощью предварительного логарифмирования и вычисления предела логарифма функции что приводит к неопределенности типа .

Примеры. 1)

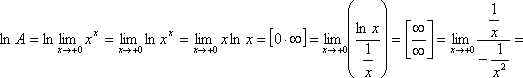
2)

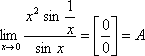
. Рассмотрим: 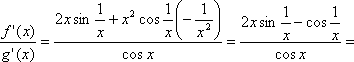|это отношение не имеет предела при | правило Лопиталя-Бернули не применимо. Найдем предел А непосредственно. 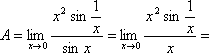0

58.Дифференциация функции и его приложение

Дифференциалом функции называется главная,линейная относительность дх часть приращения  функции,равная произведению производной на приращение независимой переменной. Дифференциал независимой переменной равен приращению этой переменной. Геометрически дифференциал (dy)- есть приращение касательной,проводимой к графику функции в точке х и может быть как меньше,так и больше приращется функции ду. Для линейной функции у=кх+в     Свойства дифференциала в основном аналогичны свойствам производной. 1)    dc=0 2)    d(cu)=c du 3)    d(u+(-)v)=du+(-)dv 4)    d(uv)=v du+u dv 5)    d(u)=vdu-udv            (v)        v(в квадрате)  

Применение Дифференциала в приближённых вычислениях. Приращение функции состоит из двух слагаемых,причём первое слагаемое есть бесконечно малая величина первого порядка.Произведение же есть величина бесконечно малая высшего порядка.Поэтому в приближённых вычислениях пользуются приближённым равенством. 59 билет. Производные высших порядков .Дифференциалы высших порядков .

Производные высших порядков. Рассмотрим функцию , определенную на некотором промежутке . Вычислим производную , которая также является функцией на . Производной второго порядка от функции называется производная от ее производной: . Аналогично определяют производную любого порядка: .

Дифференциалы высших порядков. Рассмотрим дифференциал функции в произвольной точке промежутка : . Здесь - приращение независимой переменной, которое является числом и не зависит от . Сам же дифференциал есть функция от , и можно вычислить дифференциал от этой функции: При этот дифференциал от дифференциала называется дифференциалом второго порядка и вычисляется по формуле Аналогично вычисляется дифференциал любого порядка .

60.Т. Ферма. y= f(x) диф на (а,b)=>непрер на (а,b). Пусть ·с принадлеж (а,b); ·с-наиб(наим) знач ф-ции на этом интервале, тогда f‘(с)=0. Док-во:наиб( наим-док-во наоборот): ·с-·наиб знач ф-ции на (а,b). 1.Пусть , тогда ≤f(с); -f(с) ≤0;≤0; lim= f₊‘(c) ≤0. 2. Пусть , тогда -f(с)≥0; ≥0; lim= f₋‘(c) ≥0; f₋‘(c)= f₊‘(c)=> f‘(c)=0.

61.Т.Ролля. Пусть f(x) непрер-на на отрезке [a,b]и диф-ма на интервале (a,b), а на концах отрезка ф-ция принимает одинаков. знач-я f(a)=f(b), тогда сущ-ет с,принадлежащее (a,b), такое, что f‘(c)=0. Док-во:m,M-наим и наиб знач ф-ции на отрезке [a,b]. 1.m=M=> f(x)-постоянная ф-ция=> f‘(c)=0. 2.m<M,тогда либо наим, либо наиб достиг-ся внутри интервала, но тогда на интервале (a,b) выполнены условия т. Ферма. И в точке наим(наиб) значения ф-ции произв-ная будет=0.