Вопрос 48. Непрерывность функции.

Определение 1.

Функция называется непрерывной в точке, если она удовлетворяет следующим трём условиям:

1. определена в точке 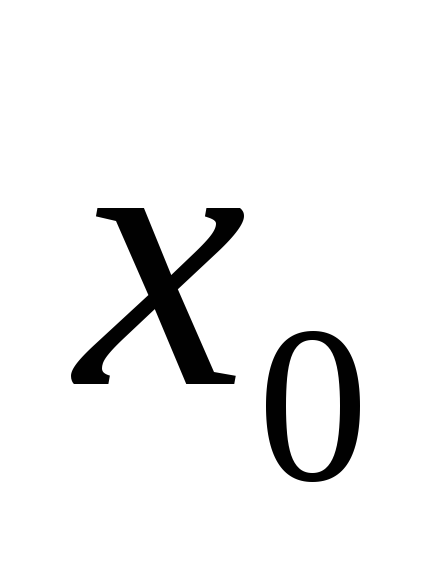(т.е. существует );

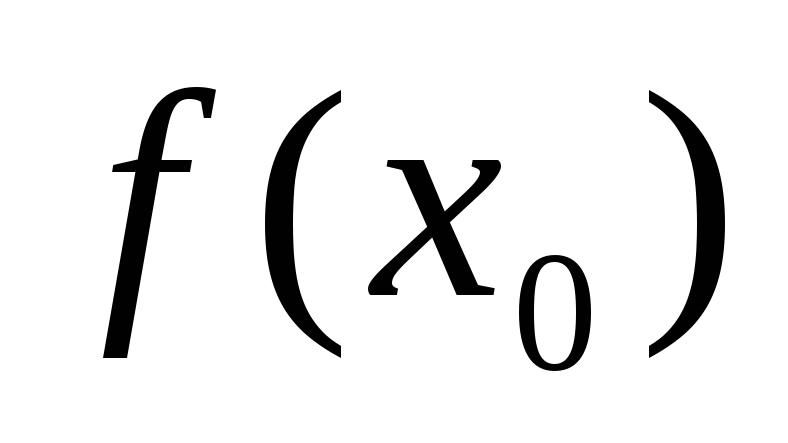2. имеет конечный предел ф-ии при ;

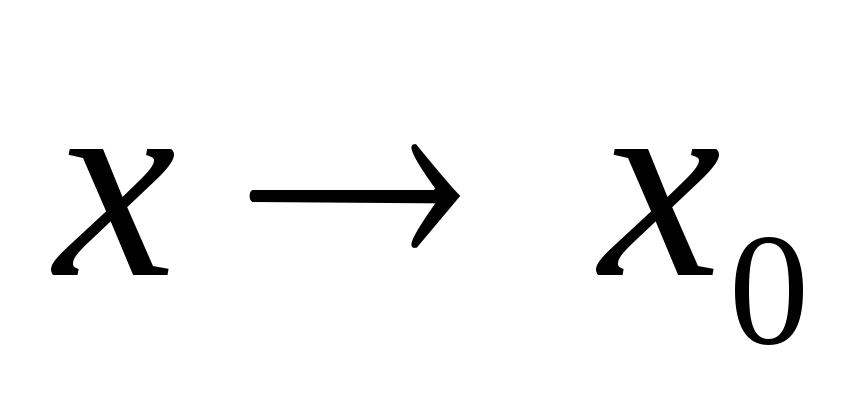3. этот предел = значению ф-ии в точке ,

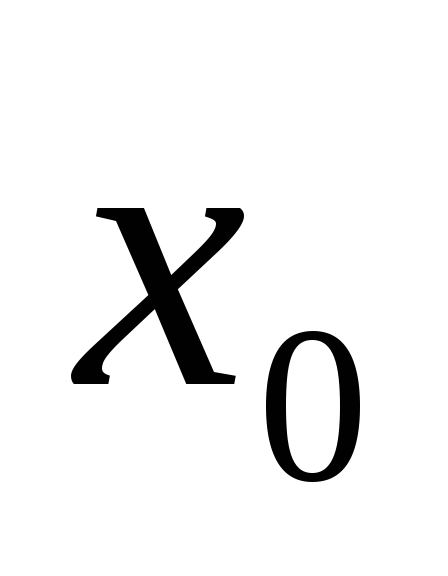т.е. .

Определение непрерывности ф-ии может быть записано и так: 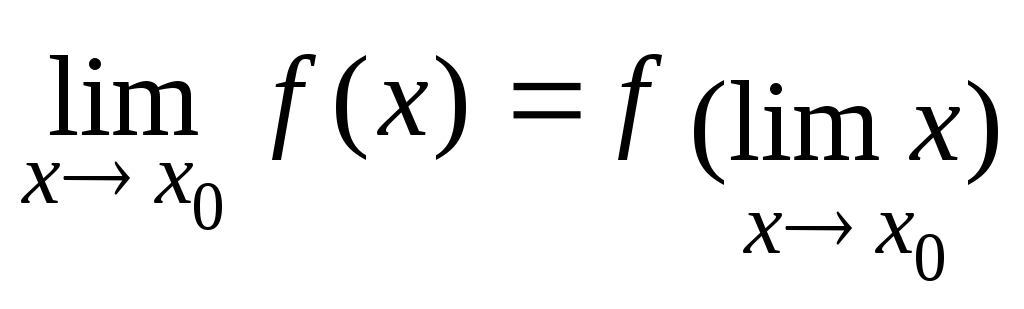, т.е. для непрерывной ф-ии возможна перестановка символов предела и ф-ии.

Дадим аргументу приращение . Тогда ф-ия получит приращение , определяемое как разность наращенного и исходного значения ф-ии: . Так, мы можем сформулировать определение 2:

Ф-ия называется непрерывной в точке , если она определена в этой точке и бесконечно малому приращению аргумента соответствует бесконечно малое приращение ф-ии:

Убедимся в равносильности 2х приведённых определений непрерывности. Из 1го определения согласно при следует , т.к. стремление равносильно условию .

На основании теоремы о связи бесконечно малых величин с пределами ф-ий можно записать , где есть бесконечно малая при , т.е. . Конец доказательства.

Точка называется точкой разрыва ф-ии , если эта ф-ия в данной точке не явл. непрерывной. Различают точки разрыва:

- первого рода (когда сущ-ют конечные односторонние пределы ф-ии слева и справа при , не равные друг другу. К этим точкам относятся точки устранимого разрыва (когда предел ф-ии при сущ-ет, но значению ф-ии в этой точке);

- второго рода (когда хотя бы 1 из односторонних пределов слева или справа =  или не существует).

Св-ва ф-ий, непрерывных в точке:

1. Если ф-и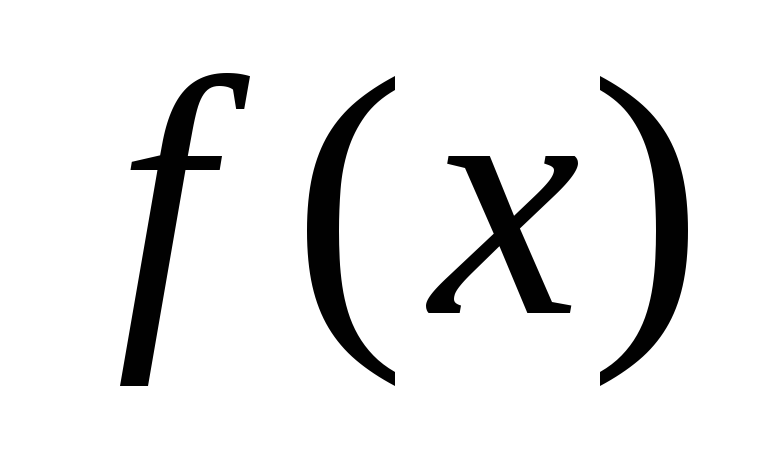и и 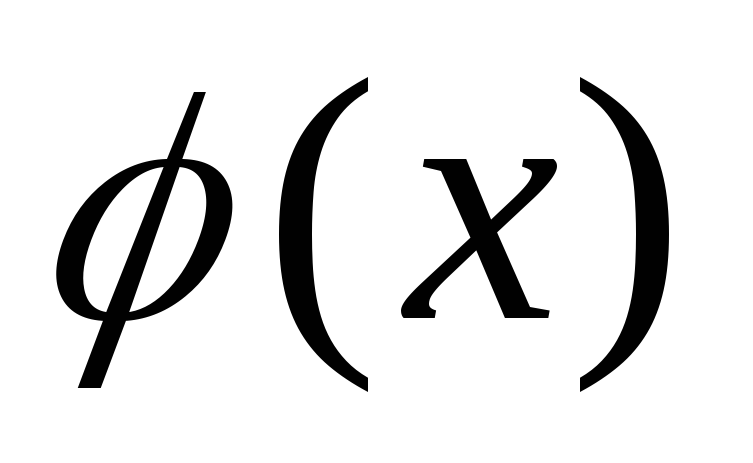непрерывны в точке 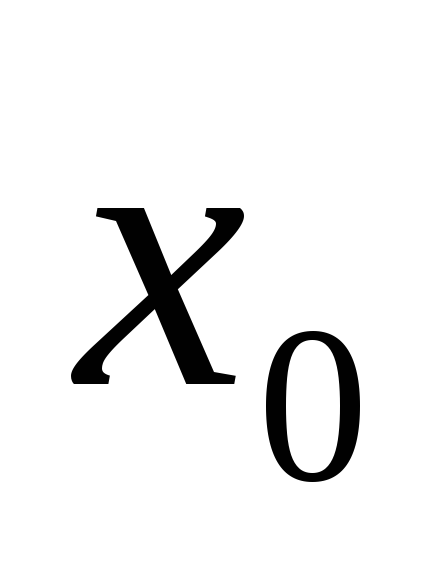, то их сумма, произведение и частное (при условии 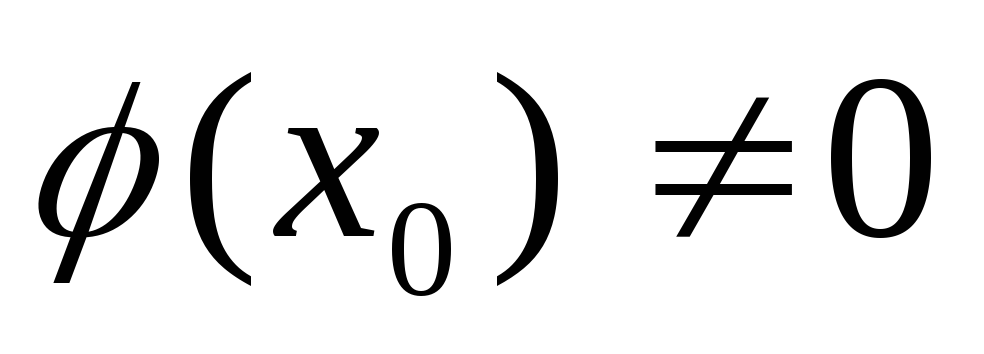) явл. ф-ями, непрерывными в точке 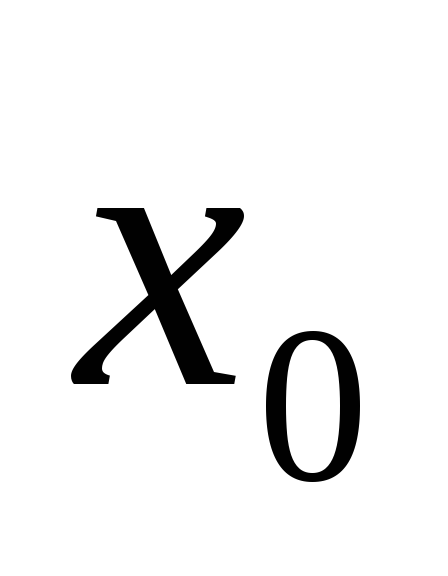. Док-во следует из определения непрерывности и аналогичных св-в пределов ф-ий).

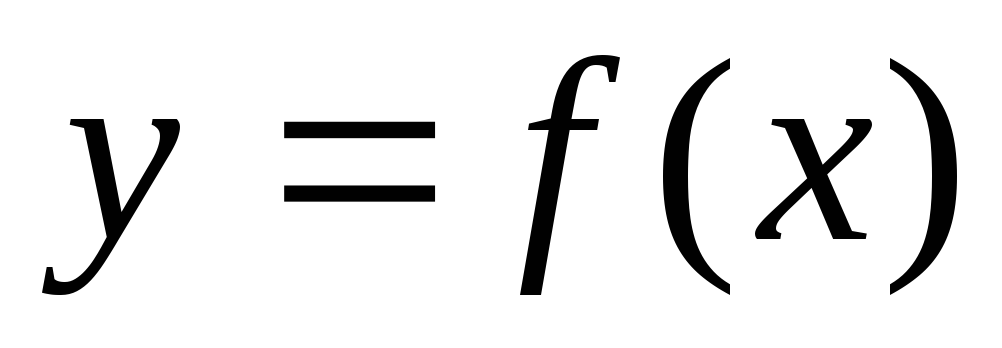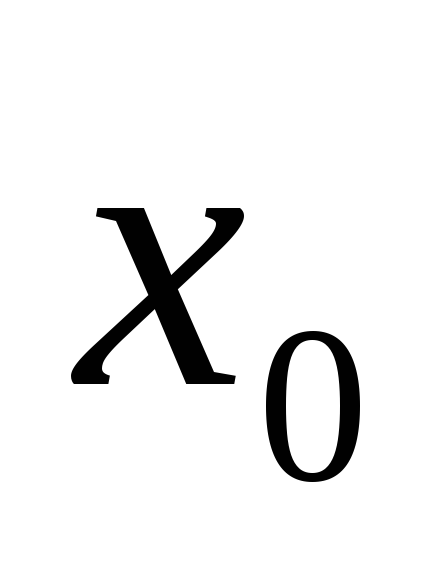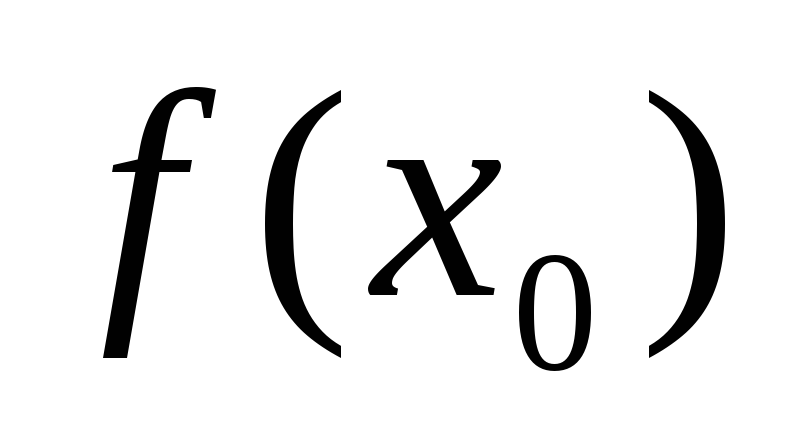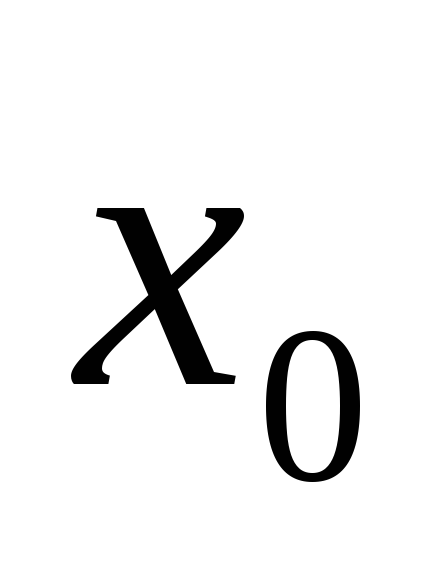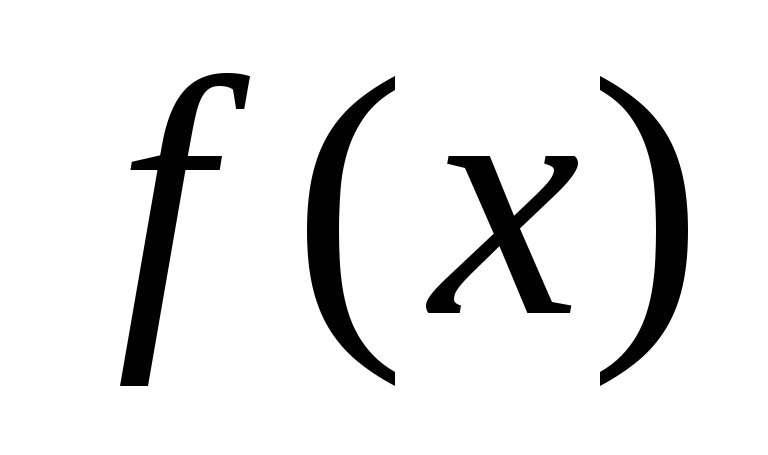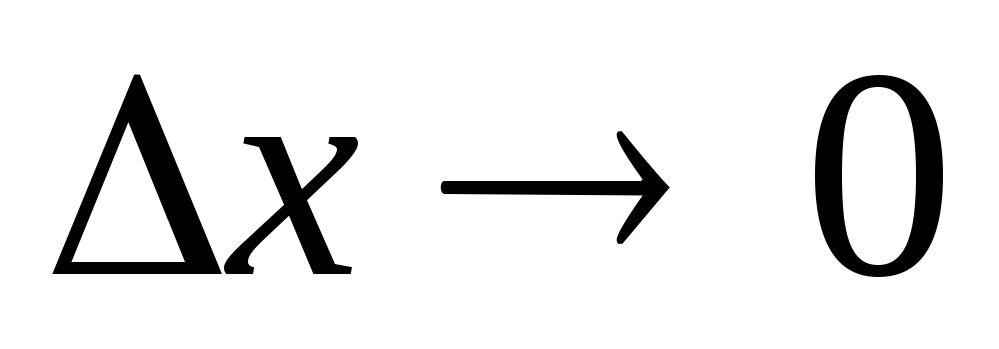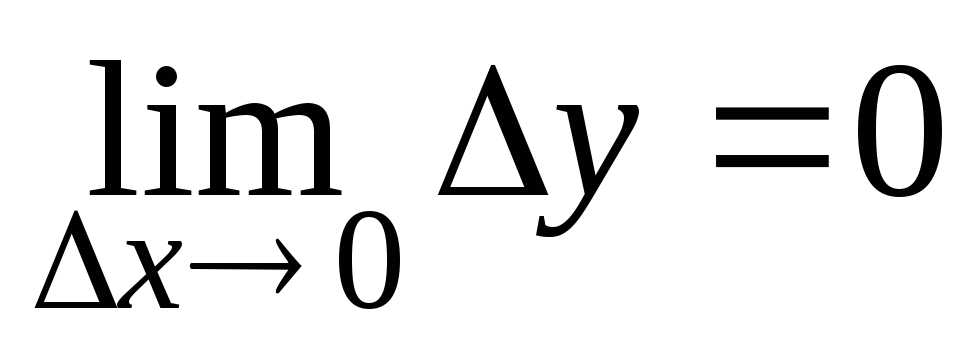2. Если ф-ия непрерывна в точке и > 0, то сущ-ет такая окрестность точки , в кот. > 0. Док-во этого св-ва основывается на том, что при малых приращениях аргумента в соотв. со 2м опред. непрерывности ф-ии () можно получить как угодно малое приращение ф-ии , так что знак ф-ии 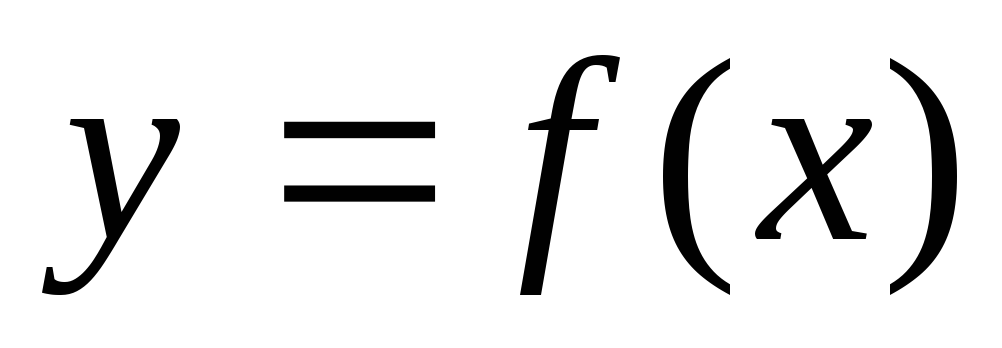в окрестности (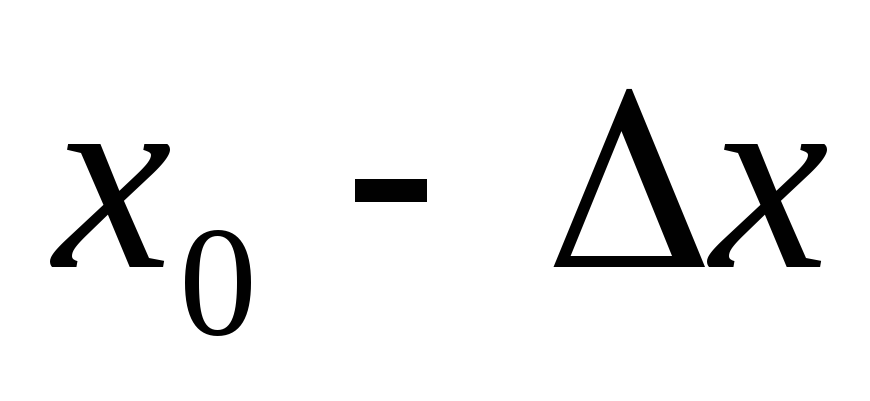, 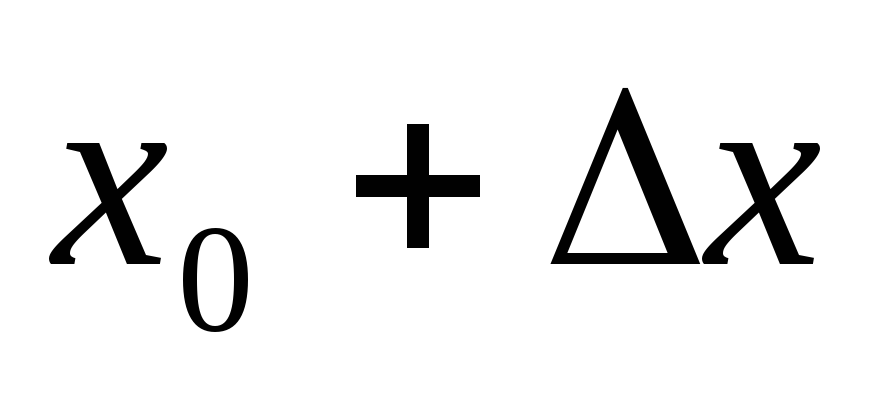) не изменится.

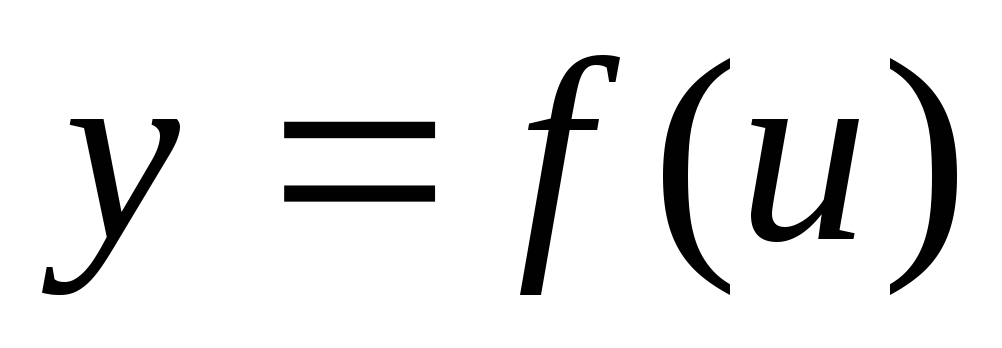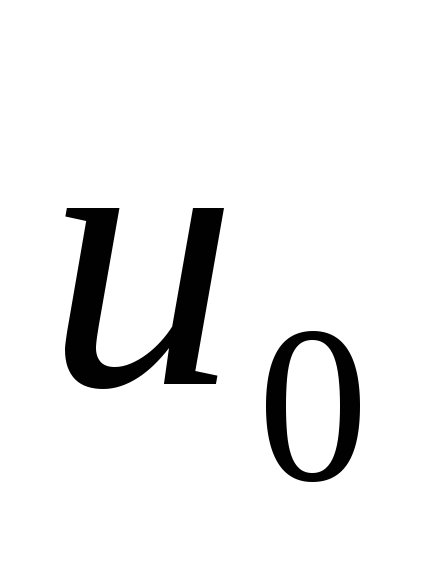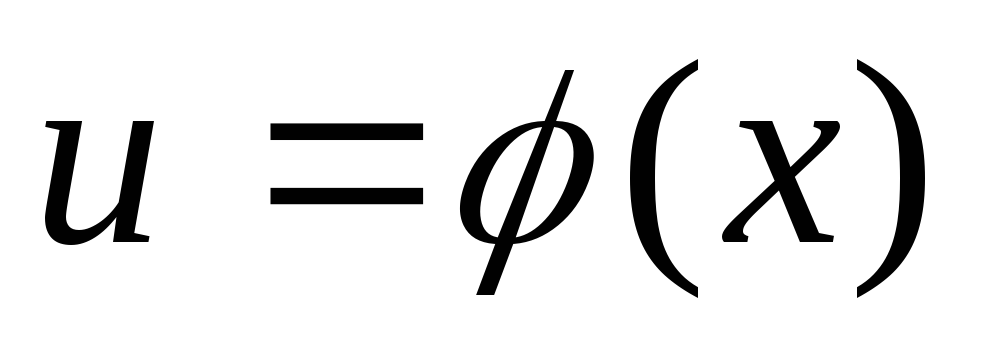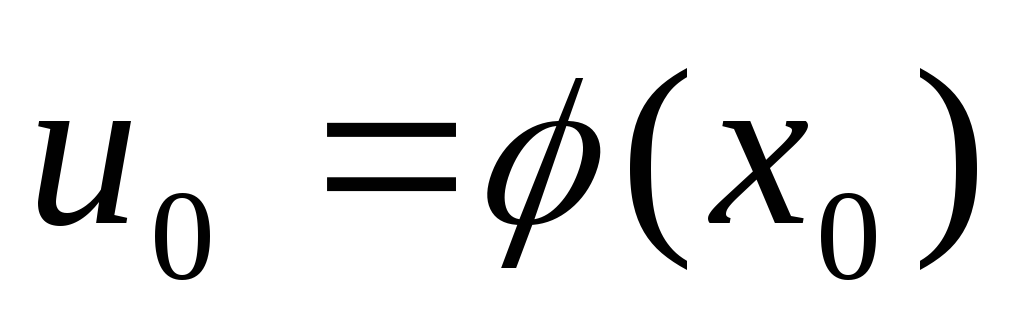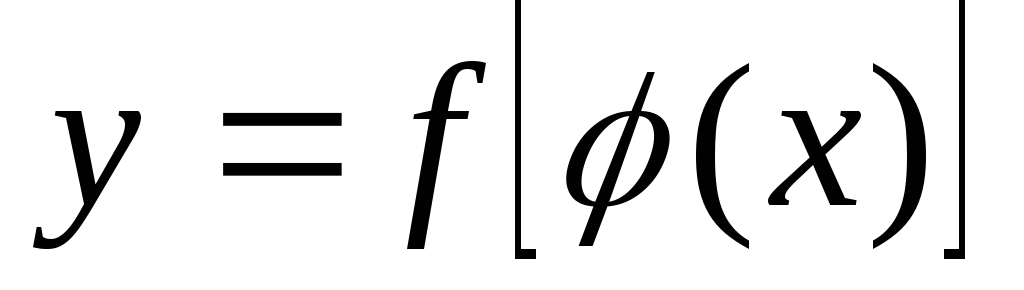3. Если ф-ия непрерывна в точке , а ф-ия непрерывна в точке , то сложная ф-ия непрерывна в точке 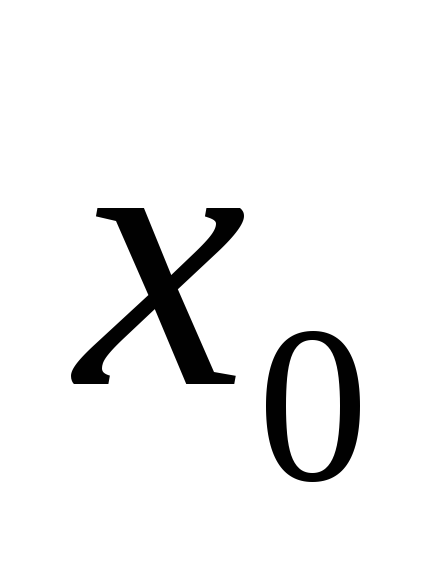. Док-во сост. в том, что малому приращению аргумента 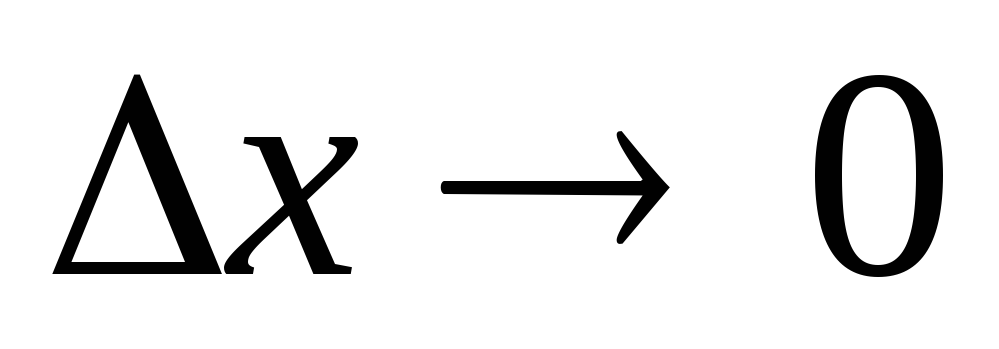в силу 2го опред. Непрерывности ф-ии (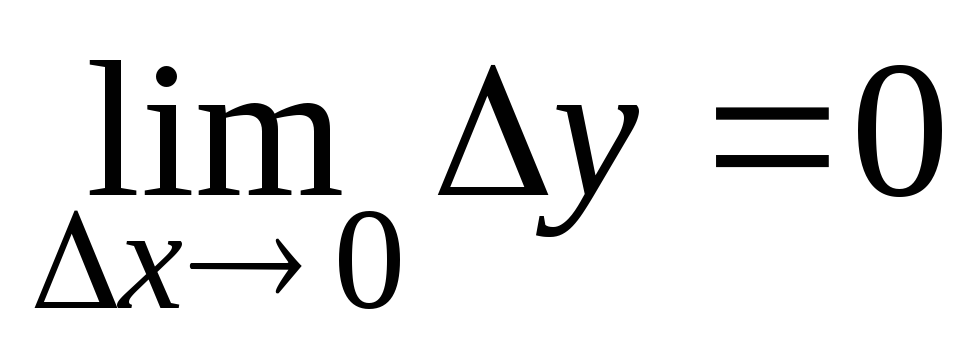) 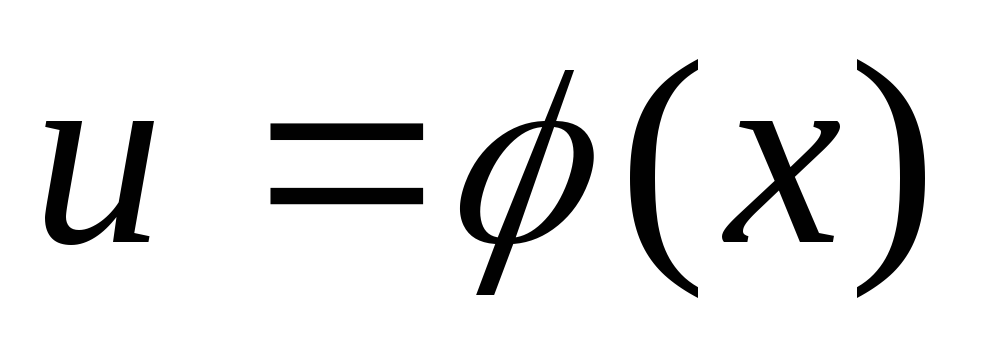соответствует как угодно малое приращ. 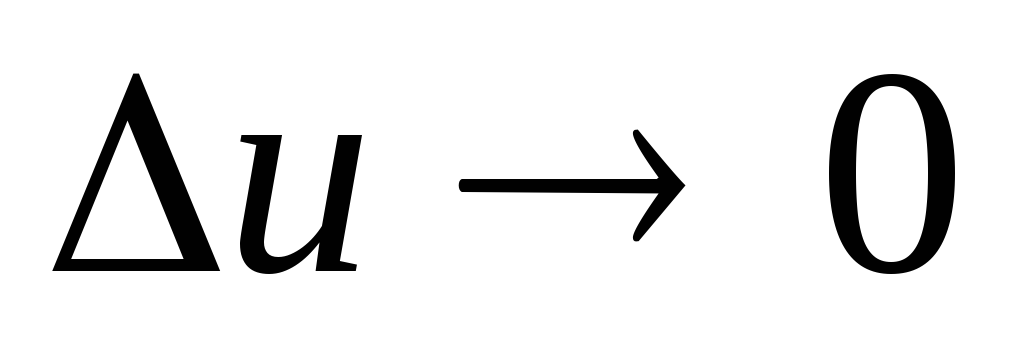, приводящее в свою очередь в силу того же определения непрерывности ф-ии 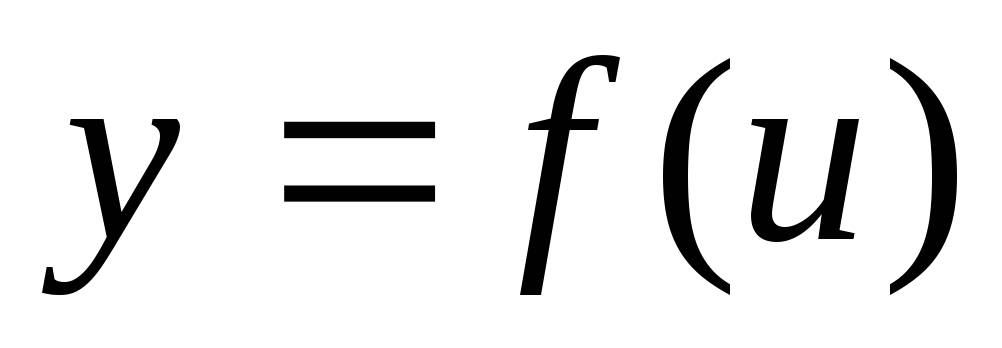к как угодно малому приращению 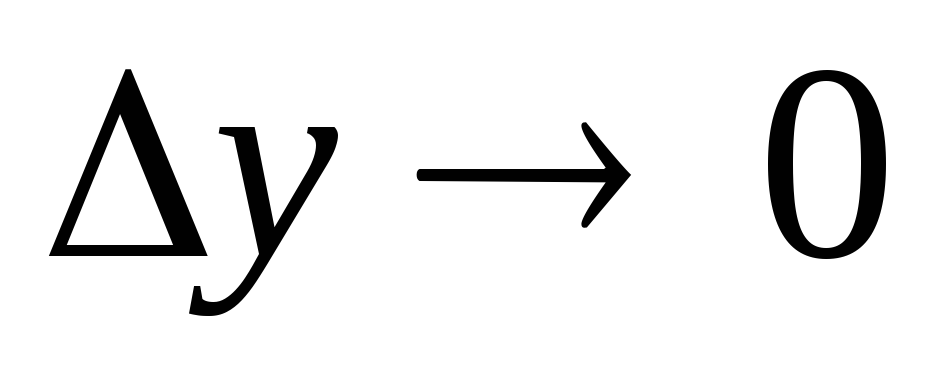. Это св-во мб записано в виде 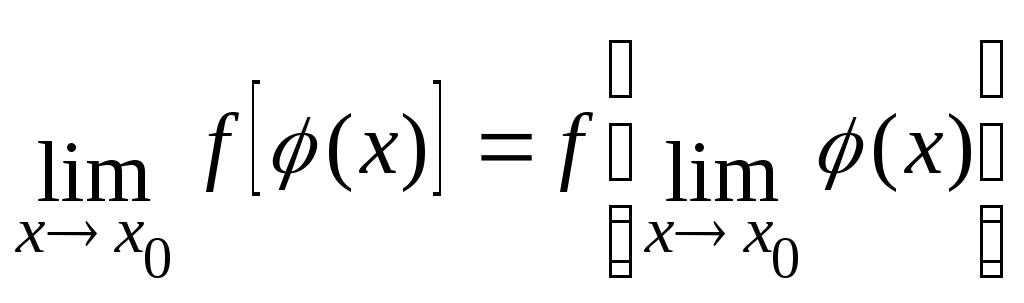, т.е. под знаком непрерывной ф-ии можно переходить к пределу.

Ф-ия называется непрерывной на промежутке Х, если она непрерывна в каждой точке этого промежутка. Все элементарные ф-ии непрерывны в области их определения.

Св-ва ф-ий, непрерывных на отрезке:

1. Если ф-ия 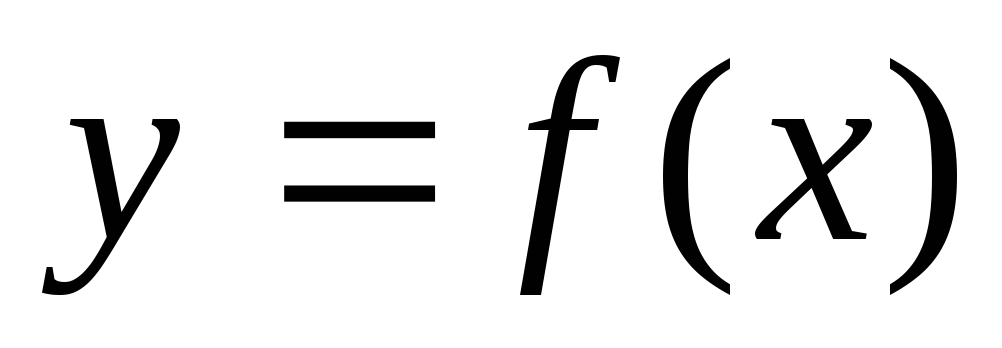непрерывна на отр. [a; b], то она ограничена на этом отр.

2. Если ф-ия 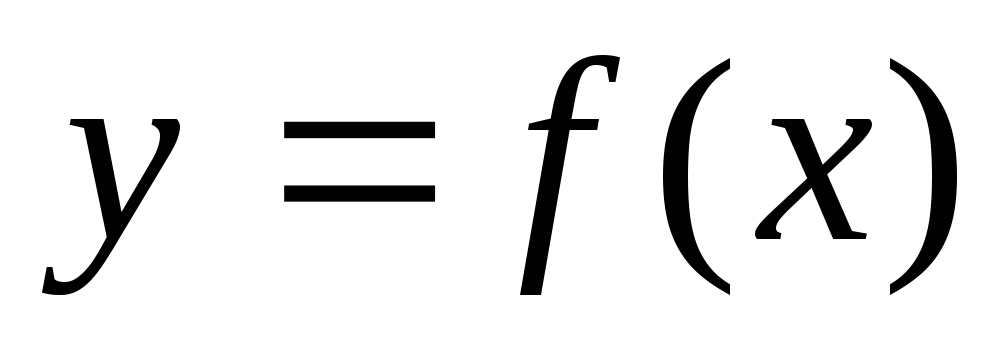непр. на отр. [a; b], то она достигает на этом отр. наим. знач. m и наиб. знач. M (теорема Вейерштрасса).

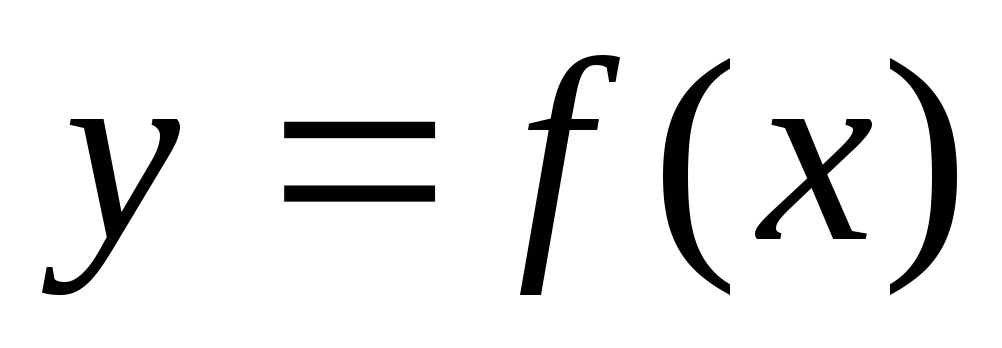3. Если ф-ия непрерывна на отр. [a; b] и значения ее на концах отр. 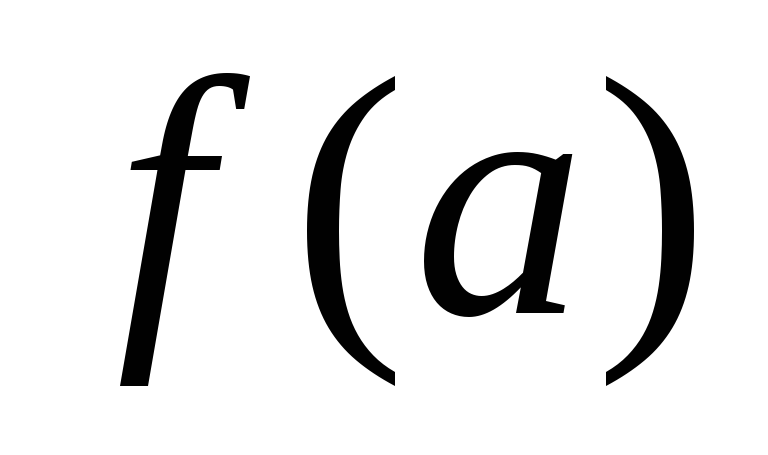и 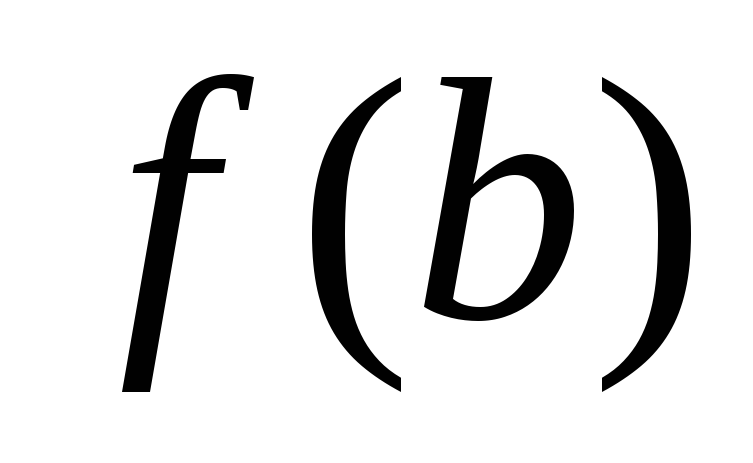имеют противоположн. знаки, то внутри отр. найдется точка 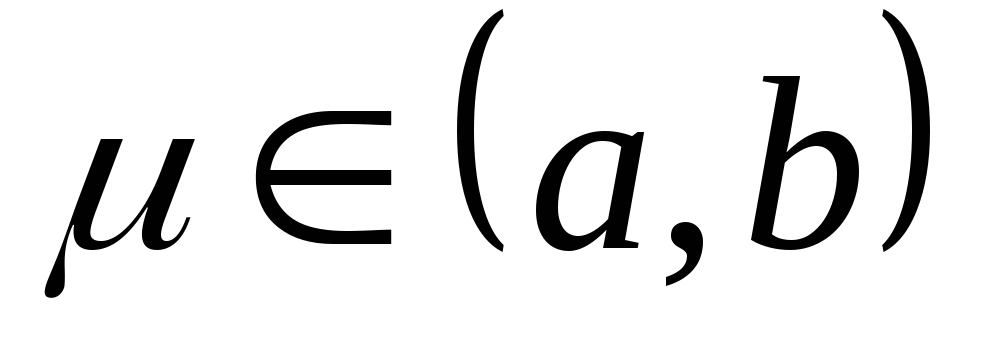, такая, что 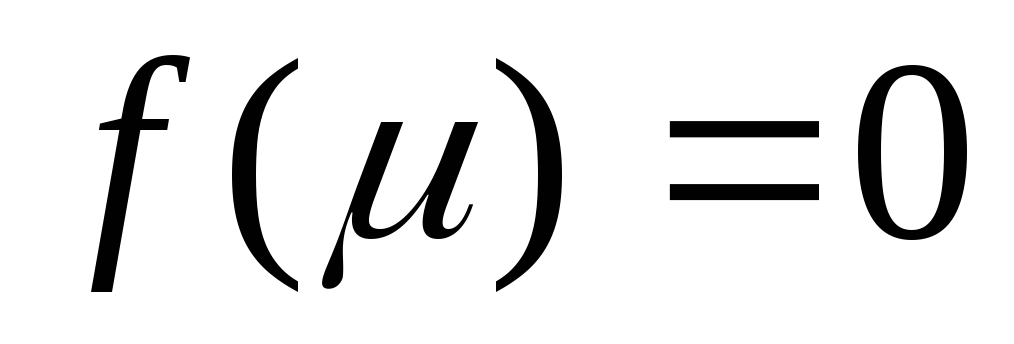(теорема Больцано-Коши).

Пусть функция определена на некотором полуинтервале , для которого -- левый конец. Функция называется непрерывной справа в точке , если существует предел при и этот предел равен значению , то есть Пусть, функция определена на некотором полуинтервале , для которого  -- правый конец. Функция называется непрерывной слева в точке , если существует предел при и этот предел равен значению , то есть