49 Вопрос
Точки разрыва функции, их классификации.
Точки, в которых
нарушается непрерывность функции,
называются точками
разрыва этой функции.
Все точки разрыва функции разделяются
на точки разрыва первого и второго рода.
Точка разрыва х0 называется точкой
разрыва первого рода
функции y=f(x),
если в этой точке существуют конечные
пределы функции слева и справа
(односторонние пределы), т.е.
1
и.
.
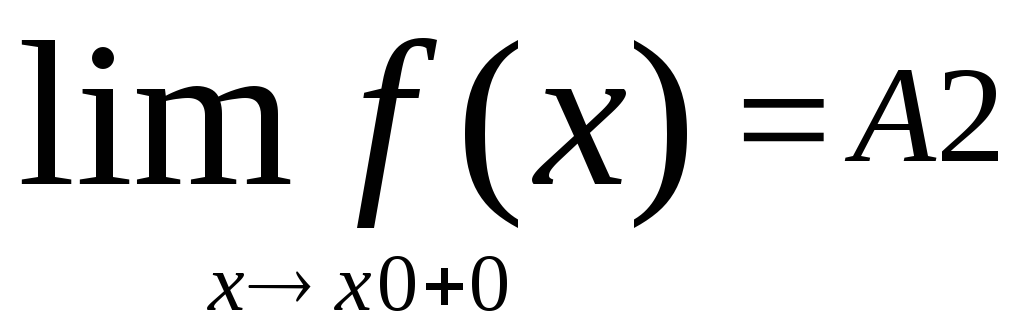При этом:
-
если А1=А2, то точка х0 называется точкой устранимого разрыва;
-
если А1
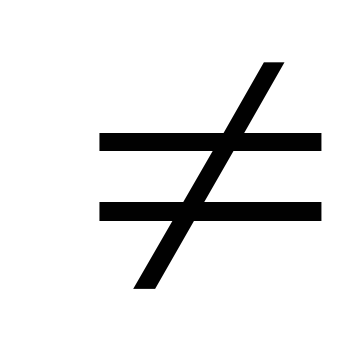А2,
то точка х0 называется точкой
конечного разрыва;
Величину
называют скачком функции в точке разрыва
первого рода.
Точка х0 называется точкой разрыва второго рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует или равен бесконечности.
Билет №50
Теорема(1-ая
теорема Больцано-Коши):
Пусть
непрерывна на отрезке [a,b]
и на концах отрезка приним. разные знаки
(
).
Тогда существ.
и
Док-во: разобъем
отр. [a,b]
на 2 равные части. Значения в этой толчке
либо=0, и тогда теорема док-на, либо оно
будет иметь знак, противополож. знаку
значения одного из концов. Выберем этот
отрез., на котор. ф-ия принимает разные
знаки. Положим:
-лев.конец,
-прав.конец,
и
,
и на отр.
ф-ия приним. значения противополож.знаков.
Раздел.отр.
пополам и выберем ту половину, на концах
котор.ф-ия приним.значения противополож.знаков.
Обозначим этот отр.
:
и
.
Продолжим этот процесс:
и т.д. до бесконеч. Всегда выпол.услов.:
.
Таким образом получ.послед.вложенных
отрезков:
.
Длина
и
.Рассмотр.лев.концы
отр-ов. Послед.:
всегда
монотонн.возраст. и огранич.сверху.,
след. сущ.
.
Аналогич. рассм.послед.прав.концов:
.Она
всегда монотонн.убыв. и огранич.снизу,
след. тоже имеет предел. Т.к. для люб. n:
,
знач.,
(
по теореме о предел.переходе в нер-во).
Т.к. предел
,
то:
(
по св-ву пределов). Отсюда след., что сущ.
точка
и для люб. n:
и точка
.
Ф-ия
непрерыв.на
отр. [a,b],
след. По опред.непрерыв.: бесконеч.малому
приращению аргументов точки с соотв.
Бесконеч.малое приращение ф-ии в точке
с. (
,
знач.
и
;
и
).
По теореме о постоян.знака непрерыв.ф-ии
сущ. интервал
,
на котор.ф-ия приним. тот же знак, что и
на конце
,
например
.
Сущ.интервал
,
на котор.ф-ия приним.тот же знак, что и
на конце
,
например
.
Положим
-бескон.малая
величина. Тогда
тоже бескон.малая величина, т.е.
.Отсюда
,
след.
.
Теорема(2-ая
теорема Больцано-Коши): Пусть
ф-ия
непрерыв.на
отр. [a,b]
и
.
Пусть A<C<B,
тогда сущ.
,
такое что
.
Док-во:
(опустим
на велич.с). Тогда
будет
на концах отр. [a,b]
приним.разные знаки.Тогда по 1-ой теореме
Больцано-Коши существ.
,
такая что
.
Т.е.
,
зн.
Теорема(1-ая
Вейерштрасса): Пусть
ф-ия
непрерыв. на отр.[a,b].
Тогда она ограничена на этом отр.
Рассмотр. Ф-ию:
,
Теорема(2-ая
Вейерштрасса): Пусть
ф-ия
непрерыв.на отр.[a,b].
Тогда она на этом отр.достигает своего
наибольш.и наименьш.значения.
Док-во: Сущ.
и
,
такие что
и
(точная
верх.и ниж.грани). Рассмотр. Ф-ию
на отр. [0,1]:
,
.
51.билет Пр-ная ф-ции,дифф-сть. Опр:f(x)опред на мн-ве Х; х0 принадлеж Х.Рассмотр приращ х в ·х0 ; х0+∆х принадлеж Х
∆ f= f(х0+∆х)- f(x0); (∆ f= f(х0+∆х)- f(x0))/ ∆х=∆ f/∆х
Сущ-ет lim
=
lim
=А=
f‘(х0)
Опр: f(x)диффер-ма в ·х0,если ее приращ f(х0+∆х)- f(x0)=А∆х+α(∆х)=А∆х+0(∆х)(рав-во №1), где А-пост. число, α(∆х)-бесконечно малое более высокого порядка, чем ∆х.
Т. Чтобы f(x)диффер
в х0, необх и достат, чтобы в х0 сущ. произв.
Док-во:необ-сть:пусть f(x) диф в х0,тогда
обе части рав-ва 1 разделим на ∆х, перейдем
к lim
=
lim
=A+
lim
=A
A= f‘(х0). Представим 1 в виде: f(х0+∆х)- f(x0)= f‘(х0)( ∆х)+0(∆х)
Дост-сть: в х0 сущ-ет
производн f‘(х0). Сущ-ет lim
=А;
=А+
,
=А
+
Т.Пусть f(x) диф-ма в х0,тогда она непрерывна в этой ·
Док-во.
=А
+
=(А+
.Если
Тогда
приращ тоже 