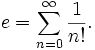- •14.Минор и алгебраическое дополнение
- •15. Свойства определителей.
- •16. Обратная матрица.
- •Вопрос 21
- •26.Уравнение плоскости в пространстве,различные виды.
- •30.Комплексные числа в тригонометрической и показательной форме
- •32.Понятие функции.График функции.
- •39.Косячный!!!Определение предела функции и его свойства.
- •Вопрос 48. Непрерывность функции.
- •49 Вопрос
- •Билет №52
- •53 Вопрос.
- •57.БилетЛогарифмическое дифференцирование.
- •58.Дифференциация функции и его приложение
- •62. Теоремы Лагранжа и Коши.
- •Вопрос 63
- •Вопрос 66. Признаки экстремума функции.
30.Комплексные числа в тригонометрической и показательной форме
Комплексные числа называют выражение вида z=x+iy,где х и у –действительные числа,а i-мнимая единица. Число х называется действительной частью числа z,а число у-мнимой частью числа z. Действительное число х является частным случаем комплексного при у=0.Комплексные числа являются действительными,т.е. при у не=0,называются мнимыми,а прих=0 у не=0,т.е. числа вида z =iy-чисто мнимыми. Комплексное число х-iу называют сопряженным с комплексным числом Z=x+iy и обозначается Z*=x-iy.Два комплексных числа называются равными,если равны их действительные и мнимые части. Сложение(вычитание) z1+(-)z2=x1+(-)x2+i(y1+(-)y2) Умножение z1z2= (x1x2-y1y2)+i(x1y2=x2y1) Деление z1=(x1x2=y1y2)+i(x2y1-x1y2)
)
(между ними дробная
черта)
z2
x2+y2
(z2 не=0) (x2,у2 в квадрате)
Тригометрическая формой
комплексного числа
r = /z/
больше или =0,ф=Аrg z.
Связь
между тригометрическими и показательными
функциями выражается формулой Эйлера.
е(в степени iф)=cosф+I sinф.От суда следует
показательная форма комплексного числа
( z=re
В этих формах легко проводить
операции умножение,деление,возведение
в степень,извлечение корня из комплексных
чисел.
Модуль и аргумент комплексных
чисел.
С каждой точкой z (х,у)
комплексной плоскости связан радиус-вектора
этой точки Оz(вектор,сверху стрелочка),длина
которого обозначается /z/
r =/z/= x2+y2(под корнем)
Угол ф,образованный радиусом-вектора
Оz(вектор) с осью Ох,называется Аргументом
комплексного числа z и обозначается
Arg z.
31.
![]() ограничен.сверху(снизу),
если существует такое число М(m),
такое что, для любого х не превосходит
М.
ограничен.сверху(снизу),
если существует такое число М(m),
такое что, для любого х не превосходит
М.
![]()
Всякое число М(m), ограничивающ.множество х сверху(снизу), наз.верхней (нижней) гранью множества х.
Множество наз.ограниченным, если оно огранич.и сверху и снизу.
Точной верхней гранью множества х обознач.супремум х, наз.наименьшая из верхних граней множества.
1)
![]()
2)
![]()
Точкой ниж.гранью inf x=m (инфимум)
1)
![]()
2)
![]()
![]() =
=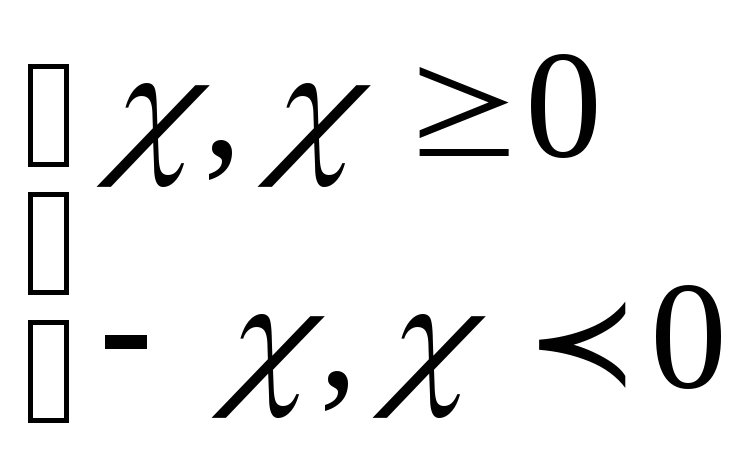
Свойства:
1)
![]()
2)
![]()
3)
![]()
32.Понятие функции.График функции.
Определение.Если каждому элементу х множества Х(х принадлежит Х)ставится в соответствие вполне определенный элемент у множества У(у принадл. У), то говорят, что на множества Х задана функция у=f(х)
При этом х называется независимой переменной (аргумент),у-зависимой переменной, а буква f обозначает знак соответствия.
Множество Х называется областью определения(существования)функции, а множество У-область значения функции.
Если множество Х специально не оговорено,то под областью определения функции подразумевается область допустимых значений независимой переменной х,т.е. множество таких значений х, при к-рых функция у=f(х) вообще имеет смысл.
Основные св-ва функции:1)четность нечетность 2)монотонность 3)ограниченность4)периодичность
33. N f(n); n принад.N---f(n)
Последовательность наз.ограниченной сверху(снизу), если множество ее значений огранич.сверху(снизу).
Последовательность ограниченная и сверху и снизу, газ.огранич.последовательностью.
Последовательность неограниченная сверху или снизу наз.бесконечно большой послед.
Последовательность наз.бесконечно большой, если для любого М больше 0 существ.N M бол.0 сущ.№N
Число а наз.пределом
последовательности
![]() при
n---к
бесконечности, если для любого
при
n---к
бесконечности, если для любого
![]() бол.0,
существ.N
бол.0,
существ.N
![]() .
Предел
.
Предел![]() стремящ.к бесконеч.=А, предел
стремящ.к бесконеч.=А, предел
![]() стремящ.к
бескон.=1.
стремящ.к
бескон.=1.
Док-во:
![]()
![]()
Если а является
пределом
![]() ,
то говорят, что сходится к числу а.
Последов.наз.бесконечно малой, если ее
предел при
,
то говорят, что сходится к числу а.
Последов.наз.бесконечно малой, если ее
предел при
![]() =0
=0
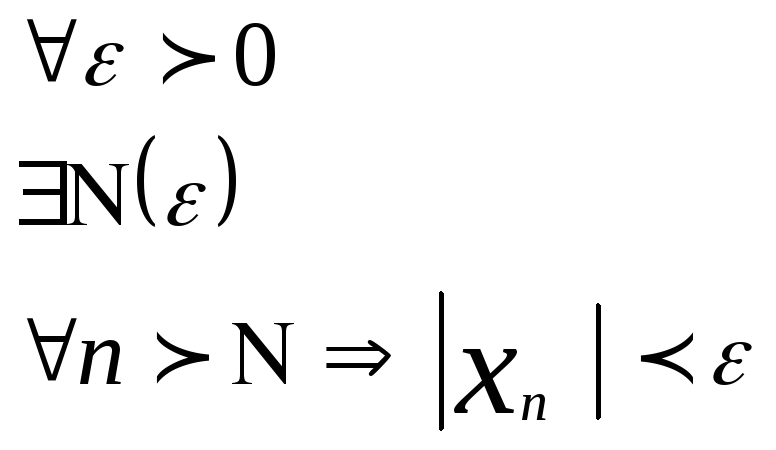
(![]() -А)
-А)![]() бескон.малая послед.;
бескон.малая послед.;
![]() при
при
![]()
№ 34 билет. Теоремы о пределах последовательности
Пусть послед Xn
имеет предел равный А (![]()
![]() ),а послед Yn
имеет придел равный B
(
),а послед Yn
имеет придел равный B
(![]() )
)
1.Сущ предел который
равен сумме пределов (![]() )
)
2.Предел произвед =произвед пределов
(![]() )
)
Следствие
![]() ,те
постоянную с можно выносить за знак
предела.
,те
постоянную с можно выносить за знак
предела.
3.Если B![]() ,
,![]()
Док-во: (только на второе он док-во дал почему-то)
![]()
![]()
![]()
![]()
+Из другой главы но похоже в эту же тему
Теорема о единственности предела последовательности:
Если послед имеет предел то он единственный
Док-во:
Предположим
![]()
![]()
0=![]()
Зн A-B
![]() ,раз A
и B
постоянные числа то следует что A=B
,раз A
и B
постоянные числа то следует что A=B
Билет №35 Св-ва бесконечно малых последовательностей. Последовательность Хn называется бесконечно малой если её предел равен 0. {Xn} ; /Xn/ ; ; А= (Xn-A)- бесконечно малая последовательность (Xn-A) - бесконечно малая последовательность {Xn-A}-бесконечно малая последовательность {Xn-A}={ A Теорема: тогда 1/ явл. Бесконечно большой последовательностью Доказательство: n / 1. Положим M=1/ , тогда модуль 1/ равен 1/модуль Теорема: Пусть , тогда Явл. Бесконечно малой последовательностью Доказ-во. / /= /2; / = /2 N= max( тогда одновременно выполняется и 1 и 2-е неравенство / / /+/ / ; Следствие: Сумма конечного числа бесконечно малых величин есть величина бесконечно малая. Следствие: С-действительное число(R) тогда С Теорема: Док-во: т.к / / ; / N= max( тогда одновременно выполняется и 1 и 2-е неравенство / /=/ // /
Билет №36. Теорема о сжатых последовательностях ( о двух милиционерах) Хn стремится к А при n ; Yn стремится к В при n Доказ-во: N=max (N1;N2) Теорема о единственности предела последовательности. Если последовательность имеет предел, то он единственный A= , Xn=A+ Xn=B+ 0=Xn-Xn= A+ B+ ; = (A-B стремится к 0 при n A=B
Билет № 37 Монотонные последовательности Последовательность Хn называется монотонно возрастающей или убывающей если для любого n выполняется неравенство Хn+1 Хn (Хn+1 Хn) Монотонно возрастающая или убывающая последовательности называются монотонными. Теорема: Монотонно возрастающая (убывающая), ограниченная сверху (снизу) последовательность имеет предел. Доказ-во: Пусть Хn+1 Хn; Хn M; т.к последовательность Хn ограничена, то она имеет точную верхнюю грань. ; Хn sup-супремум Хn, Хn Хn- монотонно возрастающая Хn т.е ; A= Теорема: Если последовательность имеет предел, то она ограниченная. Доказ-во: =А M=max(X1,X2…..Хn; А+ ) m=min(X1,X2…..Хn; А- ) тогда т.е. по определению это ограниченная последовательность.
№ 38 Число Е
Число Эйлера е - это основание натурального логарифма (значение: 2.71828182834905...), которое названо по имени швейцарского математика Леонарда Эйлера (1707-1783).
Натуральным логарифмом называется логарифм по основанию е. Он обозначается ln , т.е. log e N = ln N. Число е является иррациональным, его приближённое значение 2.718281828. Оно является пределом, к которому стремится число ( 1 + 1 / n ) n при неограниченном возрастании n ( см. так называемый второй замечательный предел в разделе "Пределы" ). Как это ни покажется странным, натуральные логарифмы оказались очень удобными при проведении различного рода операций, связанных с анализом функций. Вычисление логарифмов по основанию е осуществляется гораздо быстрее, чем по любому другому основанию
Свойства
Данное свойство играет важную роль в решении дифференциальных уравнений. Так, например, единственным решением дифференциального уравнения f''(x) = f(x) является функция f(x) = cex, где c — произвольная константа.
Число e иррационально и даже трансцендентно. Это первое число, которое не было выведено как трансцендентное специально, его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова.
eix = cos(x) + isin(x), см. формула Эйлера, в частности
![]()
Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса
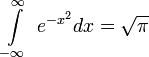
Способы определения
Число e может быть определено несколькими способами.
Через предел: (второй замечательный предел).
![]()
Как сумма ряда: