1. Вопрос

Множества. Способы задания множеств. Универсальное множество, пустое множество. Подмножества. Конечное, счетное и несчетное множества.

Основные определения    Под множеством будем понимать совокупность определённых вполне различаемых объектов, рассматриваемых как единое целое, это понятие – фундаментально.    Элементы множества – отдельные объекты, из которых состоит множество.    Для обозначения конкретных множеств используются заглавные буквы с индексом или без (A, X₁, Х₂), элементы множеств обозначаются строчными буквами (а, х₁, х₂). Общим обозначением служит пара фигурных скобок {}, внутри которых перечисляются элементы множества.    Принадлежность элемента множеству обозначается символом ∈, например, а∈S означает, что элемент а принадлежит множеству S. Запись х∉S означает, что х не из множества S.    Множества бывают конечными и бесконечными. Конечные множества – множества, в которых число элементов конечно. Бесконечные множества – бесконечное число элементов.    Множества задаются двумя способами: перечислением и описанием. Задание перечислением – перечисление всех элементов, составляющих множество. Он удобен для задания конечных множеств с небольшим количеством элементов и для задания множеств типа {2, 4, 6, 8…}.    Описательный способ задания множества состоит в том, что указывается характерное свойство, которым обладают все элементы множества. Например:

{x∈C | 0<x≤7} – множество {1, 2, 3, 4, 5, 6, 7}; {x | x – чётное} – множество чётных чисел; {x | x²-1=0} – множество {-1, 1}.

   Пустое множество – множество, не содержащее ни одного элемента, и обозначается Ø. Например:

{ x∈C | x²-x+1=0}=Ø.

   Введение понятия пустого множества позволяет оперировать с множеством каких-либо элементов, не заботясь о том, есть или нет в рассматриваемом множестве эти элементы. Пустое множество условно относится к конечным множествам.    Два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют собой одно и то же множество. Множества X и Y не равны (X≠Y), если либо в множестве Х есть элементы, не принадлежащие Y, либо в множестве Y есть элементы, не принадлежащие X. Символ равенства обладает следующими свойствами:

X=X – рефлексивность; если X=Y, то Y=X – симметричность; если X=Y и Y=Z, то X=Z – транзитивность.

   Из определения равенства следует, что порядок элементов в множестве несущественен, и множества {2, 3, 4} и {2, 4, 3} – одно и то же множество.

Понятие подмножества    Множество Х является подмножеством множества Y, если любой элемент множества Х принадлежит и множеству Y. Более краткая запись:

Х⊆Y

или если необходимо подчеркнуть, что в Y есть и другие элементы не из X:

Х⊂Y.

Свойства подмножества:

Х⊆Х (рефлексивность), [X⊆Y и Y⊆Z]→Х⊆Z (транзитивность). Ø⊂Х, где Х – любое множество.

Взаимно однозначное соответствие между множествами    Попарное соответствие между элементами двух множеств называется взаимно однозначным соответствием.    Общее число взаимно однозначных соответствий для n-элементных множеств:

n(n-1)…1=n!

Счётные и несчётные множества    Если множества являются бесконечными, то установление между ними взаимно однозначного соответствия наталкивается на трудности, связанные с необходимостью оперировать с бесконечно большим числом элементов множества. За основу для сопоставления бесконечных множеств принято брать натуральный ряд чисел N:

1, 2, …, n…

   Если бесконечное множество оказывается возможным привести во взаимно однозначное соответствие с натуральным рядом чисел, то такое множество называют счётным. Следует отметить, что не все бесконечные множества являются счётными. Если бесконечное множество невозможно привести во взаимно однозначное соответствие с натуральным рядом чисел, то его называют нечётным.    Существование несчётных множеств следует из теоремы, доказанной немецким математиком Г. Кантором: «Множество всех действительных чисел интервала 0<x≤1 несчётно».    Интервал (0, 1] может быть приведен во взаимно однозначное соответствие с любым другим интервалом (a, b]. Такое взаимно однозначное соответствие можно осуществить с помощью центральной проекции. Таким образом, несчётным является множество всех действительных чисел любого интервала (a, b].

Верхняя и нижняя граница множеств    Верхняя граница множества вещественных чисел S является число C такое, что для любого x∈S имеет место x≤C. Чисел, которые могут быть верхней границей множества, может быть бесконечное множество, а может и не быть вообще.    Точная верхняя граница (супремум) – верхняя граница, которая не превосходит любую другую. Обозначение – sup S. Любое множество может иметь только одну верхнюю границу.    Нижняя граница множества S – число c такое, что для любого x∈S имеет место x≥c. Точная нижняя граница (инфинум) – нижняя граница не меньшая любой другой нижней границы.

Универсальное множество    Если в некотором рассмотрении участвуют только подмножества некоторого фиксированного множества I, то это самое большое множество I называют универсальным множеством. Изображение универсального множества в виде областей в прямоугольнике называют диаграммой Эйлера-Венна.    Для универсального множества справедливо равенство:

X∪I=I

Универса́льное мно́жество — в математике множество, содержащее все мыслимые объекты. Универсальное множество единственно.

Универсальное множество обычно обозначается U (от англ. universe, universal set), реже E.

Свойства универсального множества

• Любой объект, какова бы ни была его природа, является элементом универсального множества.

• В частности, само универсальное множество содержит себя в качестве одного из многих элементов.

• Любое множество является подмножеством универсального множества.

• В частности, само универсальное множество является своим подмножеством.

• Объединение универсального множества с любым множеством равно универсальному множеству.

• В частности, объединение универсального множества с самим собой равно универсальному множеству.

• Пересечение универсального множества с любым множеством равно последнему множеству.

• В частности, пересечение универсального множества с самим собой равно универсальному множеству.

• Исключение универсального множества из любого множества равно пустому множеству.

• В частности, исключение универсального множества из себя равно пустому множеству.

• Исключение любого множества из универсального множества равно дополнению этого множества.

• Дополнение универсального множества есть пустое множество.

• Симметрическая разность универсального множества с любым множеством равна дополнению последнего множества.

• В частности, симметрическая разность универсального множества с самим собой равна пустому множеству.

2. Вопрос

Операции над множествами: объединение, пересечение, разность, дополнение. Свойства этих операций

.

Объединение множеств    Объединением множеств X и Y называют множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X, Y, т.е. принадлежат множеству Х или множеству Y. Объединение Х и Y обозначается через X∪Y. Формальное определение

X∪Y={x | x∈X или x∈Y}.

   Понятие объединения можно распространить на совокупность множеств. Обозначим через Ψ={X₁, …, X_n} совокупность n множеств X₁, …, X_n, называемую иногда системой множеств. Объединение этих множеств

представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств системы.    Свойства объединения множеств:

X∪Y=Y∪X (коммутативный закон); (X∪Y)∪Z=X∪(Y∪Z)=X∪Y∪Z (ассоциативный закон); X∪Ø=X.

Пересечение множеств    Пересечение множеств X и Y – множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству Х, так и множеству Y. Пересечение множеств X и Y обозначается через X∩Y. Формальное определение

X∩Y={ x | x∈X и x∈Y }.

   Операция пересечения позволяет установить ряд соотношений между двумя множествами.    Множества X и Y называют непересекающимися, если они не имеют общих элементов, т.е. если

X∩Y=Ø.

   Понятие пересечения можно распространить на совокупность множеств. Рассмотрим систему множеств Ψ={X₁, …, X_n}. Пересечение этих множеств

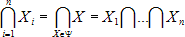
представляет собой множество, элементы которого принадлежат каждому из множеств системы Ψ.    Свойства пересечения множеств:

X∩Y = Y∩X (коммутативный закон); (X∩Y)∩Z=X∩(Y∩Z)=X∩Y∩Z (ассоциативный закон); X∩Ø=Ø.

Разность множеств    Разность множеств X и Y – множество, состоящее из всех тех и только тех элементов, которые принадлежат X и не принадлежат Y. Разность определяется только для двух множеств. Обозначение – X\Y. Формальное определение:

X\Y={ x | x∈X и x∉Y }.

Дополнение множества    Множество  , определяемое из соотношения

называют дополнением множества Х (до универсального множества I). Свойства дополнения множества:

X∩ =Ø, X∪ =I.

   Стоит заметить, что дополнением   является как X, так и   , следовательно

=X

   С помощью операции дополнения можно определить разность множеств:

X\Y={ x | x∈X и x∉Y }={ x | x∈X и x∈  }, X\Y= X∩ .

3. Вопрос

Числовая прямая. Числовые промежутки. Е-окрестность. Модуль действительного числа и его свойства.

Числовая прямая - это множество действительных чисел.

Геометрической моделью числовой прямой служит координатная прямая.

Множество действительных чисел - это вместе взятые множества рациональных и иррациональных чисел.

Действительное число или как его еще называют вещественное число - это любое положительное число, отрицательное число или нуль.

Действительные числа разделяются на рациональные и иррациональные.

Вещественные (действительные) числа - это своего рода математическая абстракция, служащая для представления физических величин. Такие числа могут быть интуитивно представлены как отношение двух величин одной размерности, или описывающие положение точек на прямой. Множество вещественных чисел обозначается и часто называется вещественной или числовой прямой. Формально вещественные числа состоят из более простых объектов таких, как целые и рациональные числа.

Множество действительных чисел изображается всей координатной прямой. Его называют числовой прямой. Обозначается она так:

                        (- ∞; + ∞)

Числовые промежутки

Числовые отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками.

Неравенство, задающее числовой промежуток	Обозначение числового промежутка	Название числового промежутка	Читается так:
a ≤ x ≤ b	[a; b]	Числовой отрезок	Отрезок от a до b
a < x < b	(a; b)	Интервал	Интервал от a до b
a ≤ x < b	[a; b)	Полуинтервал	Полуинтервал от a до b, включая a.
a < x ≤ b	(a; b]	Полуинтервал	Полуинтервал от a до b, включая b.
x ≥ a	[a; + ∞)	Числовой луч	Числовой луч от a до плюс бесконечности
x > a	(a; + ∞)	Открытый числовой луч	Открытый числовой луч от a до плюс бесконечности
x ≤ a	(- ∞; a]	Числовой луч	Числовой луч от минус бесконечности до a
x < a	(- ∞; a)	Открытый числовой луч	Открытый числовой луч от минус бесконечности до a

Представим на координатной прямой числа a и b, а также число x между ними.

 

Множество всех чисел, отвечающих условию a ≤ x ≤ b, называется числовым отрезком или просто отрезком. Обозначается так:

                        [a; b]

Читается так: отрезок от a до b.

Множество чисел, отвечающих условию a < x < b, называется интервалом. Обозначается так:

                        (a; b)

Читается так: интервал от a до b.

Множества чисел, отвечающих условиям a ≤ x < b или a < x ≤ b, называются полуинтервалами. Обозначения:

Множество a ≤ x < b обозначается так:

[a; b)

читается так: полуинтервал от a до b, включая a.

Множество a < x ≤ b обозначается так:

(a; b]

читается так: полуинтервал от a до b, включая b.

Теперь представим луч с точкой a, справа и слева от которой - множество чисел.

Множество чисел справа от точки a, отвечающих условию x ≥ a, называется числовым лучом.

Обозначается так:

                        [a; + ∞)

Читается так: числовой луч от a до плюс бесконечности.

Множество чисел справа от точки a, отвечающих неравенству x > a, называется открытым числовым лучом.

Обозначается так:

                        (a; + ∞)

Читается так: открытый числовой луч от a до плюс бесконечности.

Множество чисел слева от точки a, отвечающих условию x ≤  a, называется числовым лучом от минус бесконечности до a.

Обозначается так:

                        (- ∞; a]

Читается так: числовой луч от минус бесконечности до a.

Множество чисел слева от точки a, отвечающих неравенству x < a, называется открытым числовым лучом от минус бесконечности доa.

Обозначается так:

                        (- ∞; a)

Читается так: открытый числовой луч от минус бесконечности до a.

ε-окрестность

Пусть ε > 0 произвольное фиксированное число.

Окрестностью точки x₀ на числовой прямой (иногда говорят ε-окрестностью

называется множество точек, удаленных от x₀ не более чем на ε, т.е. O_ε(x₀) = {x: | x − x₀ | < ε}.

В многомерном случае роль окрестности выполняет открытый ε-шар с центром в точке x₀.

Модуль действительного числа и его свойства

Модулем действительного числа называется расстояние от начала отсчета до точки, соответствующей этому числу.  Обозначают модуль числа х, так: | х |. Очевидно, что | 0 | = 0.

Если число х больше 0, то | х | = х, а если х меньше 0, то | х | = - х. На этих свойствах модуля, основано решение многих уравнений и неравенств с модулем.

Короче это записывают так:

Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули:

|-а| = |а|

Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков:

|0| = 0

4. Вопрос

Определение числовой последовательности. Понятие об ограниченной и монотонной последовательности.

Определение. Пусть каждому натуральному числу n поставлено в соответствие некоторое единственное действительное число  (при этом разным натуральным числам n могут соответствовать и одинаковые действительные числа). В этом случае на множестве натуральных чисел определена функция:  , которая называется числовой последовательностью или просто последовательностью.

Последовательность обозначается:  , n=1, 2,… или  .

Числа  ,  ,… называются членами последовательности или ее элементами,  – общим членом последовательности, n – номером члена  .

По определению любая последовательность содержит бесконечное множество элементов.

Часто последовательность задается при помощи формулы:  ,  . В этом случае эта формула называется формулой общего члена последовательности { }. Например,  = , ;

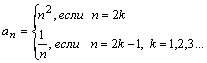
Последовательность может быть задана и другими способами. Например, если   – число всех различных делителей числа n, то  ,  - последовательность, для которой  =1,  =2,  =2,  =3,  =2,  =4,  =2,…

Для задания последовательностей используют также рекуррентные соотношения. При таком способе задания последовательности указывают один или несколько первых ее членов и формулу, которая позволяет найти ее n-й член через предшествующие члены. Например,

a =1, a =  +1 при n=1, 2,…;

b =1, b =2, b =2b +b  при n 3.

Определение. Пусть даны две числовые последовательности {a } и {b }. Суммой, разностью, произведением и частным этих последовательностей называются соответственно последовательности { }, {  }, { }, { }; последнее при условии, b 0, n=1, 2,…. Произведением последовательности {a } на число k, называется последовательность {ka }.

Определение. Последовательность {a } называется возрастающей (убывающей), если для любого n N справедливо неравенство a >a  (a <a ). Последовательность {a } называется неубывающей (невозрастающей), если для любого n N справедливо неравенство a a  (a a ).

Определение. Последовательности убывающие, возрастающие, неубывающие, невозрастающие называются монотонными последовательностями. Например, а) последовательность a =n!, n N –возрастающая; б) последовательность 1, 2, 3, 3, 4, 5, 6, 6, 7, 8, 9, 9,…- неубывающая; в) последовательность 1,  , 3,  , 5,  , 7,  ,…  – немонотонная.

Следует различать последовательность {a }, то есть множество элементов a , n N (оно всегда бесконечно) и множество значений ее элементов. Например, для последовательности {(-1) } множество значений ее элементов состоит из двух чисел –1 и 1.

Определение. Последовательность называется ограниченной сверху (снизу), если множество значений ее элементов ограничено сверху (снизу).

Определение. Последовательность, ограниченная сверху и снизу, называется ограниченной.

Например, последовательность {(-1) } ограниченная; последовательность {n} – ограничена снизу, но не ограничена сверху, следовательно, она неограниченная.

Наименьшее из чисел, ограничивающих последовательность {a } сверху, называется ее супремумом и обозначается supa , а наибольшее из чисел, ограничивающих последовательность снизу, называется ее инфимумом и обозначается infa .

1)Последовательность {x_n}  называется возрастающей,  если  .

2) Последовательность {x_n}  называется неубывающей, если  .

3) Последовательность {x_n}  называется убывающей, если  .

4) Последовательность {x_n}  называется невозрастающей, если  .

5. Вопрос

Определение предела числовой последовательности. Сходящаяся последовательность. Теорема о сходимости монотонной и ограниченной последовательности.

Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.

Число а называется пределом числовой последовательности {x_n}, если для любого положительного числа  ε существует номер N такой,  что при всех n>N  выполняется неравенство  .

Обозначение:   или  .

Последовательность, имеющая предел называется сходящейся, не имеющая его – расходящейся.

 

Верхний предел последовательности — это наибольшая из её предельных точек.

Нижний предел последовательности — это наименьшая из её предельных точек.