№1. Множества и операции над ними.

Множества – это совокупность элементов, объединённых по какому-либо общему признаку. Множесто А считается заданным, если для любого элемента а из множества А всегда можно определить, принадлежит элемент а этому множеству или нет. Множество, не содержащее ни одного элемента, называется пустым и обозначается Ø. Например, множество действительных корней уравнения х²+1=0 есть пустое множество. Если множество В состоит из части элементов множества А или совпадает с ним, то множество В называется подмножеством множества А и обозначается В С А. Два множества называются равными, если они состоят из одних и тех же элементов. Объединение двух множеств А и В называется множество С, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств, т.е. С=АUВ

А, В, С - множества

аА; А=…

А=х; х0

АВ, А является подмножеством множества В

-весь, всякий, каждый

-существует, !- существует и единственный

=> -следует, <=>- тогда и только тогда

- множество, которое не содержит ни одного элемента

 А: А – для любого множества А любое пустое множество является подмножеством множества А

1. АВ=С - объединение множеств

2. АВ=С - пересечение множеств

3. А/(наоборот линию)В=С - множество, элементы которого принадлежат множеству А, но не принадлежат множеству В

4. А х В={(а, в); аА} – множество упорядоченных пар

вВ

5. А х ВВ хА

Пример

А={1, 2, 3}; В= {4, 5}

А х В= {(1;4) (1;5) (2;4) (2;5) (3;5)}

Свойства над операциями.

• АВ=ВА

• АВС=А(ВС)

• АВС=А(ВС)

• АВ=ВА

• (АВ)С=(АС)(ВС)=АСВС

№2. Вещественные числа, их свойства, n- мерное арифметическое пространство.

R - множество всех действительных чисел

а,в R а+в R ахв R

а R ; ах=1

а, в R, ав : => ав; ва

ав; вс => ас – свойство транзитимности

а,в ; ав с R : асв

--------------------.------------.------- R вещественная или действительная прямая

0. 1

R; RхR= {(х;у); ху R}= двухмерное пространство

х R={(х; у; z); ху R}

= х R={(…….); ……. R} координаты точек в N-мерном пространстве

А, В  ; а=(…)

в=(....)

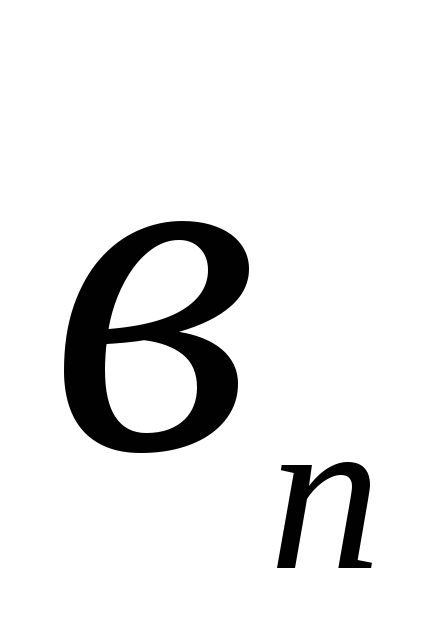d(A;B)=( -)+…………. (-) -расстояние между точками

метрика

R –мерное координатное пространство - совокупность всех n-мерных векторов, рассматриваемая с определёнными в ней операциями сложения векторов и умножения вектора на число.

В пространстве имеется система векторов, которая называется «диагональной»

Е1= (1,0……0) 1-линейно независима

Е2=(0,1……..0) 2-каждый n-мерный вектор разлагается по векторам диагональной

Еn=(0,0………1) системы

Базис пространства - система n-мерных линейно независимых векторов, если каждый вектор из пространства разлагается по векторам этой системы.

Размерность пространства - число векторов в любом его базисе.

№3. Связные и свободные векторы, их свойства.

А, В

• Направленный отрезок прямой, выходящий из т. А в т.В, называется связным вектором.

А

В

• Координатами 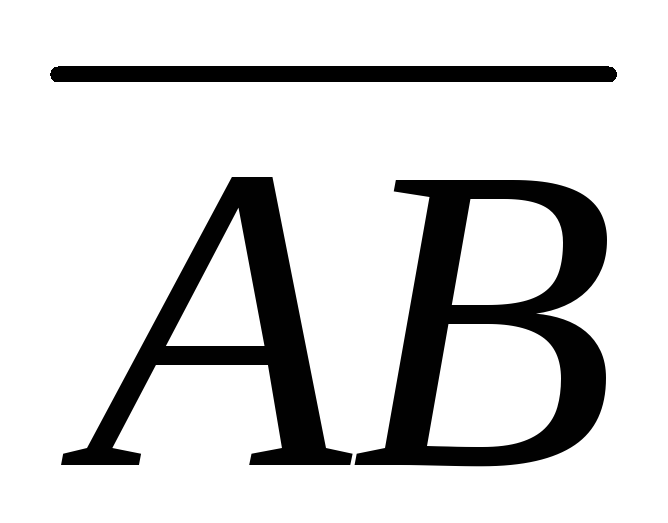называется упорядоченный набор чисел ((-),……(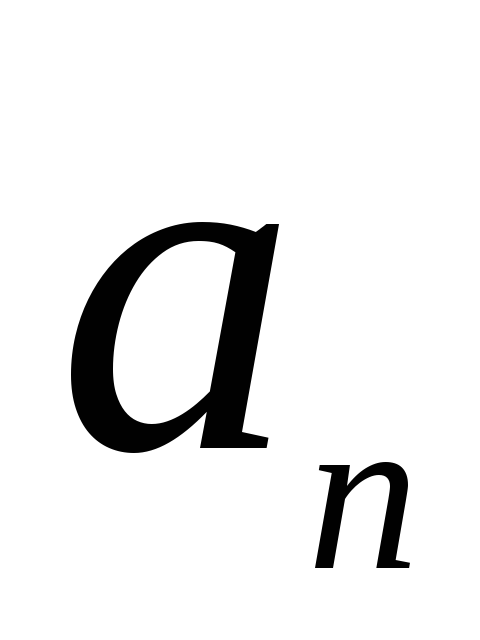-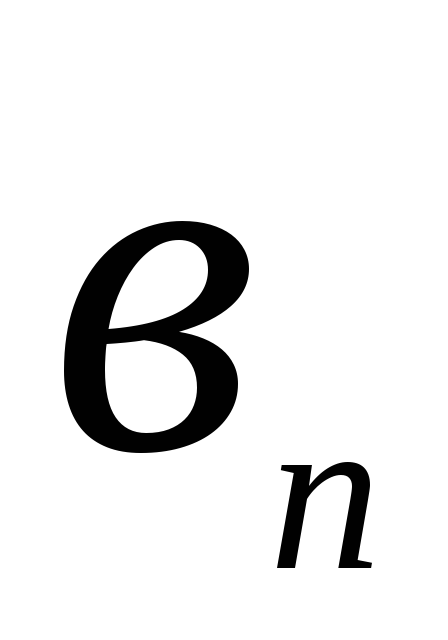))R

• Длиной 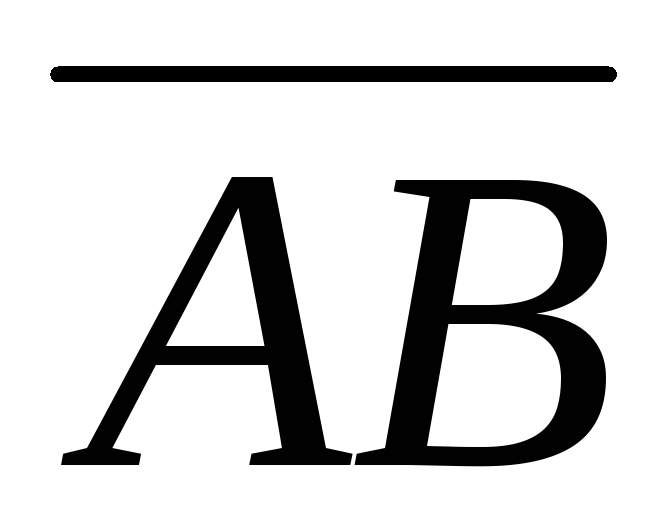обозначается

=( -)+…….(-)

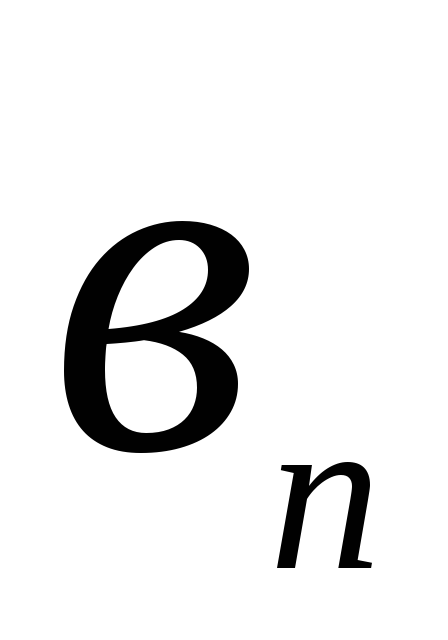• Совокупность всех векторов, имеющих одинаковые координаты называется свободным вектором.

-свободный вектор

а=(….)

4. Линейные операции над векторами

Операции сложения векторов и умножения на число, называются Линейными операциями.

Так как операции над ними сводятся к операциям над действительными числами.

5. Скалярное произведение векторов, угол между векторами.

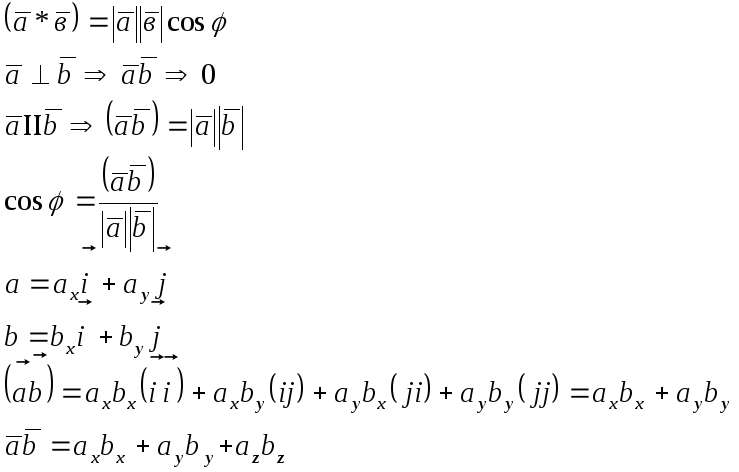
6. Базис в пространстве. Разложение вектора по базису R.

Система n—мерных лин. независимых векторов называется базисом Rⁿ (R²-плоскость,R³-пространство), если каждый вектор этого пространства R разлагается по векторам этой системы. Базисом называется совокупность всех лин. независимых векторов системы пространства. Скалярным произведением 2-х векторов а ив называется число, равное произведению модулей, перемноженных на cos угла между ними: а ва в Cos, где -угола междув. Скалярное произведение может быть найдено также по формуле: а в =а  пр._а в =в пр._в а скалярное произведение 2-х векторов равно произведению модуля одного из них на проекцию на него другого вектора. Свойства скалярного произведения: 1)Переместительное (ав=в а); 2)Сочетательное относительно числового множителя ((а в)=а в); 3)Распорядительное ( (а +в )с=а с вс); 4)Если скалярное пр-е равно 0, то либо равен 0 один из перемножаемых векторов, любо Cos угла между ними, т.е. векторы перпендикулярны. Скалярное произведение само на себя равно квадрату его модуля

7.Теорема о разложении вектора по базису. Ортонормированный базис.

Любой вектор системы может быть разложен по базису только единственным способом.

Доказательство:

Пусть есть система векторов и , которое является базисом системы

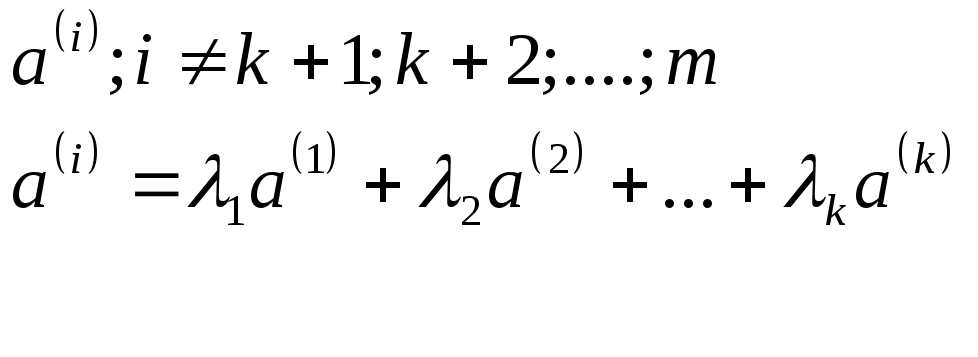
Предполагаем

Рассмотрим вектор:

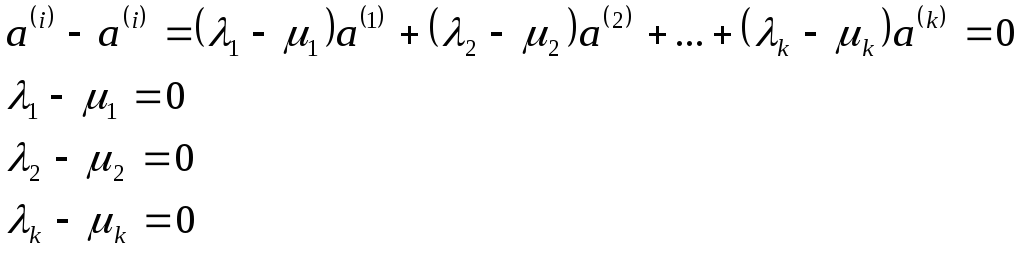
Двух различных разложений быть не может.

8. Матрицы. 9.Операции над матрицами.

Матрицей размера mxn называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Вектор-строкой называют матрицу, состоящую из одной строки. Вектор-столбцом - из одного столбца. Матрица, у которой количество столбцов равно количеству строк, называется квадратной матрицей n-ого порядка. Элементы матрицы, у которых номер строки и номер столбца совпадает, называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы матрицы равны нулю, то матрицу называют диагональной. Если у диагональной матрицы n-ого порядка на главной диагонали все элементы равны 1, то матрица называется единичной и обозначается Е. Матрица любого размера, все элементы которой равны 0, называется нуль-матрицей.

9 билет Умножение матрицы на число: условий нет, умножить на число можно любую матрицу. Произведением матрицы А на число  называется матрица В, равная А, каждый элемент которой находится по формуле: b_ij = x a_ij. Для того, чтобы умножить матрицу на число необходимо умножить на это число каждый элемент матрицы. 2)Сложение 2-х матриц: условие - складывать можно только матрицы одинакового размера. Суммой 2-х матриц А и В называется матрица С=А+В, каждый элемент которой находится по формуле С_ij=a_ij+b_ij. Для того, чтобы сложить 2 матрицы, необходимо складывать между собой элементы, стоящие на одинаковых местах. 3)Вычитание 2-х матриц: операция аналогична сложению.

Билет 10 Умножение 2-х матриц: умножение А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произведением матрицы А размера mxk на матрицу В размера kxn называется матрица С размера mxn, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В. 5)Возведение в степень: возводить в степень можно только квадратные матрицы; целой положительной степенью квадратной матрицы А^m называется произведение m-матриц, равных А. 6)Транспонирование: условий нет; транспонирование-операция, в результате которой строчки и столбцы матрицы меняются местами с сохранением порядка элемента, при этом элементы главной диагонали остаются на своих местах.

9.Системы линейных алгебраических уравнений. Матричная форма записи. Линейным уравнением относительно неизвестных x₁,x₂,…,x_n называется выражение вида a₁x₁+a₂x₂+…+a_nx_n=b, где a₁,a₂,…,a_n и b- простые числа, причём a₁,a₁,…,a_n называются коэффициентами при неизвестных, а b- свободным коэффициентом. Последовательность чисел k₁,k₂,…,k_n называется решением уравнения, если при подстановке этих чисел в уравнение оно обращается в верное равенство. Два линейных уравнения называются равносильными, если их решения совпадают. Чтобы получить равносильное уравнение из заданного, необходимо осуществить следующие преобразования: 1) перенос слагаемых из одной части уравнения в другую; 2) поэлементное умножение всего уравнения на одно и то же число, отличное от ноля. Решить линейное уравнение – это значит найти все его решения или установить, что их нет. Система уравнений называется совместной, если она имеет хотя бы одно решение. Система уравнений называется определённой, если она имеет одно единственное решение, и неопределённой, если решений множество. Неизвестное x₁ называется разрешённым, если к.-н. уравнение системы содержит неизвестное x₁ с коэффициентом, равным 1, а во все другие уравнения системы неизвестное x₁ не входит. Если каждое уравнение системы содержит разрешённое неизвестное, то такую систему называют разрешённой. Неизвестные СЛАУ, которые не входят в разрешённый набор, называются свободными. Разрешённая СЛУ всегда совместна, она будет определённой, если число ур-ий равно числу неизвестных; и неопределённой, если число неизвестных больше, чем ур-ий. Для того, чтобы определить совместна система или нет, не решая её, можно воспользоваться теоремой Кронекера-Капелли. Матрица, эл-тами которой являются коэффициенты при неизвестных системы, называется матрицей системы. Матрица системы, дополненная столбцом свободных коэффициентов, называется расширенной матрицей. Правило Крамера: пусть А-определитель матрицы системы, а j-определитель матрицы, полученной из матрицы системы заменой j-ого столбца на столбец свободных коэффициентов; тогда, если А0, то система имеет единственное решение, определяемое по формуле  Xj= j/ A. Противоречивым называется ур-е вида OX₁+OX₂+...+OX_n=b. Если каждое ур-е системы содержит разрешённое неизвестное, то такую систему называют разрешённой. Неизвестное x₁ называют разрешённым, если к.-н. ур-е системы содержит неизвестное x₁ с коэффициентом, равным 1, а во все другие ур-я системы неизвестное x₁ не входит.

10 билет. Умножение матриц А и В определено, если число столбцов первой матрицы = числу строк второй матрицы. Тогда произведением матриц и называется такая матрица , каждый элемент которой равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В.

Отличие умножения матриц от умножения числа.

А) АВВА

Произведение матриц не будет существовать (при перестановке матриц), тк число столбцов 1й матрицы не будет совпадать с числом столбцов 2й матрицы.

Б) если произведение существует, то матрицы могут быть разных размеров.

В) если оба произведения АВ и ВА существуют и оба – матрицы одинакового размера, переместительный (коммутативный) закон умножения не выполняется, т.е. АВВА. Например: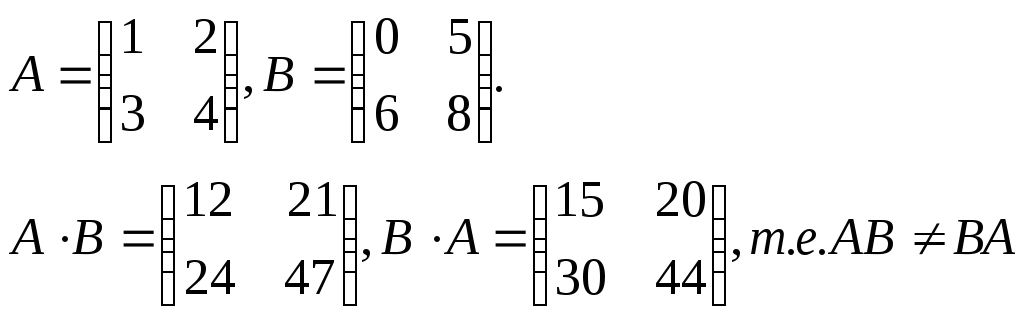

Г) Произведение двух ненулевых матриц может ровняться нулевой матрице, т.е. из того, что А*В=0, не следует, что А=0, или В=0. Например,

11. Ранг матрицы. Рангом матрицы А называется наивысший порядок отличных от 0 миноров этой матрицы rang A=r(A). Ранг матрицы не изменяется при проведении элементарных преобразований. Преобразования: 1)отбрасывание строки или столбца, состоящих из одних нулей; 2)умножение всех эл-ов к.-л. строки или столбца матрицы на одно и то же число, отличное от 0; 3)изменение порядка строк или столбцов матрицы; 4)прибавление к каждому эл-ту к.-л. строки или столбца эл-ов др. строки или столбца, умноженных на одно и то же число, не равное 0; 5) транспонирование матрицы.

Билет №12

Пусть матр. А-квадр., тогда каждой квадр. матр. можно поставить в соответствие некотор. число, котор. назыв. определителем матр.

Определит.матр. 1-го порядка |а|-это само число=а

Определитель 2-го порядка число = (из произведений элементов главной диагонали вычитается произведение элементов второй диагонали матрицы А.)

Определитель 3-го порядка:

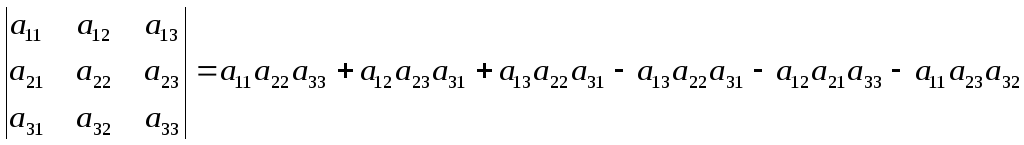
Правило треугольников(прав.Сарусса):

Билет №13Рассмотр.квадр.матр. n-го порядка: 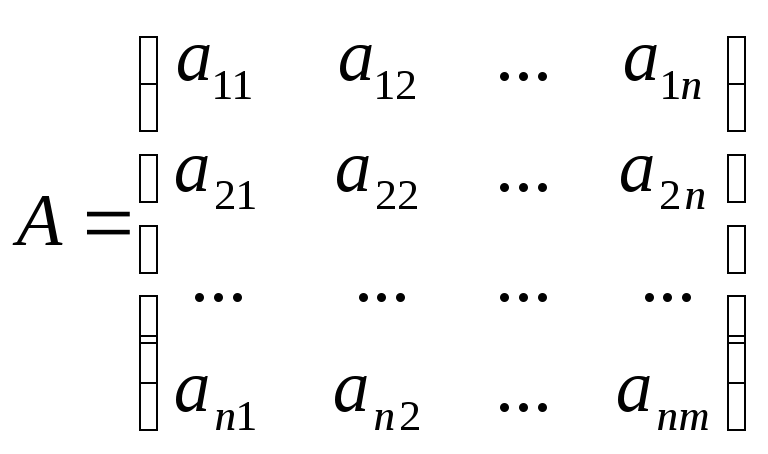. Из общего числа элементов этой матр.выберем набор, содерж. n элем.,т.о., чтобы в него входило по одному элем. Из кажд.строки и кажд.столца. Люб.такой набор можно упорядочить, записав сначала элем.из 1-ой строки, затем из 2-ой и т.д.,т.е:. Номера столбцов образуют при этом перестановку J из n чисел: 1,2,…,n. Всего сущ. n! Различ.перестановок из n натур.чисел. Беспорядок(инверсия) в перестановке J-это наличие пары чисел, в котор. большее число предшествует меньшему. Обзнач.через r(J) кол-во инверсий в перестановке J. Кажд.набору из элем.матр. А можно постав.в соответствие произведен.его элем.: и число r(J), равное кол-ву инверсий в перестановке из номеров соответсв.столбцов.

Определен.: Определителем квадратной матрицы n-го порядка (определителем n-го порядка) назыв.число, равное алгебраич.сумме n! Членов, кажд. Из котор. является произведен. n элем.матр., взятых по одному из кажд.строки и кажд.столбца, причем знак кажд.члена определяется как , где r(J)-число инверсий в перестановке J из номеров столбцов элем.матр., если при этом номера строк записаны в порядке возрастания: 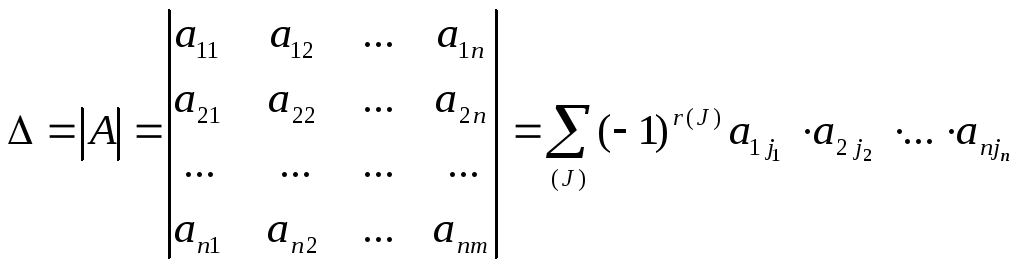, где сумма берется по всем перестановкам J. Важное значен. Для вычислен.определителей имеет следующая теорема. Теорема Лапласа: Определитель квадрат.матр. равен сумме произведений элем.люб.строки (столбца) на их алгебраические дополнения: (разложен. По элем. i-й строки; ); (разложен. По элем. j-го столбца; )

14.Минор и алгебраическое дополнение

Минором М_ij квадратной матрицы n-го порядка для элемента а_ij называется определитель (n-1)-ого порядка, полученный с данного вычёркиванием i-ой строки и j-ого столбца. Алгебраическим дополнением А_ij для элемента квадратной матрицы а_ij называется минор этого элемента, взятый со знаком (-1)^i+j .

15. Свойства определителей.

1) Если к.-л. строка или столбец в матрице состоит из одних нолей, то (определитель) этой матрицы равен 0. 2)При транспонировании матрицы её определитель не изменяется: А = А’ . 3) Если все элементы к.-л. строки или столбца матрицы умножить на одно и то же число, то и  этой матрицы умножится на это же число. 4) При перестановке местами 2-х строк или столбцов матрицы её определитель меняет свой знак на противоположный. 5) Если квадратная матрица содержит 2 одинаковых строки или столбца, то её определитель равен 0. 6)Если 2 строки или 2 столбца матрицы пропорциональны, то её  равен 0. 7) Сумма произведений элементов к.-л. строки или столбца матрицы и другой строки или столбца равна 0. 8) Определитель матрицы не изменяется если к элементам одной строки или столбца прибавить элементы другой строки или столбца, умноженный на одно и то же число. 9)Если к.-л. столбец или строка матрицы представляет собой сумму 2-х элементов, то  этой матрицы может быть представлен в виде суммы 2-х определителей.10)Определитель произведения двух квадратных матриц равен произведению их определителей.

16. Обратная матрица.

Матрица А-1 называется обратной по отношению к квадратной матрице А, если при умножении её на заданную как справа так и слева получатся единичная матрица. Теорема (необходимое и достаточн.условие сущ-я обратн.матрицы): обратная матрица А-1 сущ-т и единственна тогда и только тогда, когда заданная матрица не вырожденная.Алгоритм вычисления обратной матрицы: 1)находим определитель исходной матрицы.если \А\не равно 0,то переходим к след. Этапу.2)Находим матрицу Ат,транспонированную к А 3)Находим алгебраическое дополнение транспонированной матрицы и составляем из них присоедин матр.А 4)Вычисляем обратную матр по формуле

17 билет. Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида a11x1 + a12x2 + … + a1nxn = b1,

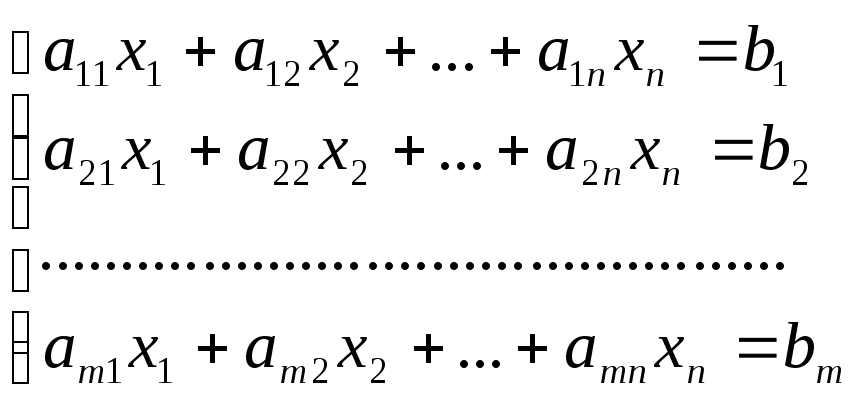
Система линейных алгебраических уравнений, содержащая уравнений и неизвестных имеет следующий вид: - столбец неизвестных, 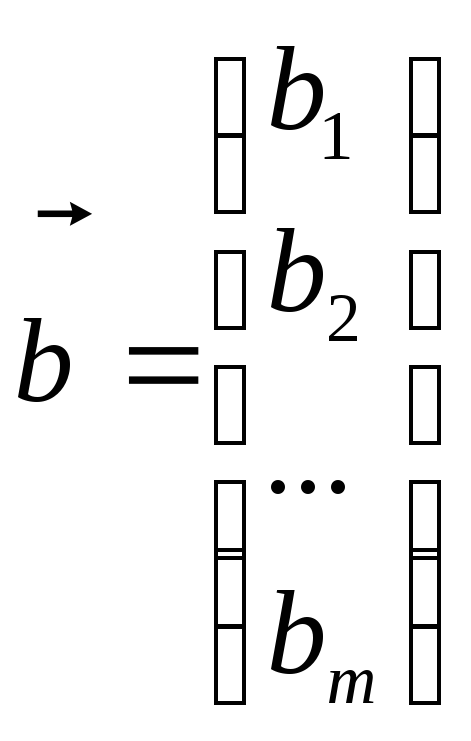- столбец свободных членов.,Матрицу 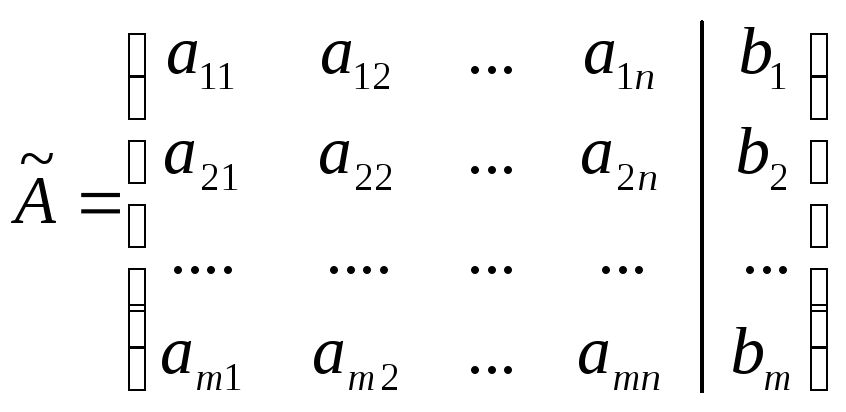- называют расширенной матрицей системы.

Определение. Система линейных алгебраических уравнений называется прямоугольной, если , и квадратной, если .Определение. Система линейных алгебраических уравнений называется однородной, если , т.е., если столбец свободных членов состоит из одних нулей. Определение. Система линейных алгебраических уравнений называется неоднородной, если .

Определение. Система линейных алгебраических уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Определение. Совместная система линейных алгебраических уравнений называется определенной, если она имеет только одно решение, и неопределенной, если она имеет более одного решения. Совместность системы может быть определена с помощью теоремы Кронекера-Капелли. Теорема. Для того , чтобы система была совместна, необходимо и достаточно, чтобы ранг матрицы системы равнялся рангу расширенной матрицы. Определение. Если ранг матрицы системы равен рангу расширенной матрицы, т.е. , то ранг матрицы системы называют рангом системы.

Замечание. Если ранг системы равен числу неизвестных, то система определённая.Теорема (Крамера). Если матрица квадратной системы невырожденная, то система определенная.В этом случае решение системы может быть найдено по формулам Крамера. Теорема. Если ранг однородной системы меньше числа неизвестных, то такая система имеет фундаментальную совокупность решений, состоящую из решений, где число неизвестных, ранг системы. Определение. Совокупность решений однородной системы называется фундаментальной, если выполняются два условия: 1) эта совокупность линейно независимая; 2) любое решение однородной системы может быть линейно выражено через эту совокупность.

Элементарные преобразования системы линейных уравнений.

К ним относятся - перестановка любых двух уравнений; - умножение обеих частей одного уравнения на любое число отличное от нуля; - прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число. Элементарные преобразования переводят данную систему в эквивалентную.

Метод Гаусса решения системы линейных уравнений состоит в том, что с помощью элементарных преобразований последовательно исключаются неизвестные, и данная система превращается в ступенчатую. Приводить к ступенчатому виду удобнее не саму систему, а её расширенную матрицу, выполняя все преобразования над её строками. Формулы Крамера. Решение неоднородной системы уравнений с неизвестными, имеющей невырожденную основную матрицу системы, находится по формулам

, где - определитель системы; - определитель матрицы, получаемой из основной матрицы системы заменой её -го столбца столбцом свободных членов

18билет. чтобы решить слау матричным методом, надо применить метод обрат матрицы

Пусть матрица невырожденная, т.е. ее определитель

Тогда существует обратная матрица.

Умножим слева обе части матричного неравенства на матрицу . Получим

Т. к.

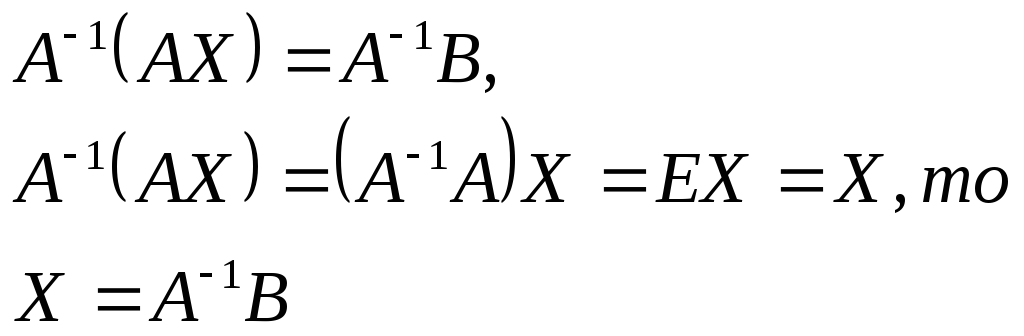
19. Правило Крамера: Пусть ∆- определитель матрицы системы А, а ∆(j)- определитель матрицы, полученный заменой j-ого столбца на столбец свободных переменных, тогда если ∆≠0, то система имеет единственное решение, равное отношению ∆(j) к ∆.(записать как дробь) Доказательство: Запишем решение системы в матричной форме: Х= произведению обратной матрицы на матрицу свободный переменных В. Запишем обратную матрицу, как произведение 1/∆, на присоединенную матрицу. Получается: Х=1/∆*A(с волной)*В. Запишем матрицу А с волной в расширенном виде. В первой строке будет А(1,1),А(2,1),А(3,1)….А(n,1). Во второй строке будет А(1,2),А(2,2),А(3,2)…..А(n,2). ………………………………... А(1,n),A(2,n),А(3,n)…..А(n,n) Где А- алгебраические дополнения транспонированной матрицы А. Записываем В в расширенном виде:b(1) b(2) … b(n) Перемножая, получаем: Первая строка: b1*A(1,1)+b2*A(2,1)+…….+b(n)*A(n,1) Вторая строка: b1*A(1,2)+b2*A(2,2)+…….+b(n)*A(n,2) ……………………………………………. b1*A(1, n)+b2*A(2, n)+……+b(n)*A(n, n) По свойству определителей b1*A(1,1)+b2*A(2,1)+…….+b(n)*A(n,1) есть определитель матрицы ∆(j), полученной путем замены j-ого столбца на столбец свободных переменных. Получается, что x=1/∆* ∆(j). Теорема доказана.

20. Решение систем линейных алгебраических ур-ий методом Гаусса.

Метод Гаусса: каждую СЛАУ при помощи конечного числа преобразований можно превратить в разрешённую системы ур-ий или в систему, содержащую противоречивое ур-е.

Метод Гаусса решения СЛАУ

1)

Две СЛАУ –эквивалентные если все решения одной системы являются решением др системы и наоборот. Каждой системе единственным образом соответствует расшир. матрице системы.

Эквивалентными преобразованиями расширенной матрицы системы называется:

1)Перестановка строк в системе

2)умножение какой либо строки на некоторое число.

3)Прибавление какой либо строки(2) ,соответственно элементов др строки,умноженное на некоторое число

4)Удаление нулевых строк.

2)

Эквивалентные преобразования расширенной матрицы системы приводят исходную систему в эквивалентную, т е не меняют решения системы.

an≠0 (предположим это) разделим первую строчку на an получим ……. И там идёт решение всё дальше…