Вопрос 66. Признаки экстремума функции.

Пусть функция y=f(x) определена на интервале (a,b).

Определение. Точка х₀ называется точкой максимума (минимума) функции, если в некоторой окрестности этой точки выполняется условие: ().

Значения функции в этих точках называются максимумом (минимумом) функции. Максимум и минимум ф-ии – экстремумы ф-ии.

Окрестность точки х₀ может быть весьма малой по своим линейным размерам. Поэтому экстремум ф-ии часто называют локальным экстремумом, а точки максимума/минимума ф-ии– точками локального максимума/минимума ф-ии.

На одном промежутке ф-ия может иметь несколько экстремумов ф-ии. Важно, что минимум в одной точке может оказаться больше максимума в другой. Наличие максимума/минимума в точке промежутка Х вовсе не означает, что в этой точке ф-ия f(x) принимает наибольшее/наим. значение на этом промежутке (не означает, что она имеет в этой точке глобальный максимум/минимум).

Знание и умение находить экстремумы ф-ии позволяют нам более точно рисовать графики (более качественно).

Необходимое условие экстремума функции. Если точка х₀ является точкой экстремума (локального максимума, минимума) функции, то производная ф-ии в этой точке либо равна нулю (f'(x₀)=0), либо её не существует. Та

Точки, в которых выполнено необходимое условие экстремума (производная = 0 или не сущ-ет), называется критическими точками (критические точки должны входить в область определения ф-ии). Т.е. если в какой-либо точке имеется экстремум, то эта точка критическая. НО критическая точка не обязательно будет являться точкой экстремума! Таким образом, для нахождения экстремума ф-ии необходимо знать достаточное условие экстремума.

Теорема 1. Первое достаточное условие экстремума.

Если при переходе через точку х₀ производная дифференцируемой ф-ии меняет свой знак с + на -, то точка х₀ есть точка максимума ф-ии (переход с острых углов наклона на тупые), а если с – на +, - то точка минимума (переход с тупых углов наклона на острые).

Если изменение знака производной не происходит, то экстремума нет.

Доказательство:

Пусть производная меняет знак с + на -, т.е. в некотором интервале (a; х₀) производная положительна (), а в некотором интервале (х₀; b) – отрицательна (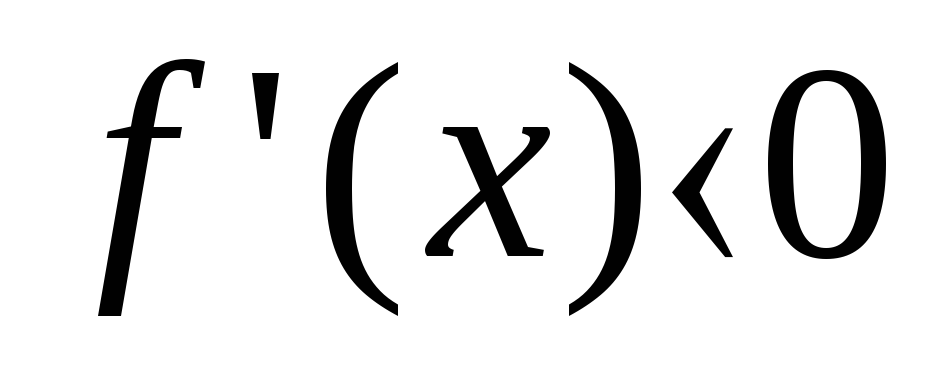). Тогда в соответствии с достаточным условием монотонности ф-ия возрастает на интервале (a; х₀) и убывает на инт. (х₀; b) (см. рис. ниже).

^а х₀ ^b

По определению возрастающей ф-ии при всех , а по определению убывающей ф-ии при всех , т.е. при всех , следоват., х₀ – точка максимума ф-ии . Теорема доказана.

Случай, когда производная меняет знак с – на +, рассматривается аналогично.

Теорема 2. Второе достаточное условие экстремума.

Если первая производная дважды дифференцируемой ф-ии = 0 в некоторой точке х₀, а вторая производная в этой точке положительна, то х₀ есть точка минимума ф-ии ; если отрицательна, то х₀ – точка максимума.

Доказательство:

Пусть = 0, а > 0. Это значит, что > 0 также и в некоторой окрестности точки х₀, т.е. возрастает на некотором интервале (a; b), содержащем точку х₀.

Но = 0, следоват., на интервале (a; х₀) < 0, а на инт. > 0, т.е. при переходе через точку х₀ меняет знак с – на +, т.е. х₀ – точка минимума.

Теорема доказана.

Случай, когда = 0 и < 0 рассматривается аналогично.

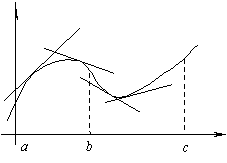
67.График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).

Примеры.

1. Полуокружность 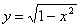выпукла на [–1; 1].

2. Парабола y = x² вогнута на интервале (-∞; +∞).

3. График функции в одних интервалах может быть выпуклым, а в других вогнутым. Так график функции y = sin x на [0,2; π], выпуклый в интервале (0; π) и вогнутый в (π; 2π).

4. Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.

Теорема. Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.

Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Определим достаточные условия того, что данная точка кривой является точкой перегиба.

Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x₀) = 0 или f ''(x₀) не существует и при переходе через значение x = x₀ производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x₀ есть точка перегиба.

Доказательство. Пусть f ''(x) < 0 при x < x₀ и f ''(x) > 0 при x > x₀. Тогда при x < x₀ кривая выпукла, а при x > x₀ – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x₀ есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x₀ и f ''(x) < 0 при x > x₀.

Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.

68.Асимптотой графика функции y=f(x) называется прямая,обладающая там свойствам,что расстояние от точки (х,f(х)) до этой прямой стремиться к нулю при не ограниченном удалении точки графика от начала координат.Для нахождения асимптот используют следующие теоремы. 1.    Пусть функция у= f(х) определена в некоторой окрестности точки х0 и хотя бы один из пределов функции равен бесконечности. Прямая х=х0 является вертикальной асимптотой графика функции у=f(х).Вертикальные асимптоты следуют искать в точках разрыва функции. 2.    Пусть функция у=f(х) определена при достаточно больших х и существует конечный предел.Тогда прямая у=b есть горизонтальная асимптота. 3.    Пусть функция у=f(х) определена при достаточно больших х и существует конечные пределы.Тогда прямая у=kx+b является наклонной асимптотой графика функции у=f(х).                       Общая схема исследования функций и построения графиков. 1)Найти область определения функции 2)Исследовать функцию на чётность и нечётность и периодичность. 3)Найти вертикальные асимптоты. 4)Исследовать поведение функции на бесконечностях и найти горизонтальные и наклонные асимптоты(если имеются). 5)Найти экстремумы и интервалы монотонности функции. 6)Найти интервалы выпуклости функции и точки перегиба. 7)Найти точки пересечения с осями координат. 69.Наибольшее и наименьшее значение функции на отрезке. Согласно теореме Вейерштрасса,если функция у=f(х) непрерывна на отрезке а, ,то она принимает на нём наименьшее значение.Наибольшее и наименьшее значение функции может достигаться как в точках экстремума,так и а точках на концах отрезка.   Для отыскания наибольшего и наименьшего значений на отрезке пользуются схемой: 1)    Найдите производную f’(х) 2)    Найдите критические точки функции,в которых f’(х)=0 или не существуют. 3)    Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее f и наименьшее f.