Вопросы: 1. Матрицы и действия над ними

Определения.

Матрицей называется прямоугольная  таблица чисел  или буквенных выражений, содержащая m строк и n столбцов:

,

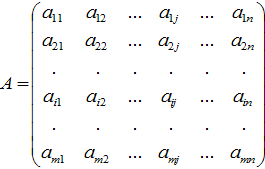  называют  элементами  матрицы.

Матрица, у которой число строк равно числу столбцов, т.е. m=n, называется квадратной матрицей, а число n называется порядком матрицы:

A =  

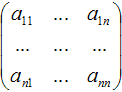
 Элементы   образуют главную диагональ квадратной матрицы. Если все элементы квадратной матрицы, расположенные вне главной диагонали, равны нулю, то матрицу называют диагональной. Если в диагональной матрице все элементы главной диагонали равны между собой, то ее называют скалярной.

Если в скалярной матрице все элементы главной диагонали равны единице, то матрицу называют единичной и обозначают буквой E .

Если все элементы матрицы  равны  0, то матрица называется нулевой и ее обозначают буквой O.

Две матрицы считаются равными, если они одинакового размера, и элементы, стоящие на пересечении строк и столбцов с одинаковыми номерами, равны, т.е. если

 

Сложение матриц.

Суммой матриц одной и той же размерности называется матрица размерности , каждый элемент которой представляет собой сумму соответствующих элементов матриц A и B:

Матрицы разных размерностей складывать нельзя.

Пример1. .

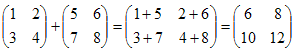Свойства сложения матриц. 1. Коммутативность. A+B=B+A 2. Ассоциативность. (A+B)+C=A+(B+C)

Умножение матриц, транспонирование матриц.

Матрица C, элементы которой с_ij равны элементам матрицы A, умноженным на число α, называют произведением матрицы A на α:

Пример 2. .

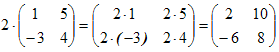Произведением матрицы размерности на матрицу размерности называется матрица размерности , где:

Произведение матриц существует только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример 3.

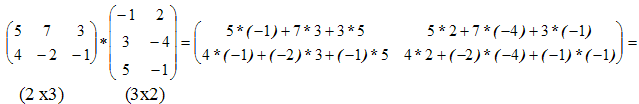
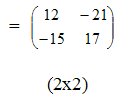
Пример 4.

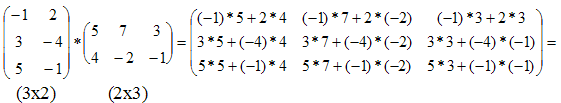
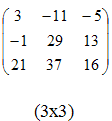
Результатом транспонирования матрицы размерности является матрица размерности , где

Пример 5.  

Свойства транспонированных матриц.

1). Если E-единичная матрица, то E=E^T.

2). Двукратное транспонирование не изменяет матрицу (A^T)^T=A.

3). Транспонирование суммы матриц равносильно сложению транспонированных матриц: (A+B)^T=A^T+B^T

4).Транспонирование произведения матриц равносильно умножению транспонированных матриц: .

5). Транспонирование обратной матрицы равносильно вычислению обратной к транспонированной матрице: (A^-1)^T=(A^T)^-1 .

6). Если транспонированная матрица A^T совпадает с данной матрицей A, то матрица A называется симметрической. 2. Алгебраическое дополнение и минор. Определитель матрицы

Определитель. Минор. Алгебраическое дополнение.

  Определителем второго порядка, соответствующим таблице элементов

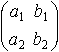
называется число a₁ b₂ - a₂ b₁. Определитель второго порядка обозначается так:

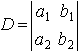
  Таким образом,

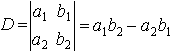
  Определитель третьего порядка, соответствующий таблице элементов

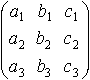
определяется равенством

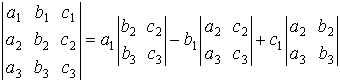
  Минором данного элемента определителя третьего порядка называется определитель второго порядка, который получится, если в исходном определителе вычеркнуть строку и столбец, содержащие данный элемент.   Алгебраическим дополнением данного элемента называется его минор, умноженный на ( - 1)^k, где k - сумма номеров строки и столбца, содержащих данный элемент.   Таким образом, знак, который при этом приписывается минору соответствущшего элемента определителя, определяется следующей таблицей:

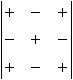
  В приведенном выше равенстве, выражающем определитель третьего порядка, в правой части стоит сумма произведений элементов первой строки определителя на их алгебраические дополнения.   Верна общая теорема: определитель третьего порядка равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения. Эта теорема позволяет вычислять значение определителя, раскрывая его по элементам любой его строки или столбца.   Отметим, что сумма произведений элементов какого-либо ряда на алгебраические дополнения элементов другого, но параллельного исходному ряда, всегда равна нулю.   Важнейшие свойства определителей второго и третьего порядков:   1) Определитель не изменится, если строки определителя заменить столбцами, а столбцы - соответствующими строками.   2) Общий множитель элементов какой-нибудь строки (или столбца) может быть вынесен за знак определителя.   3) Если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца) этого определителя, то определитель равен нулю.   4) При перестановке двух строк (столбцов) определителя знак этого определителя меняется на противоположный.   5) Определитель не изменится, если к элементам одной строки (столбца) определителя прибавить соответственные элементы другой строки (столбца), умноженные на одно и то же число (теорема о линейной комбинации параллельных рядов определителя).