Вопрос 21
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Пусть исходная система выглядит следующим образом
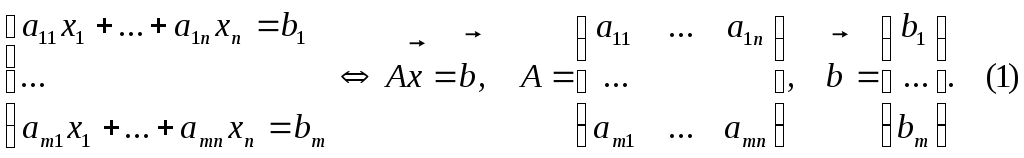
Тогда согласно свойству элементарных преобразований над строками эту систему можно привести к ступенчатому виду:
Переменные
называются
главными
переменными.
Все остальные называются свободными.
Если ,
то рассматриваемая система несовместна.
Предположим, что
.
Перенесём свободные
переменные за знаки равенств и поделим
каждое из уравнений системы на свой
коэффициент при самом левом x(,
Где i—
номер строки):
,где
.Если
свободным переменным системы (2) придавать
все возможные значения и вычислить
через них главные переменные, то мы
получим все решения этой СЛАУ.
Так как эта система получена путём
элементарных
преобразований
над исходной системой (1), то по теореме
об эквивалентности при элементарных
преобразованиях полученное нами решение
является решением системы (1).
22 билет.Системе m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены = 0.
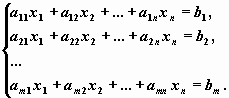
Система однородных уравнений всегда совместна, т. к. она всегда имеет, по крайней мере, нулевое (или тривиальное) решение (0; 0;…;0).
Система линейных однородных уравнений имеет ненулевые решения т. и т. т., когда ранг матрицы коэффициентов при переменных меньше числа переменных r(A)<n.
Обозначим решение
системы
в виде строки
.
-
Если строка
–
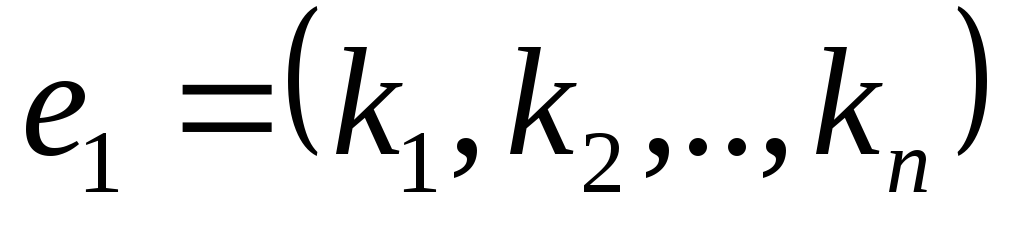решение системы, то и строка
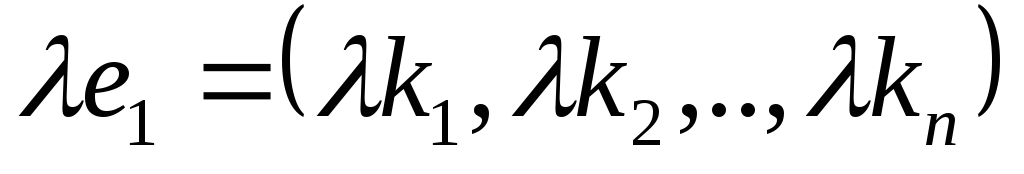также решение этой системы. -
Если строка
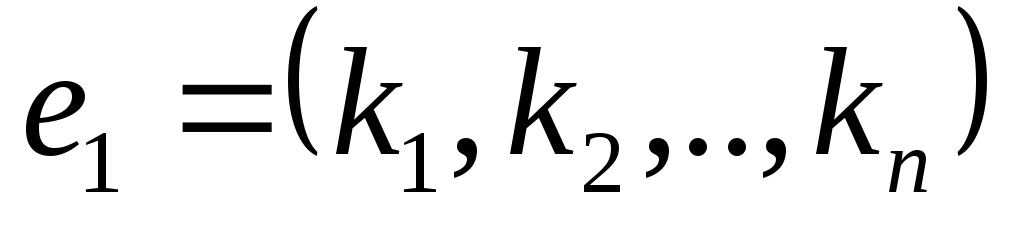и
–
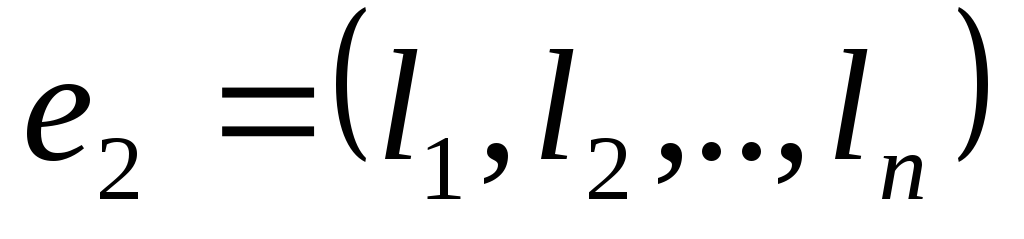решения системы, то при любых
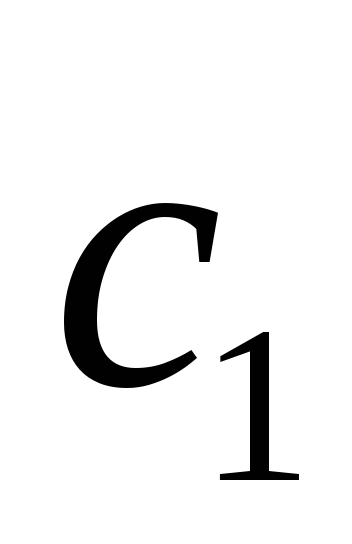и
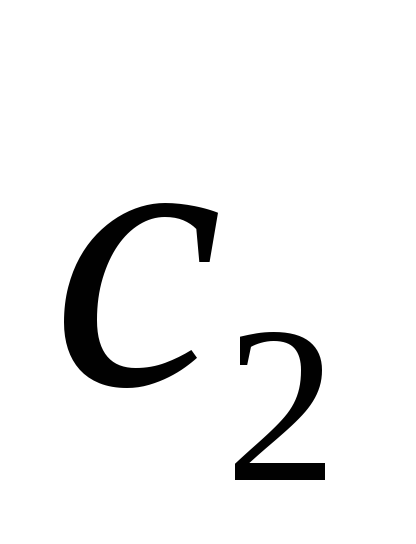их линейная комбинация
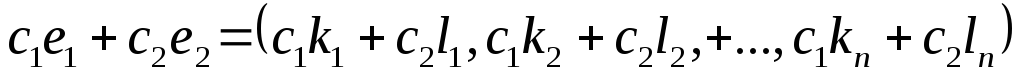также
решение данной системы.
Из свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы.
Система линейно
независимых решений
называется фундаментальной,
если каждое решение системы является
линейной комбинацией решений
.
Теорема. Если ранг матрицы коэффициентов при переменных системы линейных однородных уравнений меньше числа переменных н, то всякая фундаментальная система решений системы состоит из n-r решений.
Поэтому общее решение системы линейных однородных уравнений имеет вид
,
где
- любая фундаментальная система решений,
-
произвольные числа и k=n-r.
Можно сказать, что общее решение системы m линейных уравнений с n переменными равно сумме общего решения соответствующей ей системы однородных линейных уравнений и произвольного частного решения этой системы.
23//////////////
25 билет.Уравнение прямой на плоскости, различные его виды. Рассмотрим некоторую прямую в плоскости и вектор n(A,B), перпендикулярный этой прямой. Пусть есть точка на прямой М1(х1,у1) и произвольная точка М(х,у) на этой же прямой. Вектора М1М будет иметь координаты (х-х1,у-у1) Тогда т.к. прямая перпендикулярна данному вектору, а вектор принадлежит данной прямой, то вектор М1М будет перпендикулярен вектору n. Вектор n будет называться нормалью к вектору M1M. Скалярное произведение этих векторов будет равно: A(x-x1)+B(y-y1)=0(1) 1- уравнение прямой, проходящей через заданную точку, перпендикулярную заданному вектору. Раскроем скобки: Ax-Ax1+By-By1=0; Заменим -Ax1- By1=C Тогда уравнение примет вид: Ax+By+C=0(2) 2- общее уравнение прямой на плоскости. Выразим y через х получим: у= -A/B*x-C/B. Заменим -A/B=k, -C/B= b у=kx+b где k- tg угла наклона к положительной оси абсцисс, b-отрезок, который отсекает прямая от оси ординат или по-другому, смещение вдоль оси Оу. Возьмем на прямой точки M1(x1,y1), M2(x2,y2) и произвольную точку M(x,y). Векторы M1M(x-x1, y-y1), M1M2(x2-x1, y2-y1) будут коллинеарными, т.е. будет выполняться равенство: (x-x1)/(x2-x1)=(x2-x1)/(y2-y1). Пусть вектору M1M будет коллинеарен вектор d(m,n) Уравнение примет вид: (x-x1)/m=(y-y1)/n(3) 3-каноническое уравнение прямой. x/a+y/b=1(4) 4-уравнение прямой в отрезках, где а и b- отрезки, которые отсекает прямая от осей координат.