62. Теоремы Лагранжа и Коши.
Т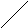
еорема
Лагранжа:
пусть функция f(х) непрерывна на отрезке
[a; b] и дифференцируема на интервале (a;
b), тогда внутри интервала существует
такая переменная
,
что
.Доказательство:Рассмотрим
вспомогательную функцию
Тогда посмотрим:
Ф-ия
непрерывна
на отрезке [a,b] и дифференцируема на
интервале (a,b) как сумма
,
т.е. эта функция удовлетворяет всем
условиям теоремы Роля
(
=существует)
,
такая, что
и
,
что и требовалось
доказать.
Отсюда еще утверждение теоремы, что
угловой коэф. касат. = угловому коэф.
секущей.
a
c
b
(дополнительное
определение:
теорема Ролля.
Пусть f(x) непрерывна на отрезке [a,b] и
дифференцируема на интервале (a,b) и пусть
на концах отрезка ф-ия принимает
одинаковые значения, поскольку она там
определена (f(a)=f(b)), тогда существует
переменная
такая, что
)).
Следствие
из теоремы:
(a<c<b)
формула
конечных приращений Лагранжа.
a<c<x
(c
– между a
и x!)
Теорема
Коши:
Пусть
функции f(x) и g(x)
непрерывны на отрезке [
]
и дифференцируемы на интервале (
),
причем
.
Тогда
(существует такая переменная с из
интервала (a; b) (с – между а и b!), что
…).Доказательство:
Покажем,
что если
,
то
.
Действительно,
для [
]
и g(x) выполнены условия теоремы Лагранжа.
,
и
Введем
в рассмотрение вспомогательную
функцию:
.
Покажем, что функция
удовлетворяет
всем условиям теоремы Ролля:
Ф-ия
непрерывна
на отрезке [
]
и дифференцируема на интервале (
)
как сумма
.
,
отсюда
.
Значит,
по теореме Ролля
такая, что
и
(делим на
)
- получили исходную формулу, что
и требовалось доказать.
Вопрос 63
Теорема Лопиталя: Предел отношений бесконечно малых и бесконечно больших функций равен пределу отношений производных, конечному или бесконечному, если последний существует в указном смысле.
Если имеется
неопределенность вида
или
,
то
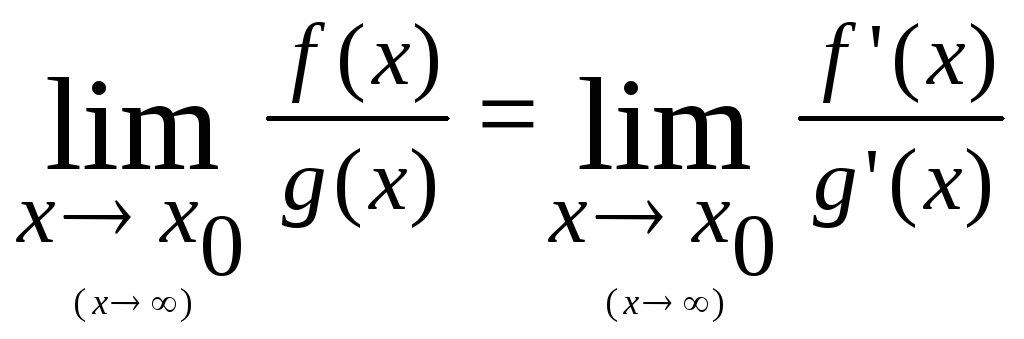
Рассмотрим
доказательство теоремы для неопределённости
вида
при
.
Для простоты будем
предлагать, что функции f(x)
и
g(x)
, а также их
производные непрерывны в точке
,
причём
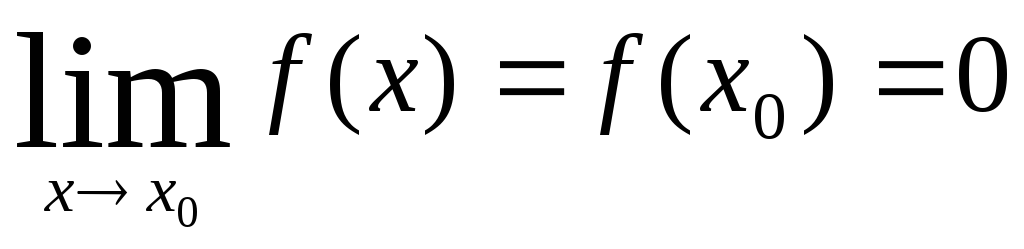и
.
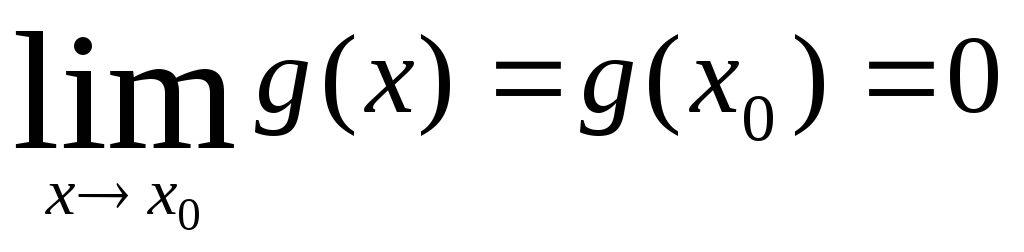В этом случае
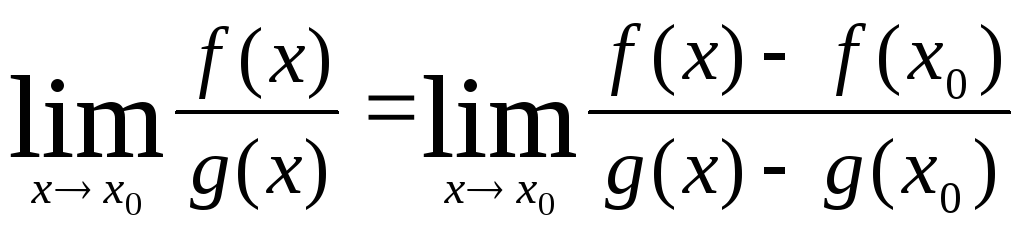
Применяя теорему
Лагранжа для функции f(x)
и g(x)
на отрезке
,
получим
,
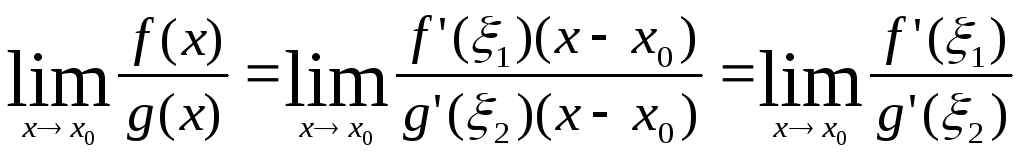где
.
При
в силу непрерывности производных f’(x)
и g’(x)
имеет
и
.
Используя теорему о пределе частного
двух функций, получим равенство
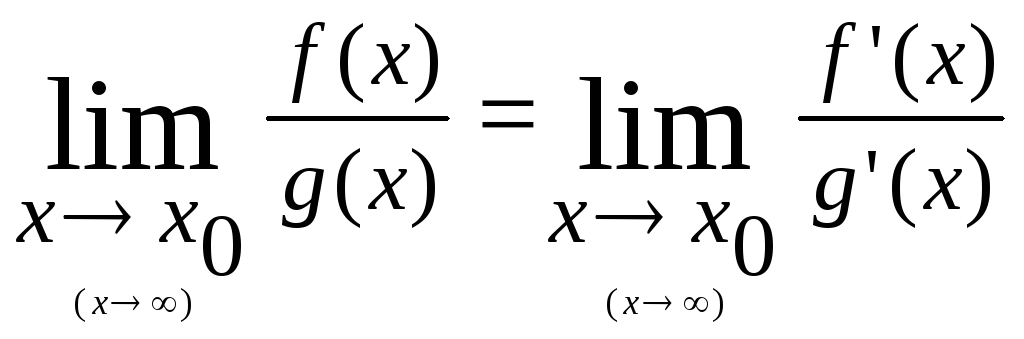
64.Формулы Тайлора и Маклорена Если функция f(x) имеет в точке а и некоторой её окрестности производные вплоть до (n+1)-го порядка,то для любого значения х из указанной области (х не=а).Формула Тайлора широко используется для приближённого вычисления значений функций вблизи точки а. Формула Маклорена является частным случаем формулы Тайлора для а=0.В частном случае,когда а=n – натуральное число,имеет место формула бинома Ньютона. Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.Если функция f(x) имеет в точке а и некоторой её окрестности производные вплоть до (n+1)-го порядка,то для любого значения х из указанной области (х не=а).Формула Тайлора широко используется для приближённого вычисления значений функций вблизи точки а. Формула Маклорена является частным случаем формулы Тайлора для а=0.В частном случае,когда а=n – натуральное число,имеет место формула бинома Ньютона.
Пусть функция f(x)
имеет n+1
производную в некоторой окрестности
точки a,
U(a,
).
Пусть
Пусть р – произвольное положительное число
Тогда
точка
при
x<a
или
при
x>a
65 вопрос. Признаки постоянства и монотонности функции. Функция y=f(x) называется возрастающей(убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее(меньшее) значение функции.
Пусть х1, х2
Х и х2 > х1. тогда функция возрастает на
промежутке Х, если f(х2)>
f(x1)
и убывает, если f(х2)<
f(x1).
Теорема. Для того чтобы функция f(x) была постоянна на интервале (а,b) нобходимо и достаточно, чтобы f’(x)=0.
Доказательство. Пусть производная равно 0 для любого Х из (a,b) , тогда f(x)=f(x0)+f’(x0)(x-x0)=f(x0)
Если функция постоянна то производная равна о.
Теорема. Для того,
чтобы f(x)
убывала(возрастала) на интервале (a,b)
необходимо и достаточно, чтобы f’(x0)
Доказательство. Возьмем х1, х2 из промежутка (a,b). х2 > х1.
Необходимость:
пусть f’(x0)
.
По теореме Лагранжа существует с
така что f’(с)
=
=
f’(c)(x2-x1)
f’(c)>0,
(x2-x1)>0,
следовательно
>0
т.е. функция возрастает.
Достаточность. Пусть функция возрастает. Тогда рассмотрим разность
>0.
перейдем к
