Существование

Чтобы найти обратную функцию, нужно решить уравнение x = F(y) относительно y. Если оно имеет более чем один корень, то функции обратной к F не существует. Таким образом, функцияf(x) обратима на интервале (a;b) тогда и только тогда, когда на этом интервале она инъективна.

Для непрерывной функции F(y) выразить y из уравнения x − F(y) = 0 возможно в том и только том случае, когда функция F(y) монотонна (см. теорема о неявной функции). Тем не менее, непрерывную функцию всегда можно обратить на промежутках её монотонности. Например,   является обратной функцией к x² на  , хотя на промежутке   обратная функция другая:  .

Свойства

• Областью определения F ^{− 1} является множество Y, а областью значений множество X.

• По построению имеем:

или

,

,

или короче

,

,

где   означает композицию функций, а id_X,id_Y — тождественные отображения на X и Y соответственно.

• Функция F является обратной к F ^{− 1}:

.

• Пусть 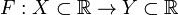  — биекция. Пусть 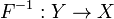  её обратная функция. Тогда графики функций y = F(x) и y = F ^{− 1}(x) симметричны относительно прямой y = x.

Сложная функция – функция от функции. Если z – функция от у, т.е. z(y), а у, в свою очередь, – функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.

В такой функции х – независимая, а у – промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).

Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:

.

Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов («цепное правило»): если z = f₁(y₁),y₁ = f₂(y₂), …, y_n-1 = f_n(x), то

9. Вопрос

Определение предела функции на языке окрестностей (различные случаи: в точке, на и на , конечный и неограниченный(бесконечный) пределы)

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а, также, описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).

10. Вопрос

Бесконечно малая функция. Свойства бесконечно малых функций.

БЕСКОНЕЧНО МАЛАЯ ФУНКЦИЯ - функция переменного х, к-рая при данном процессе изменения х становится и остается по абсолютной величине меньше любого заданного числа. Точнее, функция f(x), определенная в окрестности точки х₀, наз. бесконечно малой функцией при х, стремящемся к х₀, если для любого числа ε > 0 найдется такое число δ = δ (ε) > 0, что для всех х, удовлетворяющих условию |х - х₀ | < δ, выполняется |f(x)| < ε. Этот факт записывается так:

Символ

напр., означает, что для любого ε > 0 найдется такое N = N(ε) > 0, что для всех x > N выполняется неравенство |f(x)| < ε. Понятие Б. м. ф. может быть положено в основу общего определения предела функции. Именно, предел функции f(x) при х → х₀ конечен и равен А тогда и только тогда, когда

т. е. функция f(x) - А есть Б. м. ф.