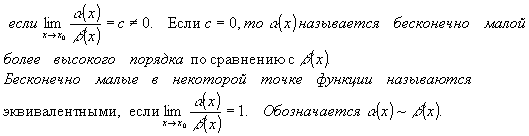Свойства:

1) Алгебраическая сумма любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

2) Произведение любого конечного числа бесконечно малых в некоторой точке функций есть функция, бесконечно малая в той же точке.

3) Произведение бесконечно малой в некоторой точке функции на функцию ограниченную есть функция, бесконечно малая в той же точке.

Бесконечно малые в некоторой точке х0 функции  (x) и  (x) называются бесконечно малыми одного порядка,

11. Вопрос

Теорема о связи функции и ее предела.

Теорема 1. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х).

▼ Пусть     

Следовательно, т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).▲  

Теорема 2. (обратная). Если функцию ƒ(х) можно представить в виде суммы числа А и бесконечно малой функции α(х), то число А является пределом функции ƒ(х), т. е. если ƒ(х)=А+α(х), то lim ƒ(х)=А при Х→Хо

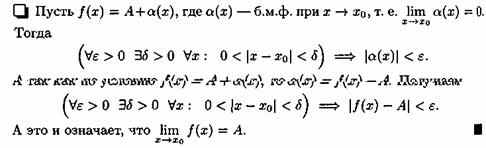
Пример:

Доказать, что

Решение: Функцию 5+х можно представить в виде суммы числа 7 и б.м.ф. х-2 (при х→2), т. е. выполнено равенство 5+х=7+(х-2). Следовательно, по теореме 17.6 получаем

Теорема о связи предела и бесконечно малой величины.

Если  , то  , где   – бесконечно малая величина. Или  .

Доказательство:

Допустим, что  , тогда  .

, значит  ,   – бесконечно малая величина.

Пример:

f(x) = x² + 1

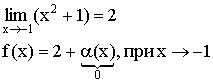
12. Вопрос

Определение бесконечно большой функции. Связь бесконечно малых и бесконечно больших функций.

Определение. Функция   называется бесконечно большой при  , если 

Лемма. Если   при  , то   при  , если   при  , то   при   и  .

БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ - функция переменного х, к-рая в данном процессе изменения х становится и остается по абсолютной величине больше любого наперед заданного числа. Точнее, функция f(x), определенная в окрестности точки х₀, наз. бесконечно большой функцией при х, стремящемся к x₀, если для любого числа М > 0 найдется такое число δ = δ (М) > 0, что для всех х ≠ х₀ и таких, что |х - х₀ | < δ, выполняется неравенство |f(x)| > M. Этот факт записывается так:

Аналогичным образом определяются

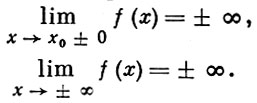
Напр.,

означает, что для любого М > 0 найдется такое δ = δ (M) > 0, что для всех z < - δ выполняется неравенство f(x) > M. Изучение Б. б. ф. может быть сведено к изучению бесконечно малых функций, т. к. если f(x) есть Б. б. ф., то функция ψ (х) = 1/f(x) является бесконечно малой.

Связь:

Между б.м. и б.б. функциями существует тесная связь.

Т: Функция, обратная к бесконечно малой, является б.б. и наоборот: — б.м., — б.б.,

13.Вопрос

Свойства пределов функций, связанные с арифметическими операциями над функциями.

14. Вопрос

Теорема о предельном переходе в неравенства.

Теорема 1. Если   и, начиная с некоторого номера, выполняется    , то    .

Доказательство. Пусть с некоторого номера выполняется  . Предположим, что  . Так как  , то для   существует такой номер N, что для всех   выполняется   или  , откуда получаем  , что противоречит условию. Случай   рассматривается аналогично.

Следствие 1. Пусть   и   сходятся и, начиная с некоторого номера, выполняется  , тогда  .

Следствие 2. Пусть   сходится и при любом    , тогда и  .

Доказательство. Так как  , то и  .

Теорема 2. Пусть   и с некоторого номера n выполняется условие  . Тогда последовательность   сходится и  .

Доказательство. Пусть   – номер, с которого выполняется  , тогда с этого номера выполняется  , или  . Так как   и  , то для любого числа   существуют такие номера   и  , что для всех    , а для всех    , а для всех номеров  , где   выполняется  , что и означает  .