
- •Характеристики систем автоматического управления и их звеньев.
- •Временные характеристики систем автоматического управления и их звеньев.
- •Характеристики интегрирующего звена.
- •Временные характеристики.
- •Частотные характеристики интегрирующего звена.
- •Апериодическое звено.
- •Правило построения логарифмической амплитудно-частотной характеристики апериодического звена.
- •Колебательное звено.
- •Характеристики колебательного звена.
- •Временные характеристики.
- •Частотные характеристики колебательного звена.
- •Логарифмическая амплитудно-частотная и фазо-частотная характеристики колебательного звена.
- •Дифференцирующее звено первого порядка.
- •Характеристики дифференцирующего звена первого порядка.
- •Временные характеристики.
- •Частотные характеристики.
- •Дифференцирующее звено второго порядка. Математические модели
- •Временные характеристики:
- •Частотные характеристики:
- •Логарифмические частотные
- •Правило построения асимптотических амплитудно-частотных характеристик разомкнутых систем автоматического управления.
- •Об устойчивости.
- •О переходном процессе.
- •О точности системы.
- •Точность систем автоматического управления при гармоническом входном воздействии.
- •Основные виды корректирующих устройств систем автоматического управления.
- •Последовательные корректирующие устройства.
- •Введение производной от ошибки.
- •Увеличение общего коэффициента усиления разомкнутой системы.
- •Введение интеграла от сигнала ошибки системы.
- •Изодромное корректирующее устройство.
- •Параллельные корректирующие устройства.
- •Положительная жесткая обратная связь.
- •Отрицательная жесткая обратная связь.
- •Инерционная жесткая обратная связь.
- •Гибкая обратная связь.
- •Инерционная гибкая обратная связь.
- •Корректирующие устройства по внешнему воздействию. Инвариантность.
- •Корректирующее устройство по задающему воздействию.
- •Корректирующее устройство по возмущению.
- •Краткое сравнение способов коррекции систем автоматического управления при помощи последовательных и параллельных корректирующих устройств.
- •Принцип дуальности управляемости и наблюдаемости.
- •В соответствии с последними уравнениями структурная схема системы имеет вид (сравнить с исходной структурной схемой).
- •Пусть заданна передаточная функция замкнутой системы
- •Или в векторно-матричной форме записи
- •Или в векторно-матричной форме записи
- •Уравнения (7)-(8), а, следовательно, и (9),(10), имеют каноническую форму записи, каноническая форма управляемости.
- •Пример. Задана желаемая передаточная функция разомкнутой системы ,
- •Решение. Желаемая передаточная функция замкнутой системы
- •Пример. Структурная схема объекта управления имеет вид, показанный на рисунке
- •Решение. Введем обозначения
Точность систем автоматического управления при гармоническом входном воздействии.
Пусть на вход системы автоматического управления поступает сигнал вида
![]() (1)
(1)
К такому виду сигналов могут быть приведены различные виды входных воздействий. Часто при проектировании систем автоматического управления задаются максимальные значения скорости и ускорения, которые должна отрабатывать автоматическая система.
В
этом случае по известным максимальным
скоростям и ускорениям входного
воздействия
![]() и
и![]() строят эквивалентное гармоническое
воздействие.
строят эквивалентное гармоническое
воздействие.
Здесь эквивалентность понимается в том смысле, что обеспечивается равенство максимальных значений скоростей и ускорений реального входного воздействия и эквивалентного синусоидального воздействия
![]() .
(2)
.
(2)
Каким
должно быть
![]() и
и![]() ,
чтобы
,
чтобы![]() имела максимальную скорость
имела максимальную скорость![]() и максимальное ускорение, равное
и максимальное ускорение, равное![]() .
.
Из (2) имеем
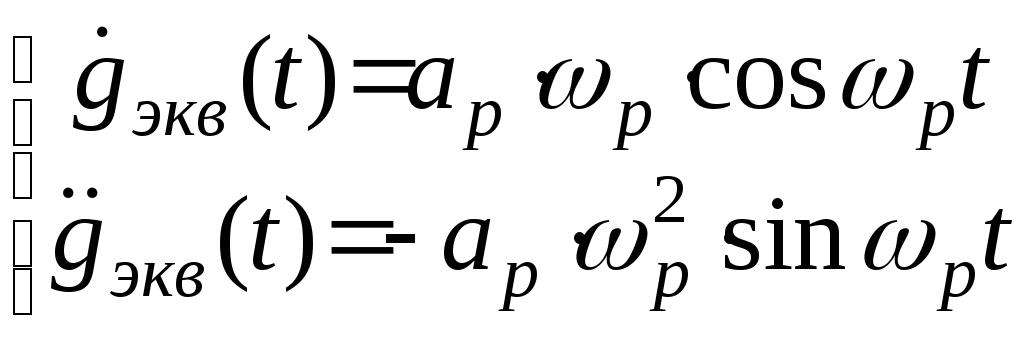 .
.
Откуда получаем
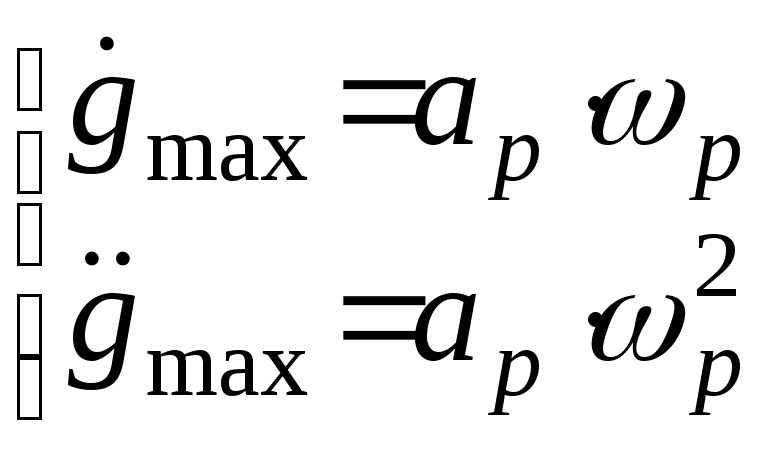 .
.
Из последних уравнений окончательно получаем
 ;
;
 . (3)
. (3)
Итак, будем считать, что структурная схема системы приведена к расчетной
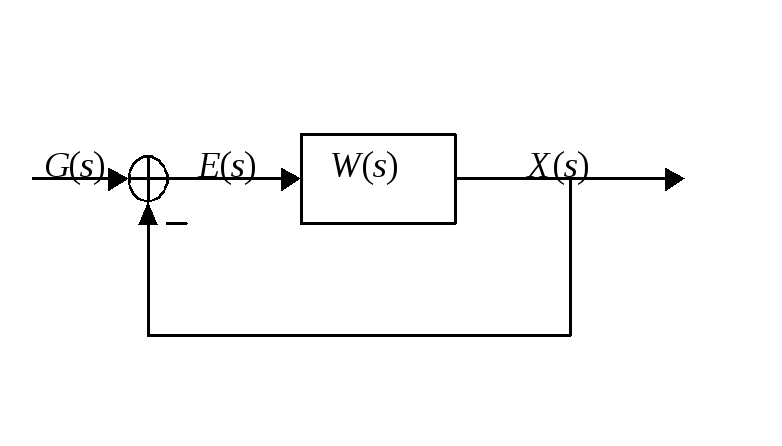
а
на вход системы подается входной сигнал
![]() ,
где
,
где
![]() и
и
![]() - рабочая амплитуда и частота входного
гармонического сигнала. В этом случае
амплитуда
- рабочая амплитуда и частота входного
гармонического сигнала. В этом случае
амплитуда![]() сигнала ошибки системы будет определяться
по формуле
сигнала ошибки системы будет определяться
по формуле![]() ,
или с учетом того, что
,
или с учетом того, что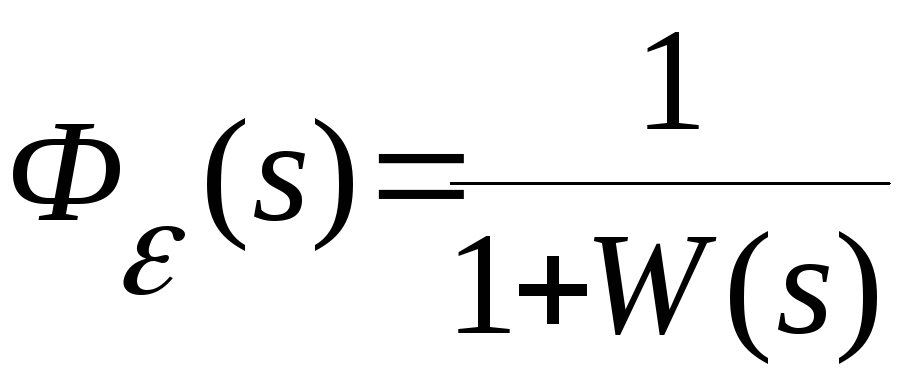 ,
значение
,
значение![]() будет равно
будет равно
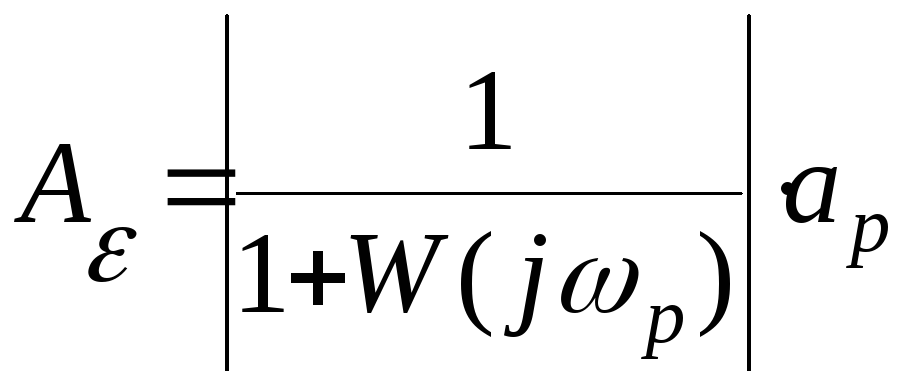 .
(4)
.
(4)
Если
рабочая частота
![]() такова, что справедливо неравенство
такова, что справедливо неравенство![]() ,
то равенство (4) можно заменить приближением
,
то равенство (4) можно заменить приближением
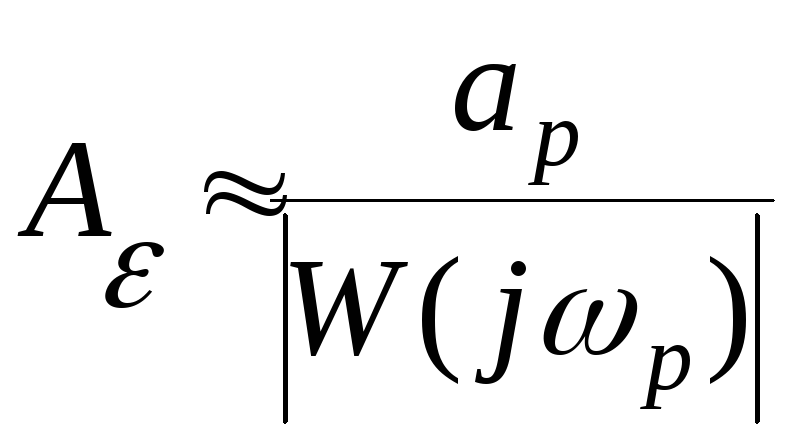 .
(5)
.
(5)
С помощью соотношений (4) и (5) можно оценить амплитуду ошибки отработки гармонического сигнала (1). Практическое значение приближенного равенства (5) состоит в том, что с его помощью и используя логарифмические амплитудно-частотные характеристики исследуемой системы, можно оценить максимальное значение ошибки в системе при гармоническом входном воздействии.
Пусть даны:
![]() -
амплитуда входного гармонического
сигнала;
-
амплитуда входного гармонического
сигнала;
![]() -
рабочая частота входного гармонического
сигнала.
-
рабочая частота входного гармонического
сигнала.
Логарифмическая
амплитудно-частотная характеристика
разомкнутой системы
![]() .
.
Требуется
определить
максимальное значение амплитуды ошибки
в замкнутой системы
![]() .
.
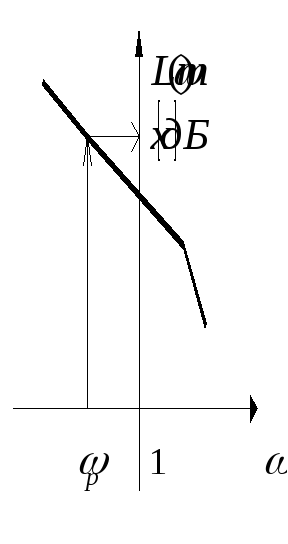
Для решения этой задачи необходимо:
На рабочей частоте
 по графику логарифмической
амплитудно-частотной характеристики
определяет значение
по графику логарифмической
амплитудно-частотной характеристики
определяет значение в дБ.
в дБ.Так как по определению логарифмической амплитудно-частотной характеристики
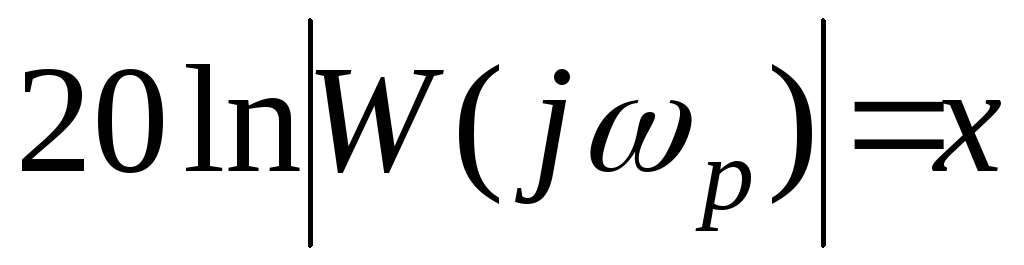 ,
то
,
то
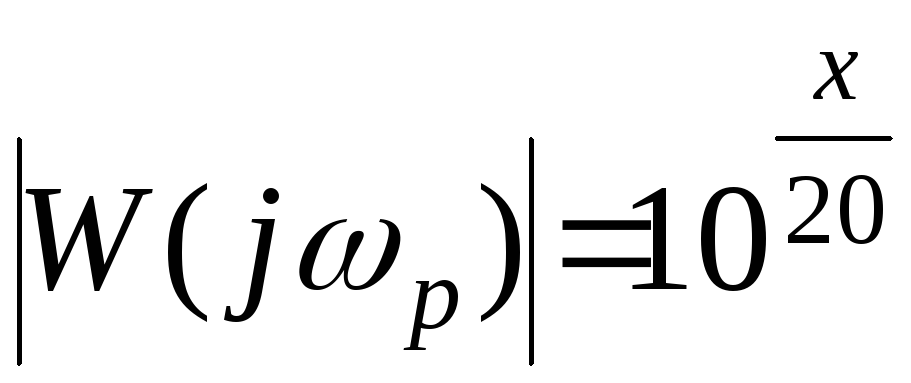 .
(6)
.
(6)
Подставив (6) в приближенное равенство (5) получаем то
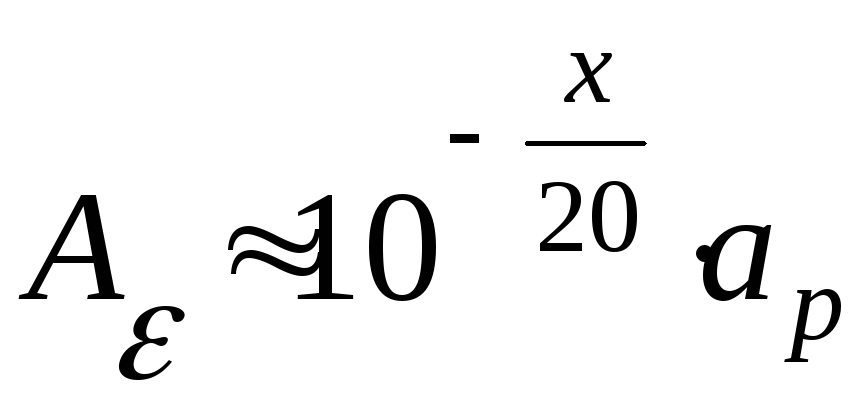 .
(7)
.
(7)
Пример. Задана система автоматического управления, структурная схема которой имеет
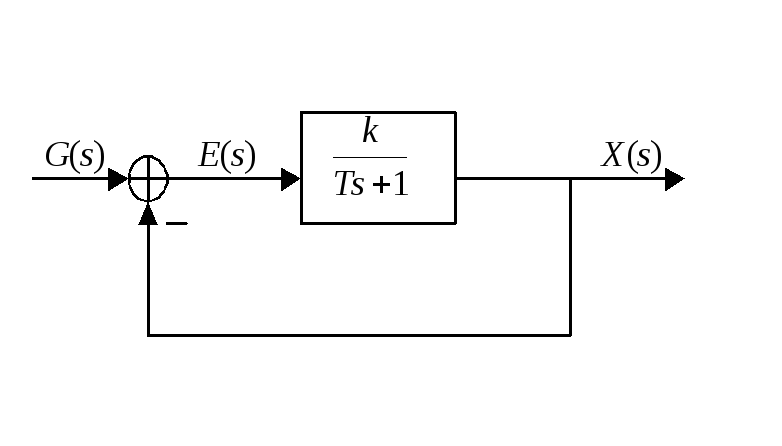
где
![]() ;
;![]() .
.
На
вход системы поступает входной
гармонический сигнал
![]() ,
где
,
где![]() - амплитуда;
- амплитуда;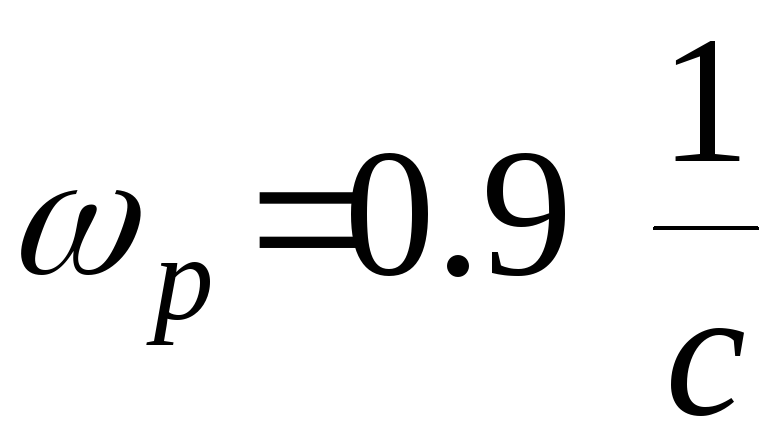 - частота входного сигнала.
- частота входного сигнала.
Найти амплитуду ошибки в заданной системе управления.
Решение. Передаточная функция разомкнутой системы
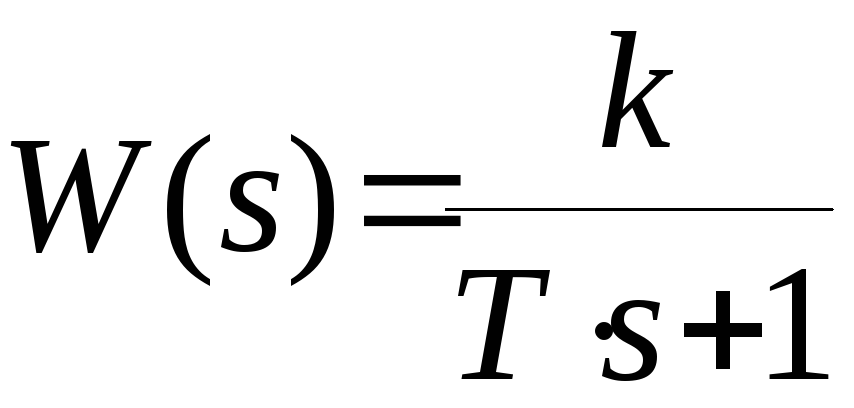 .
.
Передаточная функция замкнутой системы по ошибке
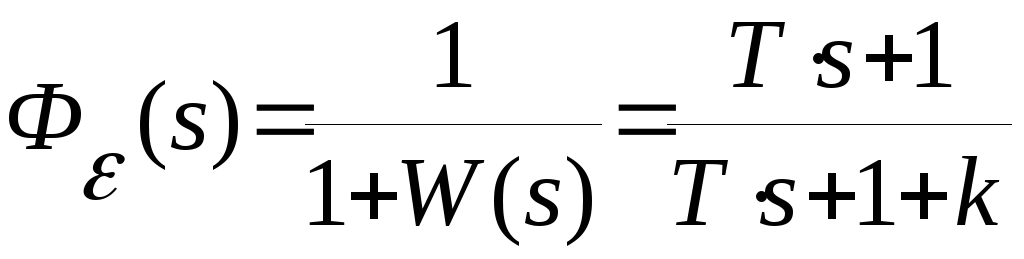
Из последнего равенства получаем

Для
заданных значений
![]() ,
,![]() и
и![]() получаем
получаем
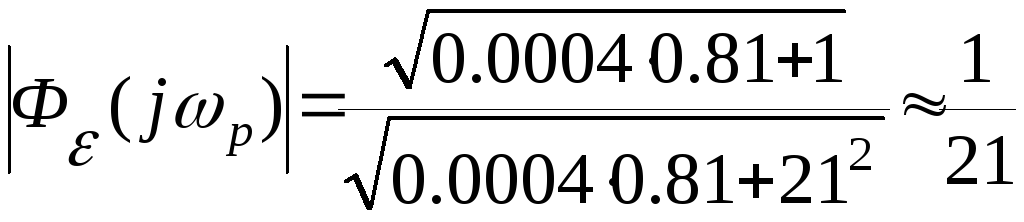
Поэтому искомое значение амплитуды ошибки
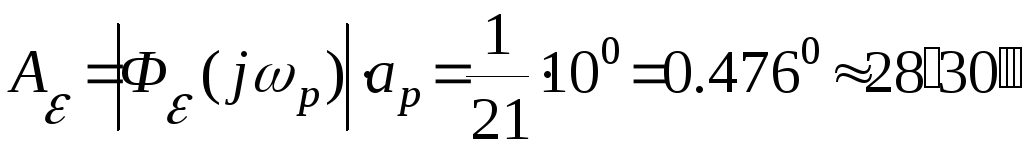
Вычислим
значение
![]() по приближенной формуле (5)
по приближенной формуле (5)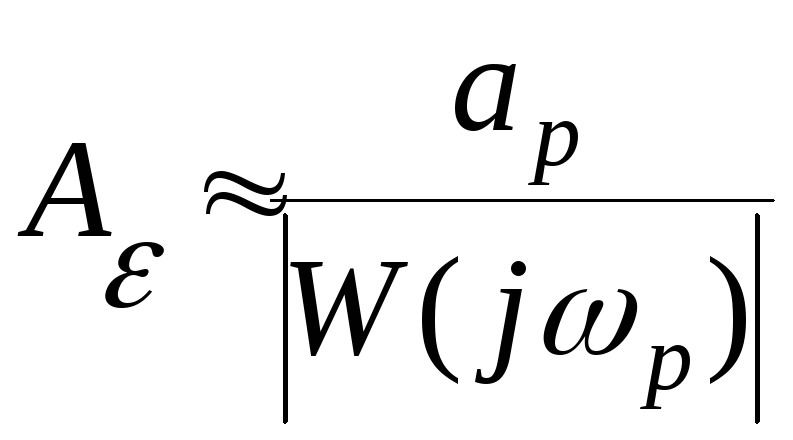 .
.
Из
передаточной функции разомкнутой
системы
![]() последовательно получаем
последовательно получаем
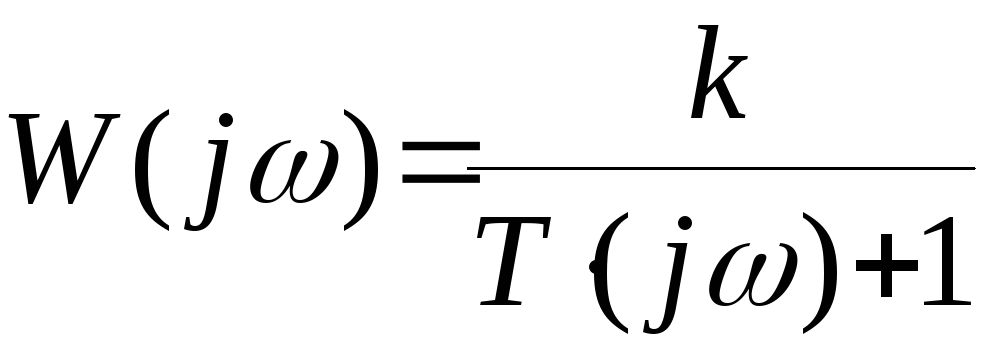 ;
;  .
.
Для заданных значений параметров имеем:
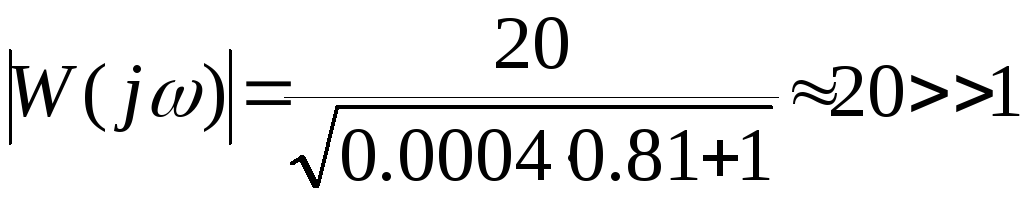 .
.
Поэтому, на основании приближенного равенства (5) получаем:
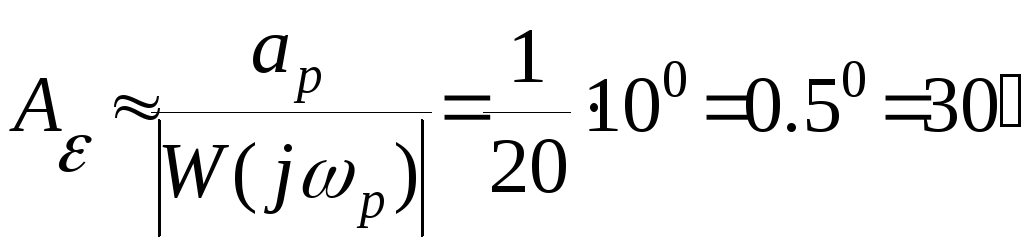 .
.
