
- •Характеристики систем автоматического управления и их звеньев.
- •Временные характеристики систем автоматического управления и их звеньев.
- •Характеристики интегрирующего звена.
- •Временные характеристики.
- •Частотные характеристики интегрирующего звена.
- •Апериодическое звено.
- •Правило построения логарифмической амплитудно-частотной характеристики апериодического звена.
- •Колебательное звено.
- •Характеристики колебательного звена.
- •Временные характеристики.
- •Частотные характеристики колебательного звена.
- •Логарифмическая амплитудно-частотная и фазо-частотная характеристики колебательного звена.
- •Дифференцирующее звено первого порядка.
- •Характеристики дифференцирующего звена первого порядка.
- •Временные характеристики.
- •Частотные характеристики.
- •Дифференцирующее звено второго порядка. Математические модели
- •Временные характеристики:
- •Частотные характеристики:
- •Логарифмические частотные
- •Правило построения асимптотических амплитудно-частотных характеристик разомкнутых систем автоматического управления.
- •Об устойчивости.
- •О переходном процессе.
- •О точности системы.
- •Точность систем автоматического управления при гармоническом входном воздействии.
- •Основные виды корректирующих устройств систем автоматического управления.
- •Последовательные корректирующие устройства.
- •Введение производной от ошибки.
- •Увеличение общего коэффициента усиления разомкнутой системы.
- •Введение интеграла от сигнала ошибки системы.
- •Изодромное корректирующее устройство.
- •Параллельные корректирующие устройства.
- •Положительная жесткая обратная связь.
- •Отрицательная жесткая обратная связь.
- •Инерционная жесткая обратная связь.
- •Гибкая обратная связь.
- •Инерционная гибкая обратная связь.
- •Корректирующие устройства по внешнему воздействию. Инвариантность.
- •Корректирующее устройство по задающему воздействию.
- •Корректирующее устройство по возмущению.
- •Краткое сравнение способов коррекции систем автоматического управления при помощи последовательных и параллельных корректирующих устройств.
- •Принцип дуальности управляемости и наблюдаемости.
- •В соответствии с последними уравнениями структурная схема системы имеет вид (сравнить с исходной структурной схемой).
- •Пусть заданна передаточная функция замкнутой системы
- •Или в векторно-матричной форме записи
- •Или в векторно-матричной форме записи
- •Уравнения (7)-(8), а, следовательно, и (9),(10), имеют каноническую форму записи, каноническая форма управляемости.
- •Пример. Задана желаемая передаточная функция разомкнутой системы ,
- •Решение. Желаемая передаточная функция замкнутой системы
- •Пример. Структурная схема объекта управления имеет вид, показанный на рисунке
- •Решение. Введем обозначения
Правило построения логарифмической амплитудно-частотной характеристики апериодического звена.
На оси частот отмечаем сопряжённую частоту
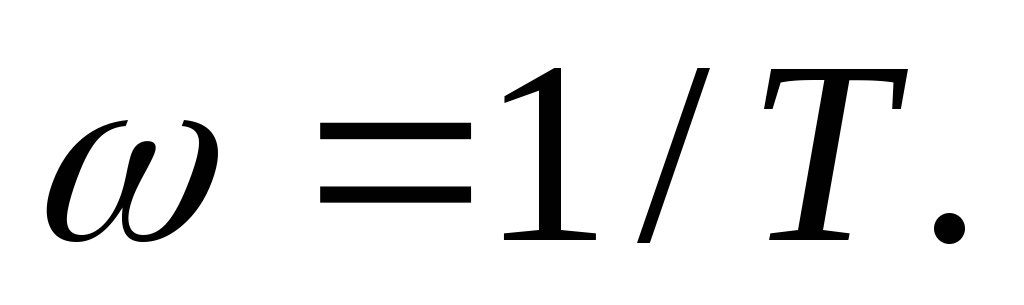
На оси ординат отмечаем точку
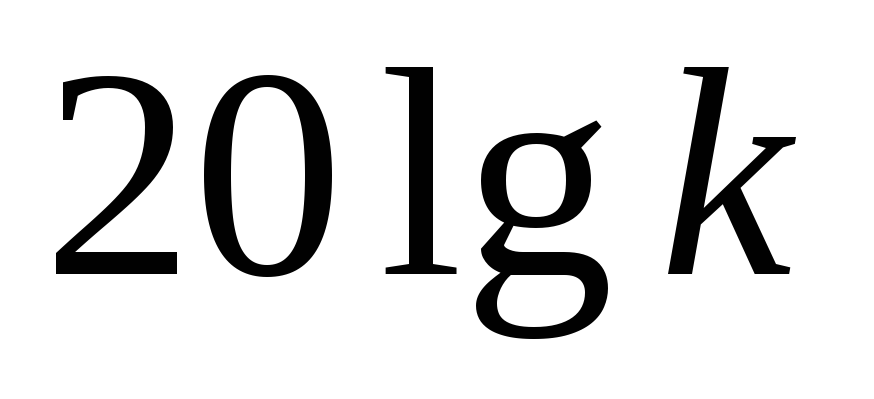 .
.Через точку на оси ординат, которая соответствует
 ,
проводят прямую, параллельную оси
частот до значения
,
проводят прямую, параллельную оси
частот до значения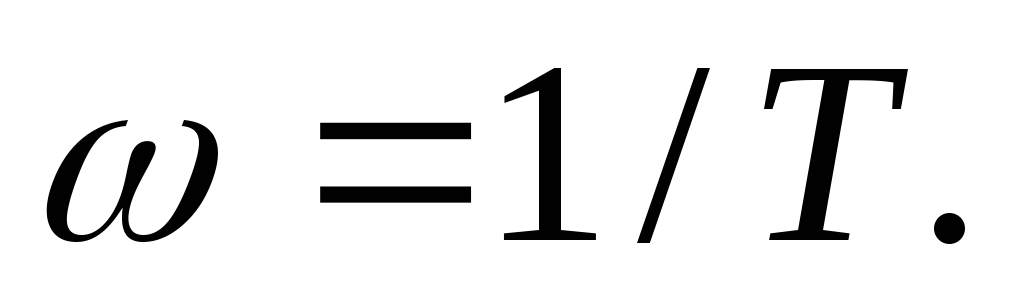
Через точку с координатами
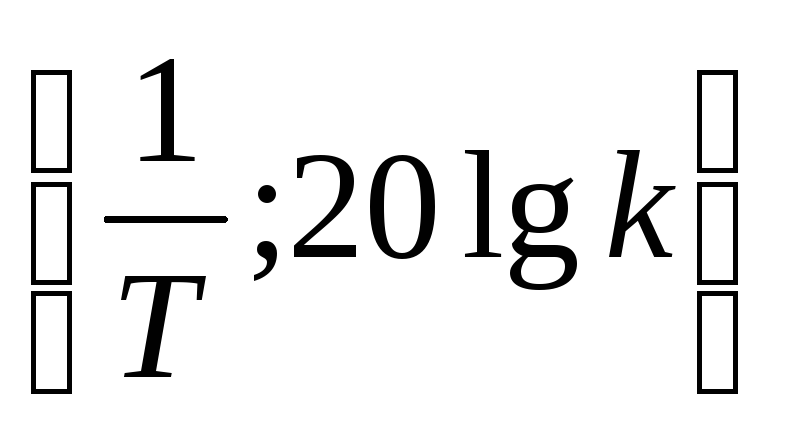 проводят
прямую с наклоном –20дБ. В результате
указанных построений получается
асимптотическая логарифмическая
амплитудно-частотная характеристика
апериодического звена.
проводят
прямую с наклоном –20дБ. В результате
указанных построений получается
асимптотическая логарифмическая
амплитудно-частотная характеристика
апериодического звена.Уточнение логарифмической амплитудно-частотной характеристики в окрестности сопрягающей частоты осуществляется с помощью шаблонов.
Колебательное звено.
Колебательным звеном называется простейший динамический элемент системы автоматического управления или его составная часть, имеющая передаточную функцию вида
![]() (1)
(1)
На структурных схемах колебательное звено изображается следующим образом:
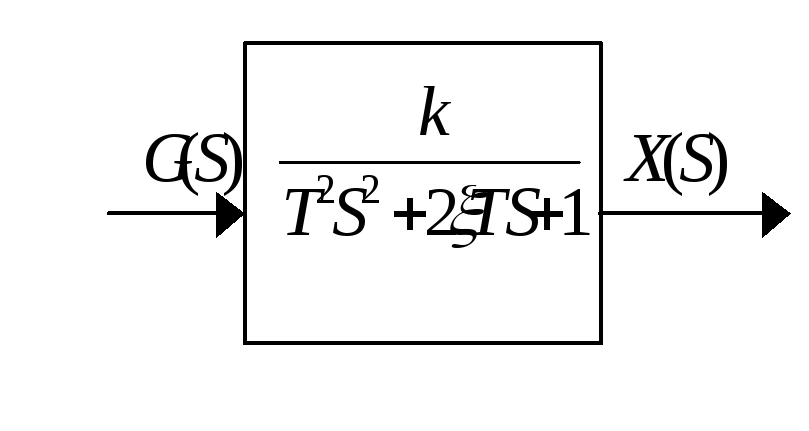
Динамические свойства колебательного звена определяются тремя параметрами
![]() -
коэффициентом усиления (передачи)
колебательного звена;
-
коэффициентом усиления (передачи)
колебательного звена;
![]() -
постоянная времени колебательного
звена;
-
постоянная времени колебательного
звена;
![]() -
относительный коэффициент затухания
колебательного звена
-
относительный коэффициент затухания
колебательного звена
![]() .
.
Замечание
Простейшую
дробь вида
![]() можно преобразовать к виду (1) следующим
образом:
можно преобразовать к виду (1) следующим
образом:
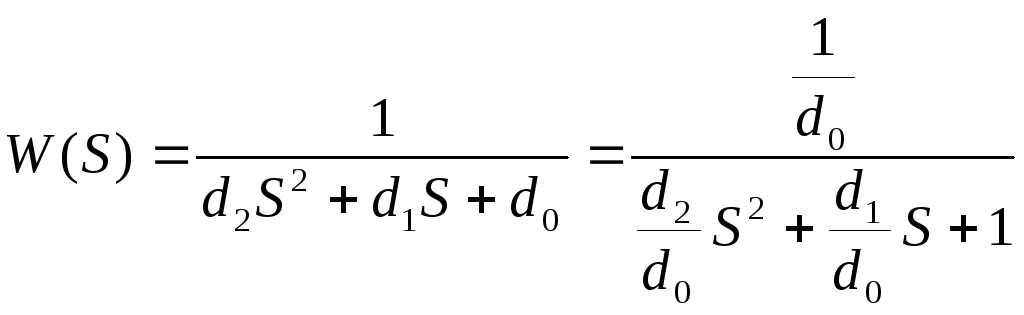 ;
;
Введём обозначения:
![]()
![]()
![]()
![]() ;
;![]()
Тогда последнее равенство принимает вид (1). Получим математическую модель колебательного звена в виде дифференциального уравнения:
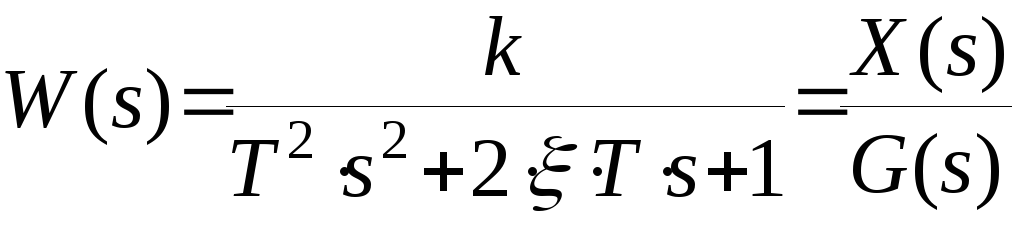 ;
;
![]() ;
;
 .
(2)
.
(2)
Это линейное дифференциальное уравнение второго порядка с постоянными коэффициентами. Следовательно, математической моделью колебательного звена является дифференциальное уравнение второго порядка с постоянными коэффициентами. Дифференциальному уравнению (2) соответствует характеристическое уравнение
![]() (3)
(3)
(сравним со знаменателем передаточной функции (1)), его корни вычисляются по формулам
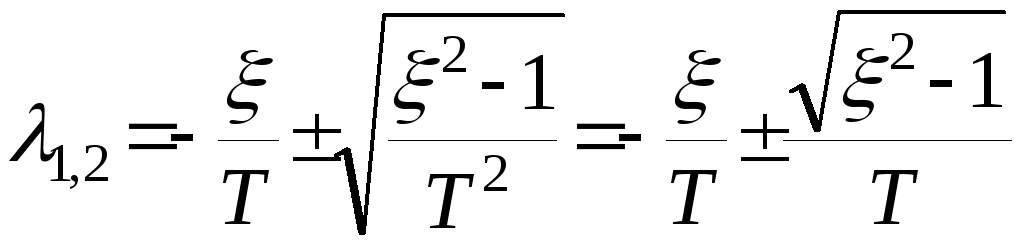 .
.
Так
как
![]() ,
то корни характеристического уравнения
(3) – комплексно-сопряжённые:
,
то корни характеристического уравнения
(3) – комплексно-сопряжённые:
![]() ;
;
![]() . (4)
. (4)
где
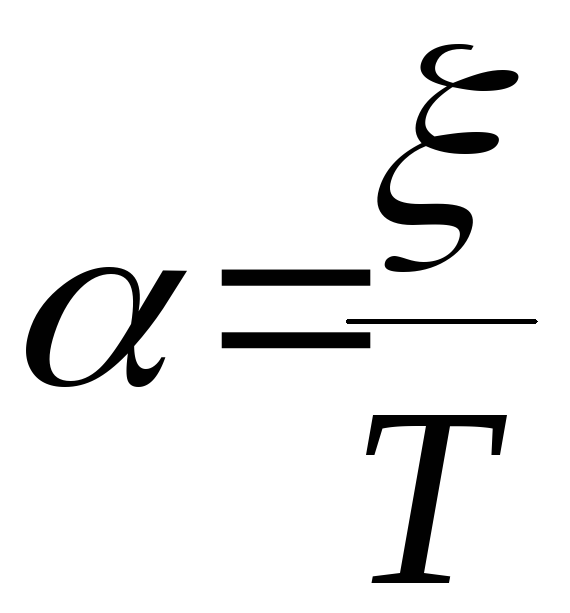 ;
;
 .
.
Таким
образом, общее решение однородного
дифференциального уравнения (![]() )
определяющее собственно динамические
свойства колебательного звена имеет
вид
)
определяющее собственно динамические
свойства колебательного звена имеет
вид
![]() ,
(5)
,
(5)
где
![]() и
и![]() – постоянные интегрирования.
– постоянные интегрирования.
Замечания.
Если
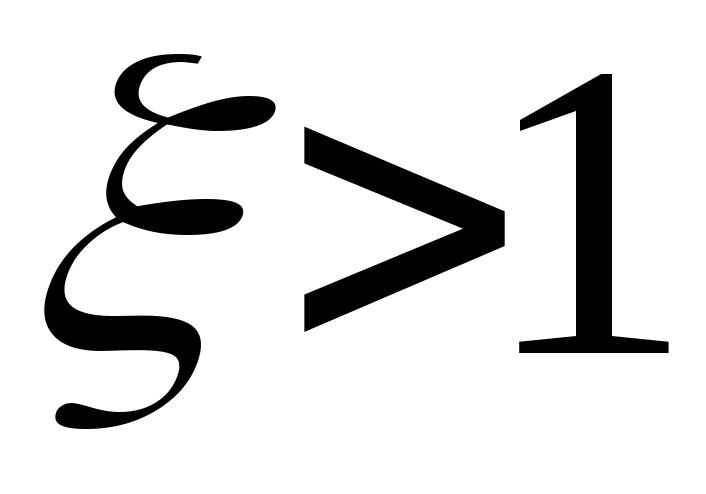 ,
то колебательное звено распадается на
два апериодических звена.
,
то колебательное звено распадается на
два апериодических звена.Если
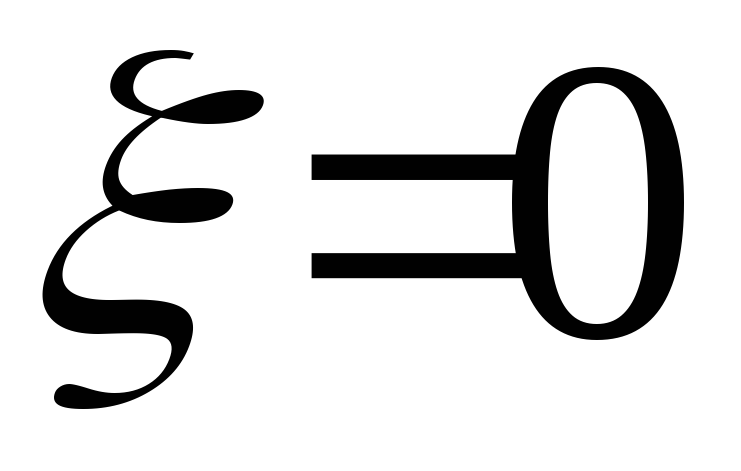 ,
то собственное движение колебательного
звена – незатухающие колебания с
частотой
,
то собственное движение колебательного
звена – незатухающие колебания с
частотой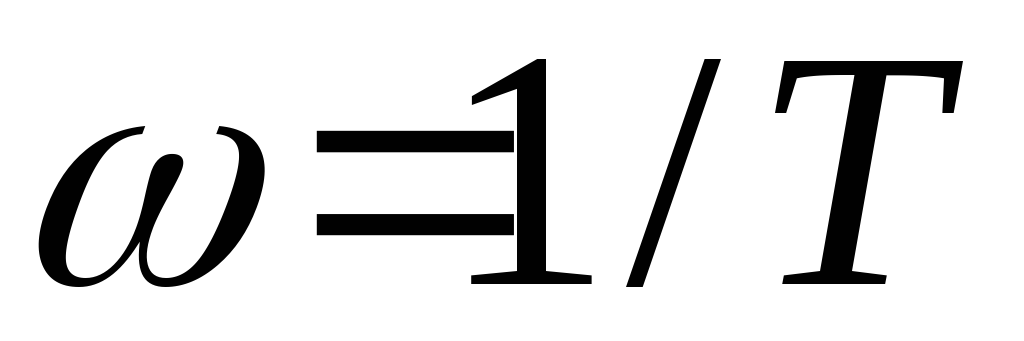 .
При
.
При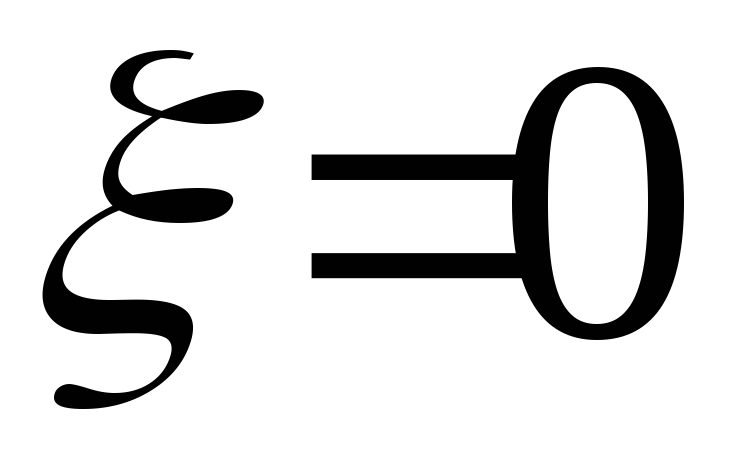 колебательное звено называется
консервативным.
колебательное звено называется
консервативным.
Характеристики колебательного звена.
Временные характеристики.
Переходная функция колебательного звена.
![]() ;
;
начальные условия для уравнения (2) – нулевые.
Общее решение однородного дифференциального уравнения (2) определяется равенством (5). Частное решение неоднородного уравнения
![]() (6)
(6)
будет
![]() .
Тогда решение неоднородного уравнения
(6) будет иметь вид
.
Тогда решение неоднородного уравнения
(6) будет иметь вид
![]() (7)
(7)
Постоянные интегрирования С1и С2 определяются нулевыми начальными условиями:
![]() ;
;![]() .
.
Имеем:
![]()
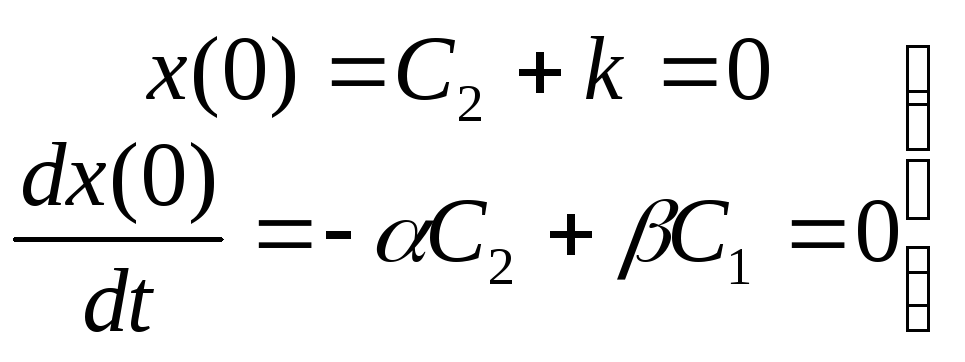
Это система линейных уравнений относительно постоянных интегрирования С1и С2.
Решение
этой системы уравнений с учётом значений
![]() и
и![]() даёт:
даёт:
![]() ;
;![]() .
.
Преобразуем равенство (7) следующим образом:
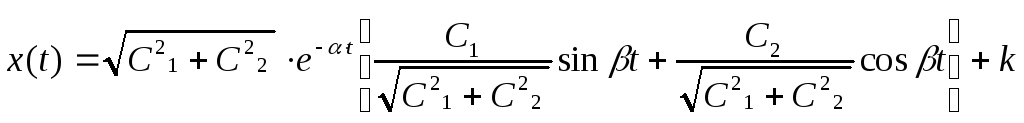 (8)
(8)
Обозначим
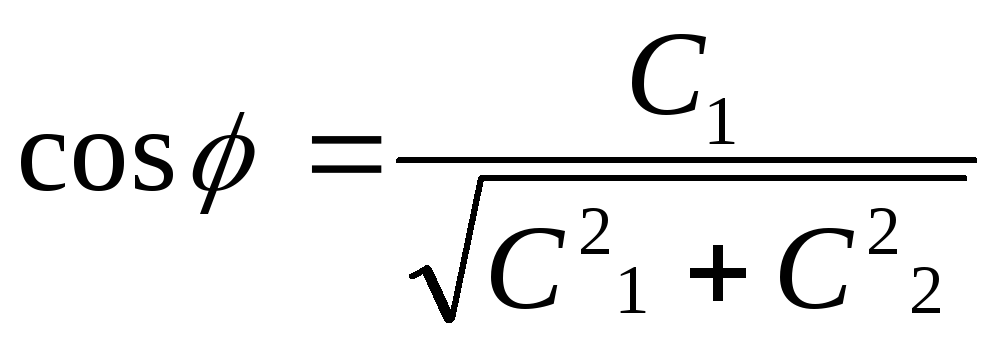 ;
;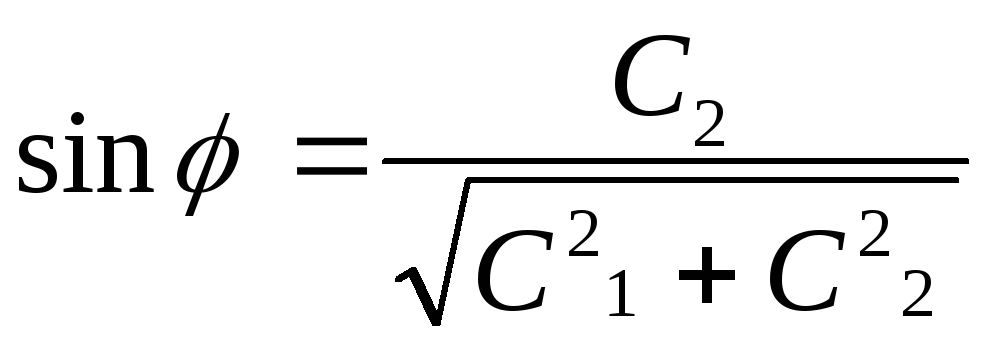 ;
;![]() .
.
Тогда равенство (8) принимает вид (с учётом вычисленных значений постоянных интегрирования С1и С2):
![]()
![]()
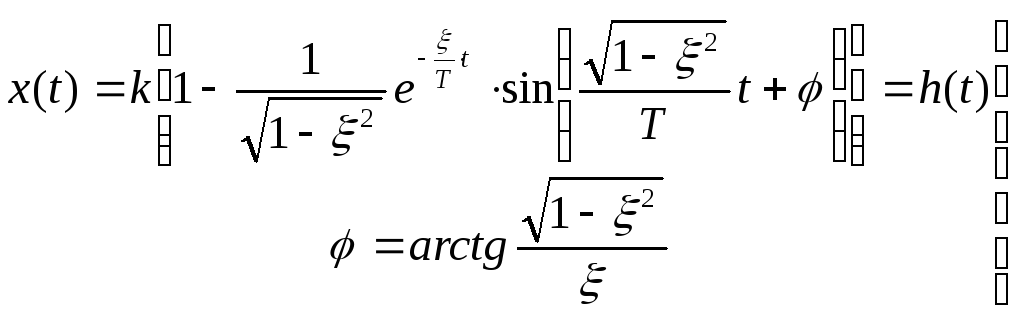 (9)
(9)
Полученное
уравнение (9) описывает затухающий
колебательный процесс (откуда и название
звена – колебательное) с относительным
коэффициентом затухания
![]() и частотой
и частотой![]() .
Установившееся значение переходной
функции определяется как
.
Установившееся значение переходной
функции определяется как
![]()
график функции
![]() имеет вид, показанный на рисунке.
имеет вид, показанный на рисунке.
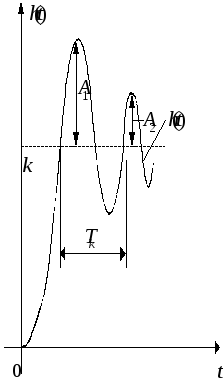
![]() -
период колебаний;
-
период колебаний;
![]() -
амплитуды двух соседних колебаний
относительно установившихся значений.
-
амплитуды двух соседних колебаний
относительно установившихся значений.
По графику функции
![]() можно определить параметры колебательного
звена следующим образом:
можно определить параметры колебательного
звена следующим образом:
Коэффициент усиления колебательного звена определяют по установившемуся значению переходной функции
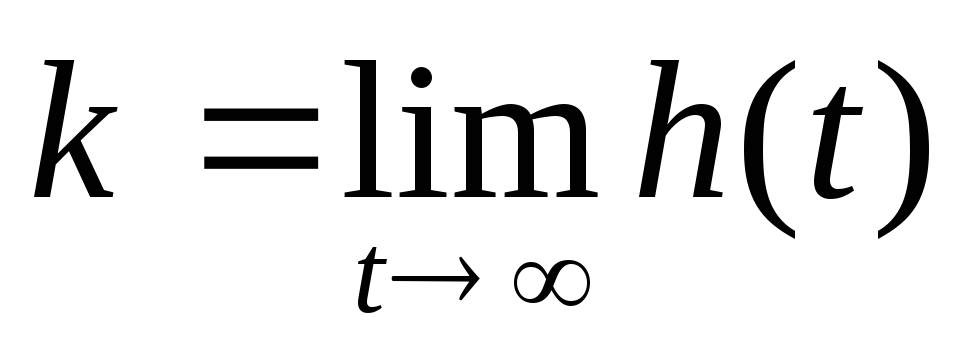 .
.Постоянную времени Т и коэффициент затухания
 можно найти из уравнений
можно найти из уравнений
![]() ;
;![]() .
.
Весовая функция колебательного звена.
Так
как весовая функция
![]() равна производной по времени переходной
функции, то из равенства (9) следует
равна производной по времени переходной
функции, то из равенства (9) следует
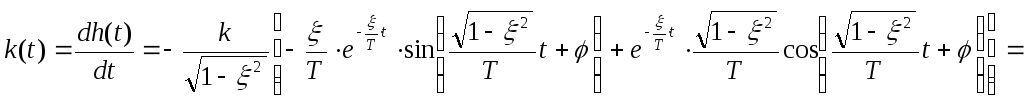
![]() (10)
(10)

