Характеристики систем автоматического управления и их звеньев.
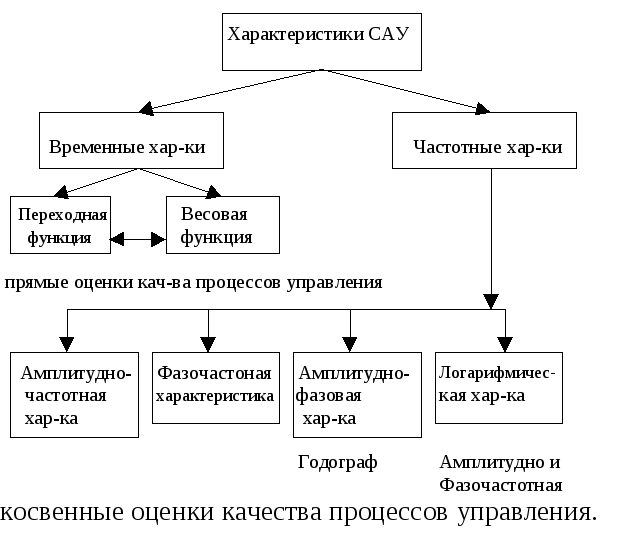
Различают два основных типа характеристик систем автоматического управления и их звеньев:
1. Временные характеристики;
2. Частотные характеристики.
Временные характеристики систем автоматического управления и их звеньев.
Временными характеристиками систем автоматического управления и их звеньев являются:
1. Переходная функция систем автоматического управления или ее звена.
Обозначение:
2. Весовая функция системы автоматического управления или ее звена.
Обозначение:
Весовую функцию системы (звена) иногда называют импульсной переходной функцией.
Временные характеристики системы управления и ее элементов можно получить:
1. Решая дифференциальное уравнение, являющееся математической моделью системы или ее элемента.
2. Используя аппарат передаточных функций.
- характеристики элементарных звеньев;
- характеристики разомкнутых систем;
- характеристики замкнутых систем.
Временные характеристики систем управления и их звеньев.
Временные характеристики систем автоматического управления и их звеньев являются:
1. Переходная функция системы управления или ее звена:
2. Весовая или переходная импульсная функция системы или ее звена:
Временные характеристики можно получить:
1. Решая дифференциальные уравнение, являющиеся математической моделью системы или ее элемента.
2. Используя аппарат передаточных функций.
ПЕРЕХОДНАЯ ФУНКЦИЯ.
Переходной функцией систем автоматического управления (ее звена) называют функцию описывающую изменение выходной величины, когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях.
Если в качестве математической модели системы используется передаточная функция, то можно получить:
,
,
.
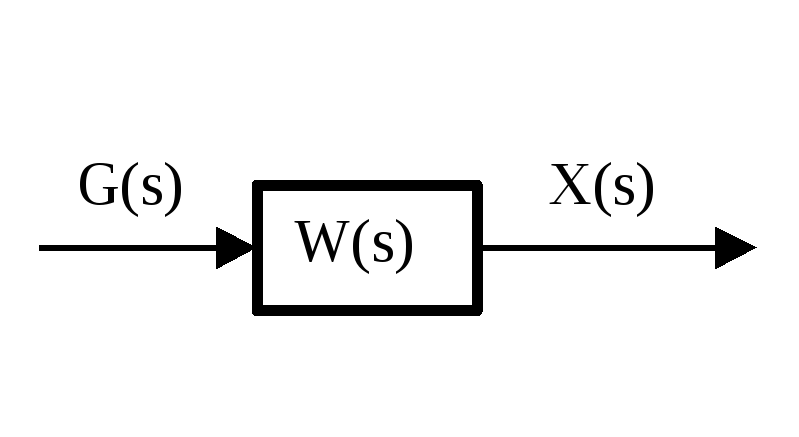
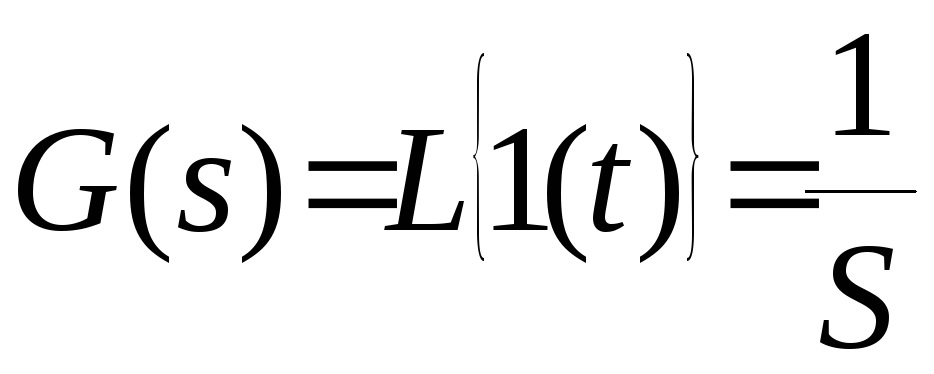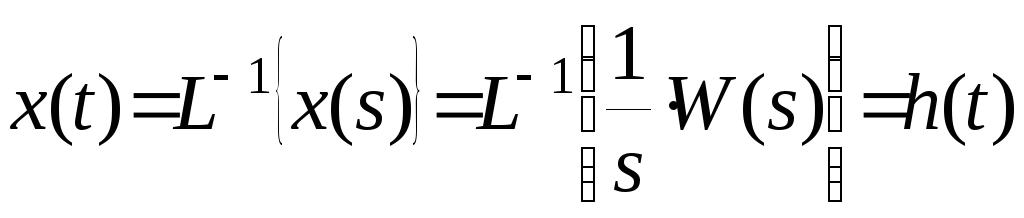Следовательно,
переходная функция
определяется по правилу:
.
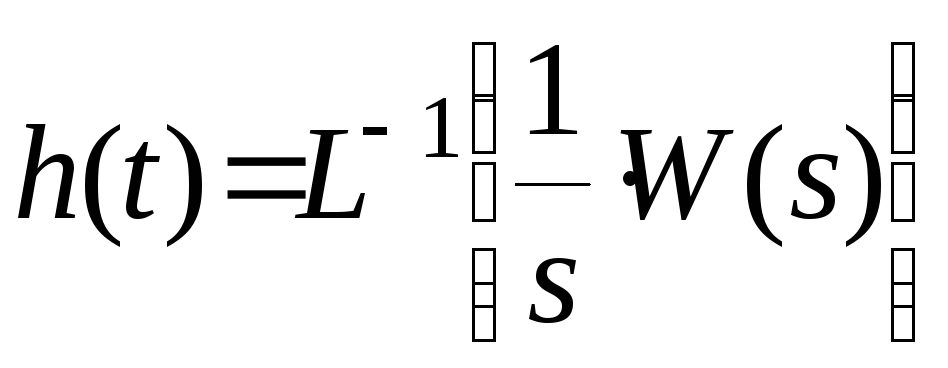ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ (ВЕСОВАЯ) ФУНКЦИЯ.
Весовая
функция (импульсная переходная функция)
называется функция, которая описывает
реакцию системы, когда на ее вход подается
-функция
при нулевых начальных условиях.
Если в качестве математической модели системы управления принята передаточная функция, то можно получить:
,
,
.
Следовательно,
весовая функция
системы управления определяется
равенством:
.
СВЯЗЬ МЕЖДУ ПЕРЕХОДНОЙ И ВЕСОВОЙ ФУНКЦИЯМИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
Из определений переходной и весовой функций автоматического управления имеем:
;
;
.
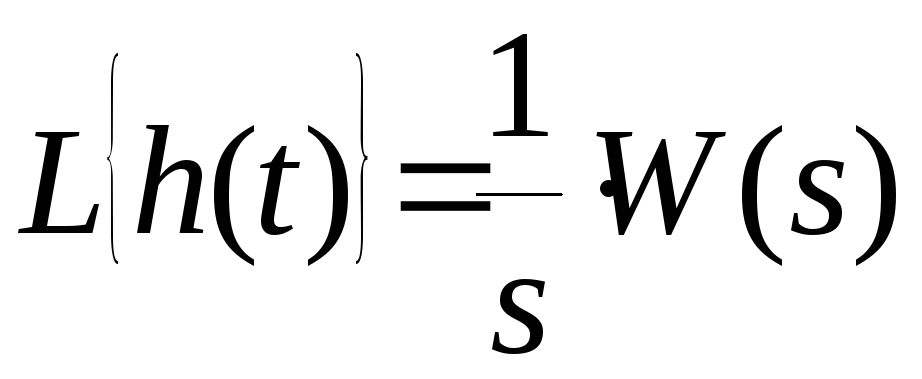Сравнивая
эти два равенства нетрудно заметить,
что
.
Из свойства преобразования Лапласа
видно, что при нулевых начальных условиях
умножение изображения на
соответствует дифференцированию по
в области оригиналов, т.е.
.
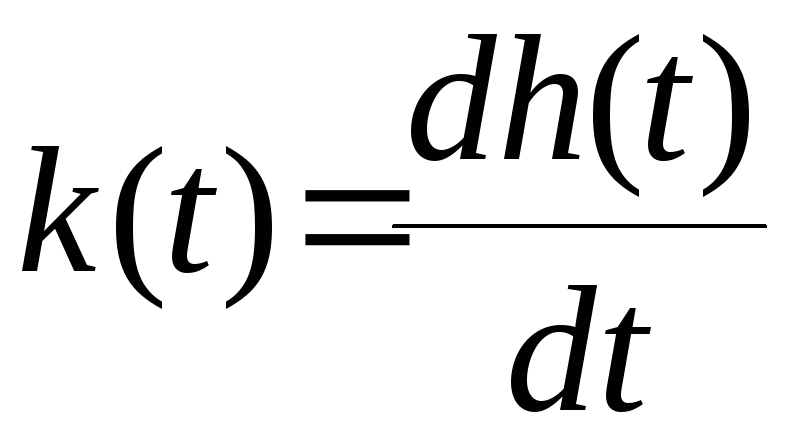Весовая
и переходная функции являются
исчерпывающими характеристиками систем
автоматического управления при нулевых
начальных условиях. По этим характеристикам
можно однозначно определить выходную
переменную
системы при произвольном входном
воздействии
по формуле:
.
ПЕРЕХОДНАЯ ФУНКЦИЯ.
Переходной функцией системы автоматического управления, ее звена, называют функцию, описывающую изменение выходной величины системы (ее звена), когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях.
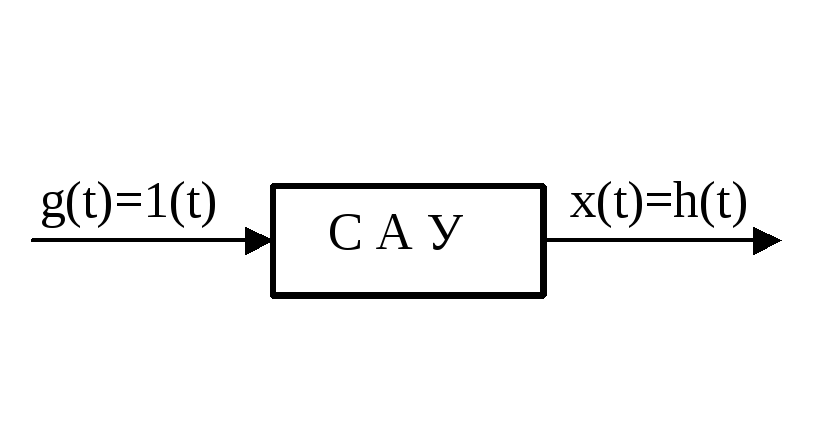
Если в качестве математической модели системы автоматического управления используется передаточная функция, то имеем:
,
,
.
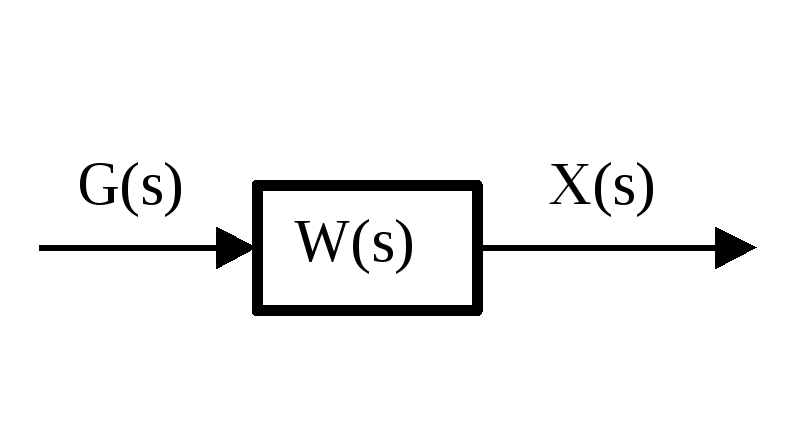
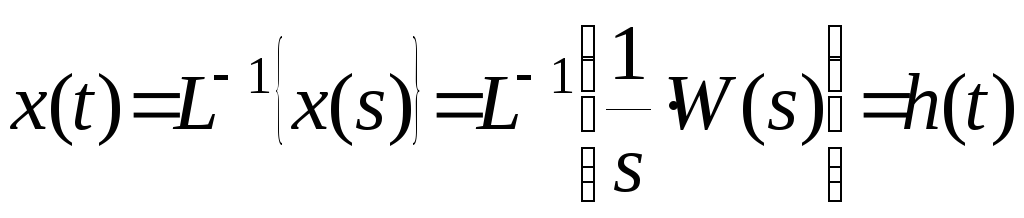Следовательно,
переходная функция
определяется по правилу:
.
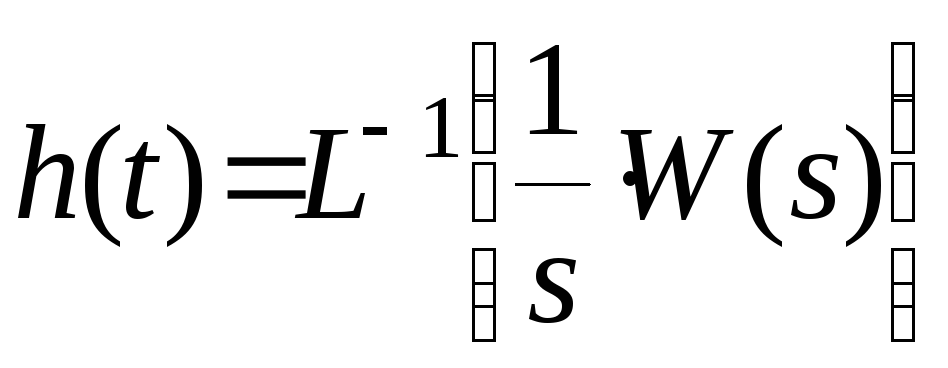Таким образом, для определения переходной функции системы автоматического управления или ее звена надо:
Получить передаточную функцию системы автоматического управления или ее звена:
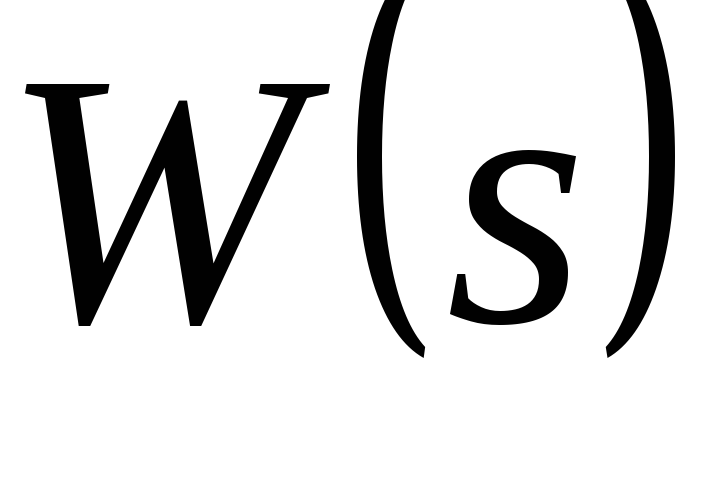.Найти обратное преобразование Лапласа от выражения
.
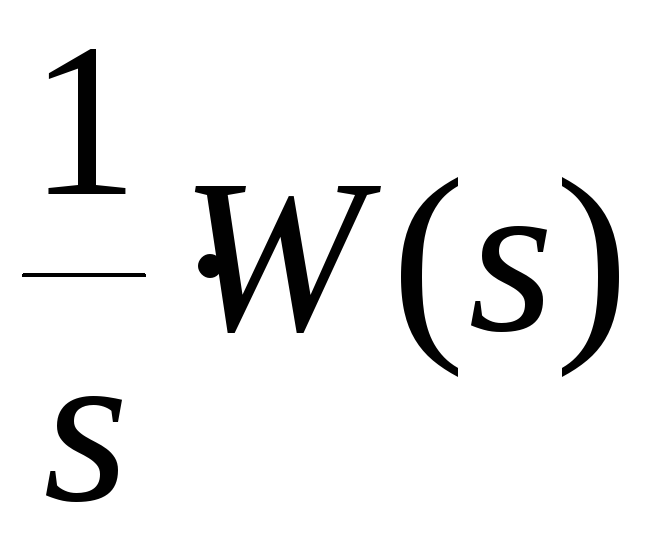Это и будет переходной функцией системы
автоматического управления или ее
элемента:
.
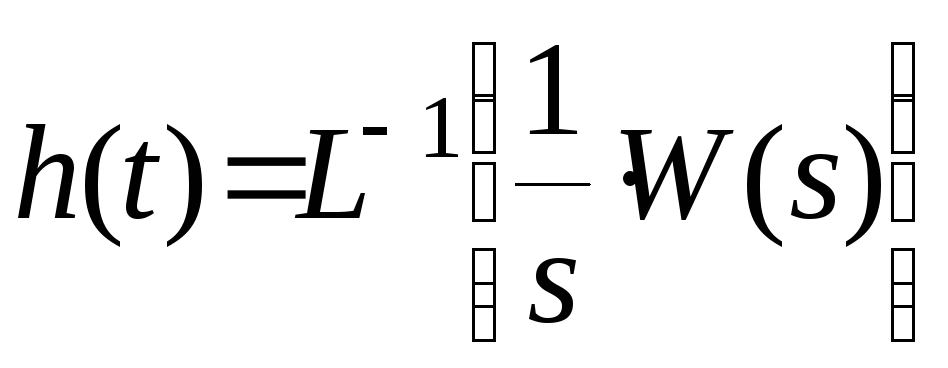ИМПУЛЬСНАЯ ПЕРЕХОДНАЯ (ВЕСОВАЯ) ФУНКЦИЯ.
Весовая
функция системы автоматического
управления (ее звена) называют функцию,
описывающую реакцию системы (звена),
когда на ее вход подается
-функция
при нулевых начальных условиях.
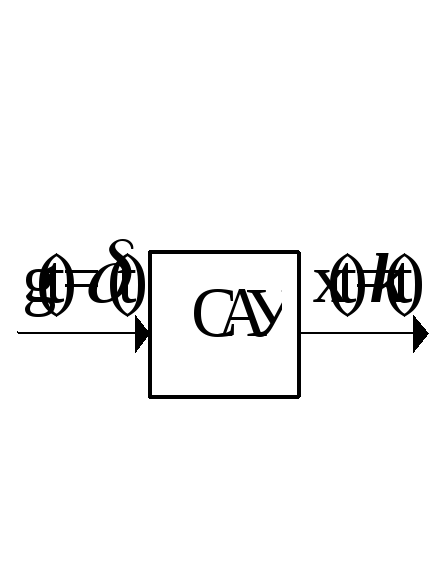
Если в качестве математической модели системы управления принята передаточная функция, то можно получить:
,
;
.
Следовательно,
весовая функция
системы управления определяется
равенством:
.
Таким образом, для определения весовой функции системы автоматического управления или ее звена надо:
Получить передаточную функцию системы автоматического управления или ее звена:
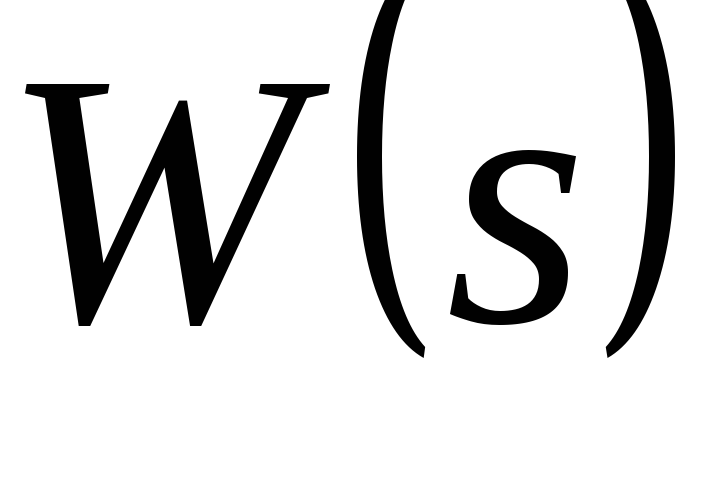.Найти обратное преобразование Лапласа от выражения
системы или ее звена. Это и будет весовой
функцией системы автоматического
управления или ее звена:
.
СВЯЗЬ МЕЖДУ ПЕРЕХОДНОЙ И ВЕСОВОЙ ФУНКЦИЯМИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
Из определений переходной и весовой функций автоматического управления имеем:
,
.
Последнее равенство означает, что передаточная функция системы автоматического управления определяется как преобразование Лапласа от весовой функции.
Сравнивая эти два равенства нетрудно заметить, что
.
Из свойств преобразований Лапласа видно, что при нулевых начальных условиях умножение изображения на S соответствует дифференцированию по t в области оригиналов, т.е.
.
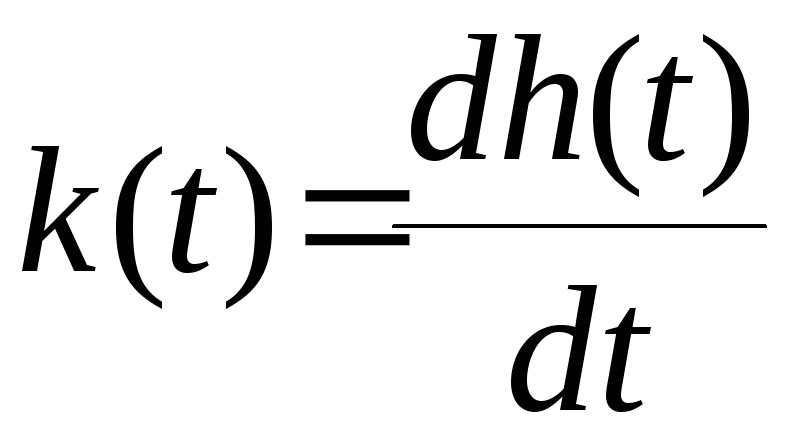Весовая
и переходная функции, как и передаточная
функция являются исчерпывающими
характеристиками систем автоматического
управления при нулевых начальных
условиях. По этим характеристикам можно
однозначно определить выходную переменную
системы при произвольном входном
воздействии
по формуле:
.
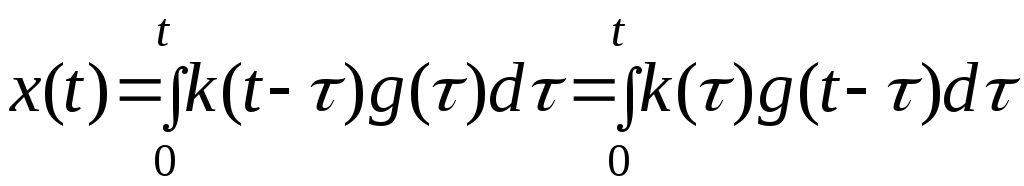В качестве примера рассмотрим звено системы автоматического управления, которое представляет собой RC-контур.
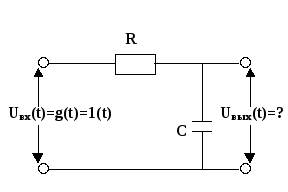
Ранее были получены математические модели данного RC-контура в виде дифференциального уравнения первого порядка:
(1)
и в виде передаточной функции:
.
(2)
Определим
,
решая дифференциальное уравнение (1)
при нулевых начальных условиях и
используя формулу связи переходной
функции с передаточной функцией системы:
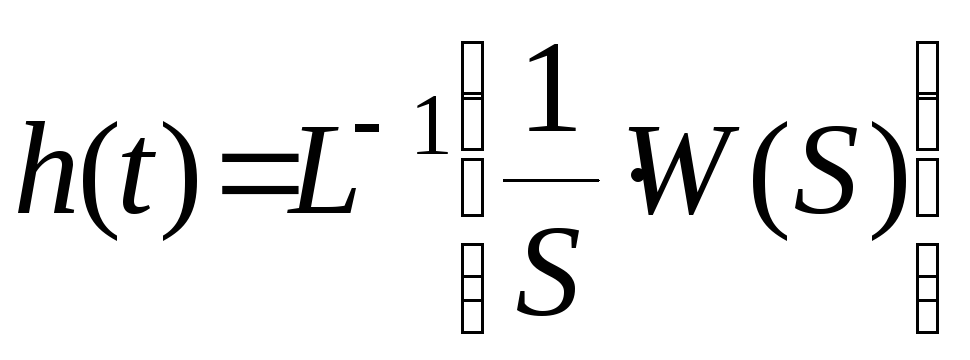(3)
Ранее
было получено решение уравнения (1) при
нулевых начальных условиях и
в следующем виде:
.
В
нашем случае последнее равенство
принимает вид
:
.
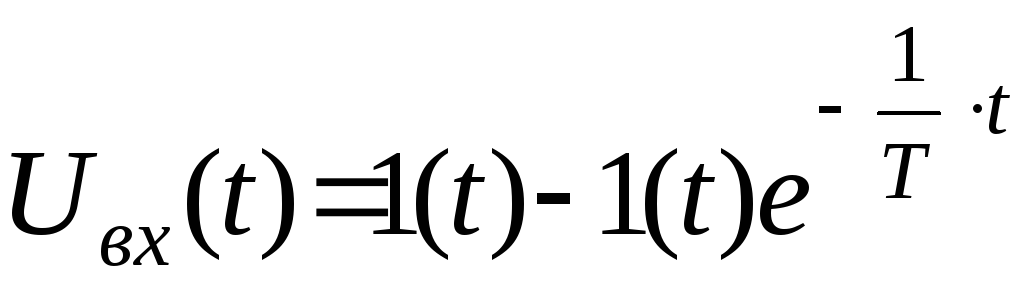По
определению переходной функции
.
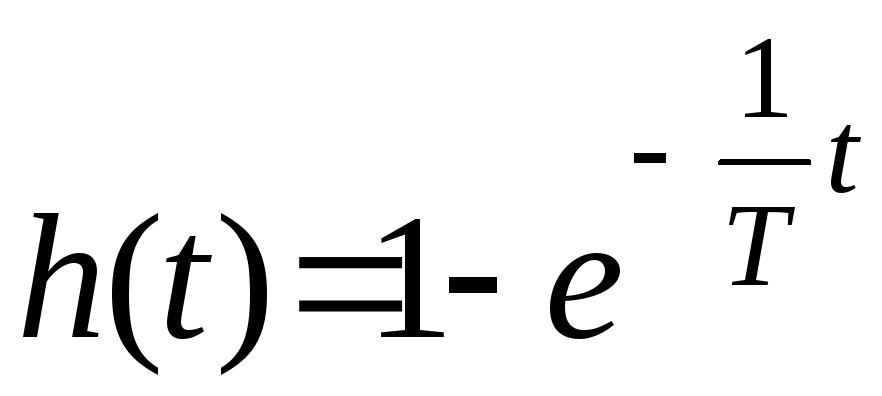
(4)
Получим
с помощью равенства (3):
.
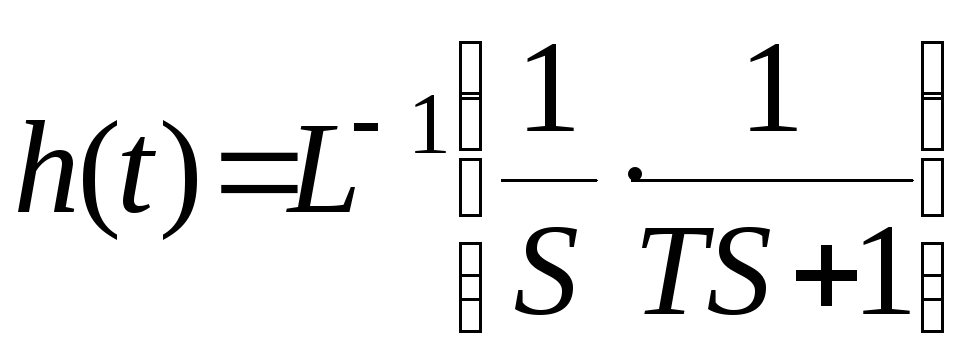Выполним
обратное преобразование Лапласа
используя разложение дробно-рациональной
функции
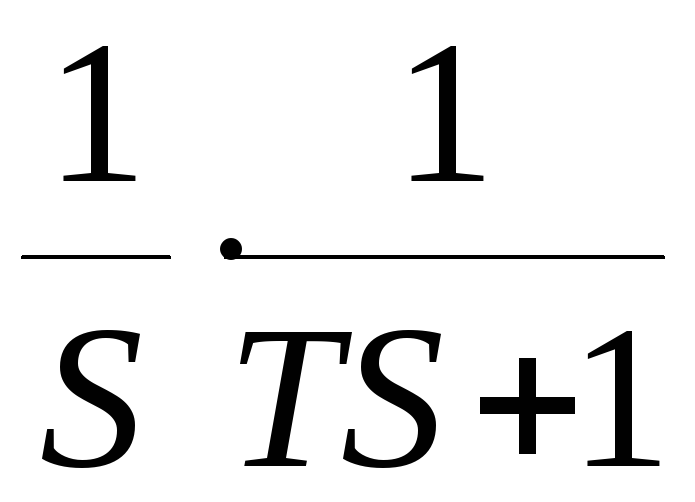на сумму элементарных дробей. Имеем:
-
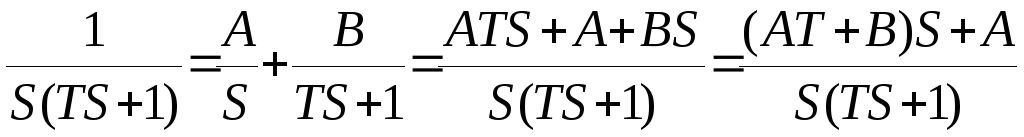
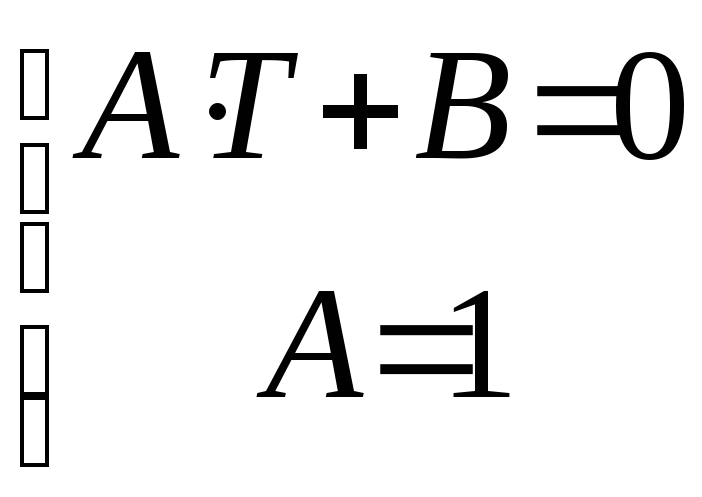система линейных алгебраических
уравнений относительно
и
.
Решение системы уравнений:
,
.
Таким образом:
.
Следовательно:
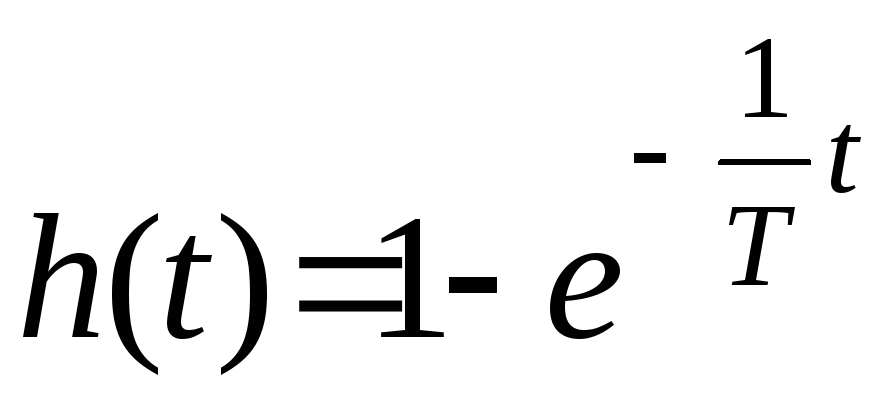(5)
Выражения (4) и (5) совпадают.
Весовая функция (импульсная переходная функция):
(6)
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
Частотные характеристики систем управления и их звеньев получаются рассмотрением вынужденных движений системы (звена) при подаче на ее вход гармонического сигнала
,
(1)
где
– амплитуда входного сигнала;
- его частота.
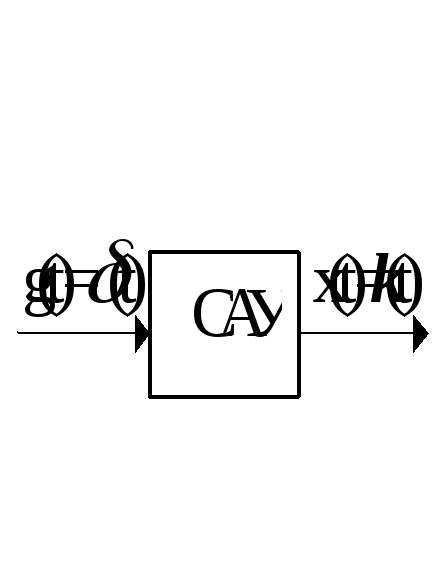
Возникает естественный вопрос какой вид сигнала будет на выходе системы, если на его вход подать гармонический сигнал (1).
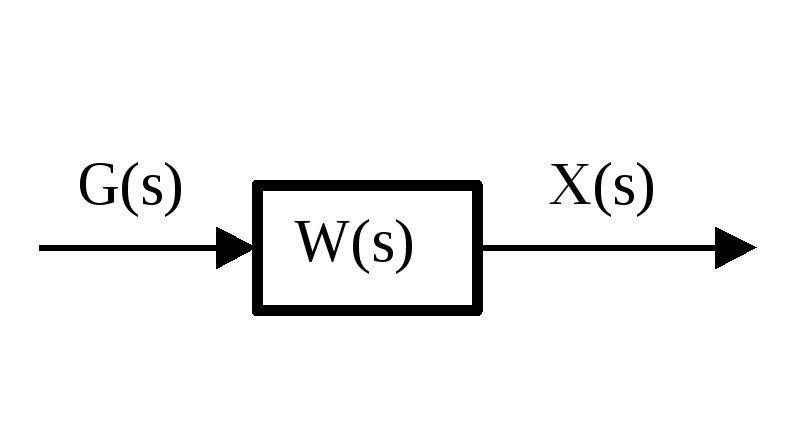
Ранее был получен следующий результат. Если на вход звена системы управления с передаточной функцией
,
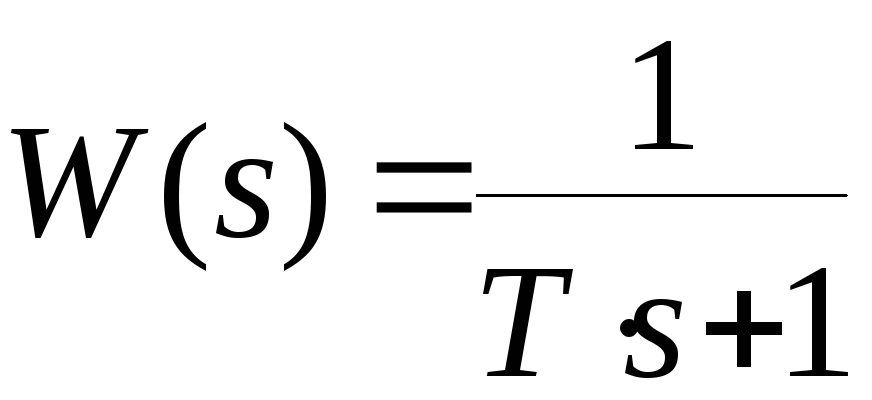(2)
поступает гармонический сигнал (1), то на выходе этого звена в установившемся режиме будет также гармонический сигнал
,
(3)
такой
же частоты, что и входной сигнал 
,
но амплитуда 
и
сдвиг по фазе 
зависят от частоты входного сигнала 
:
;
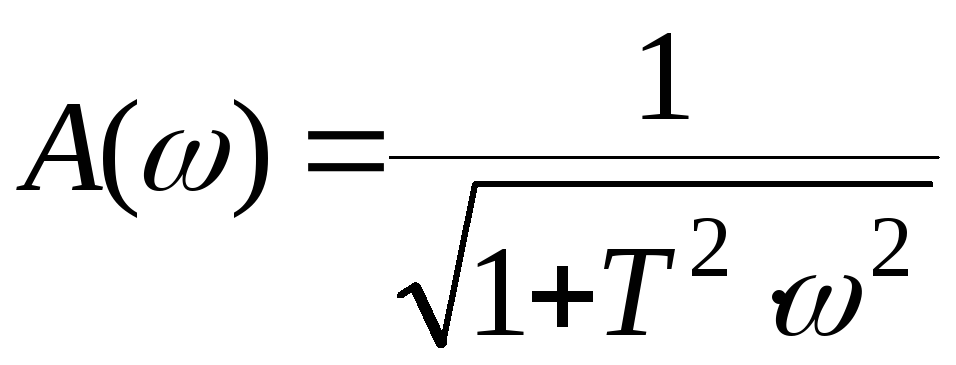, (4)
(для функции (2)).
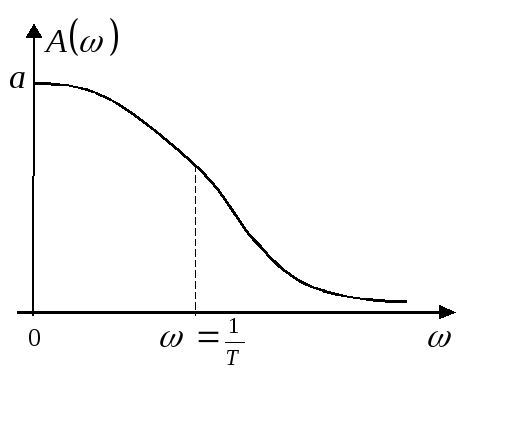
Величина
называется амплитудно - частотной
характеристикой системы управления и
определяет изменение амплитуды
гармонического входного сигнала при
прохождении его через заданную систему
в зависимости от частоты входного
воздействия.
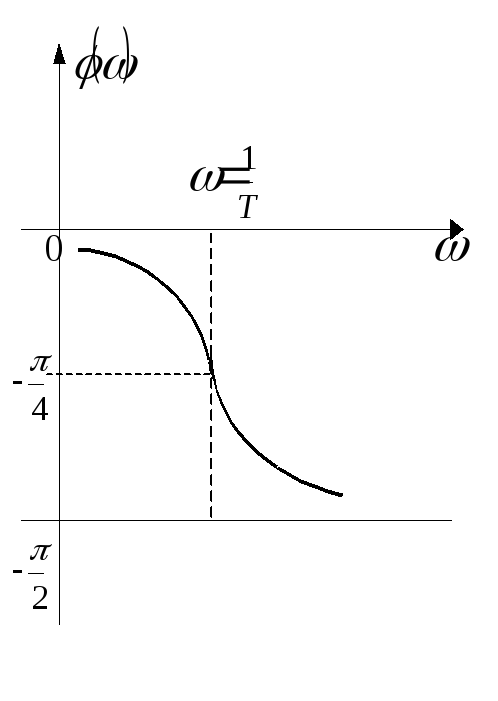
Величина
называется фазо - частотной характеристикой
системы управления и устанавливает
изменение фазы выходного сигнала системы
в зависимости от частоты входного
гармонического сигнала.
Способы аналитического определения частотных характеристик.
Различают два основных способа определения частотных характеристик систем автоматического управления:
Частное решение неоднородного дифференциального уравнения.
По передаточным функциям системы управления.
Каждый из этих способов рассмотрим на простейшем примере, когда система управления описывается дифференциальным уравнением первого порядка
,
(1)
либо имеет передаточную функцию вида
,
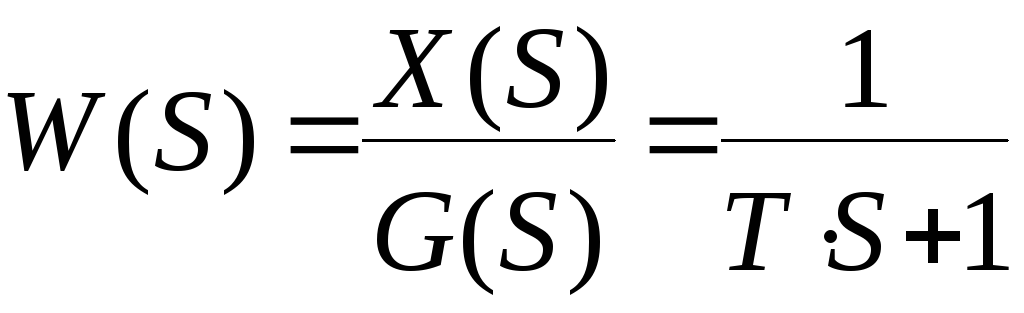(2)
В первом случае частотные характеристики определяются как частное решение неоднородного дифференциального уравнения (1) – вынужденное движение системы.
Так
как правая часть уравнения (1) имеет вид
,
то частное решение неоднородного
уравнения будем искать в виде
,
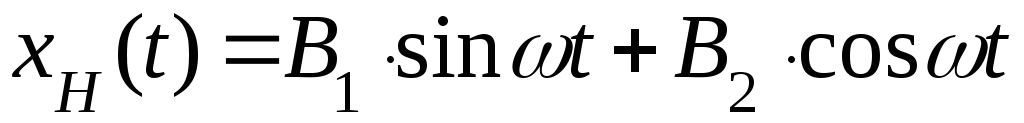(3)
где
коэффициенты
и
подлежат определению. Для этой цели
подставим (3) в уравнение (1), в результате
чего получаем
.
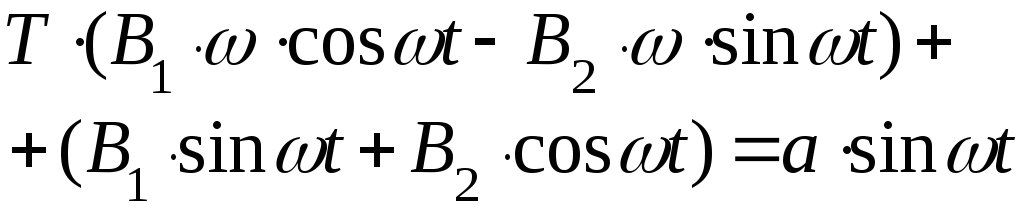Преобразуем последнее равенство
.
Для
определения значений
и
приравняем в последнем равенстве
коэффициенты при
и 
:
,
.
(4)
Это
система линейных уравнений относительно
неизвестных
и
.
Решим её:
;
.
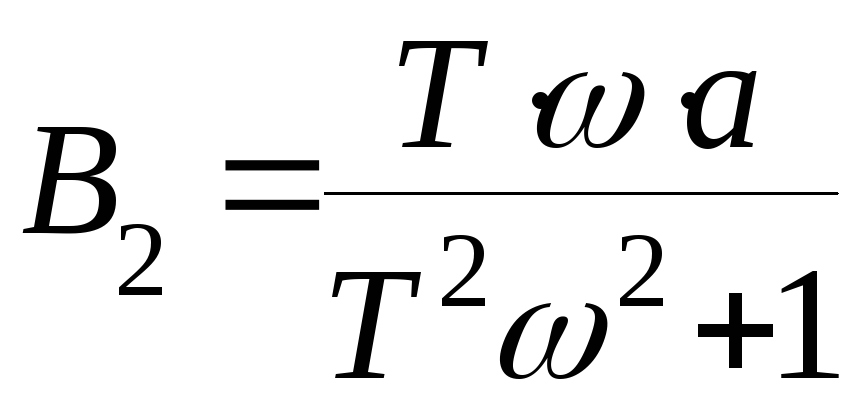Подставим полученные равенства в уравнение (3), получим
.
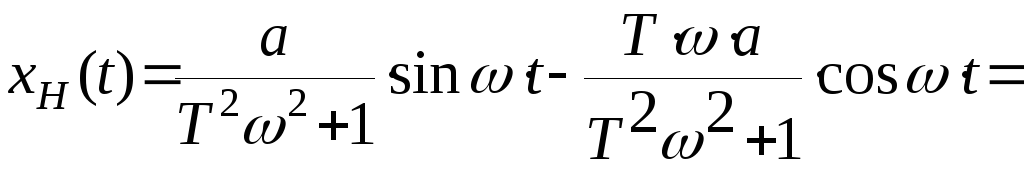
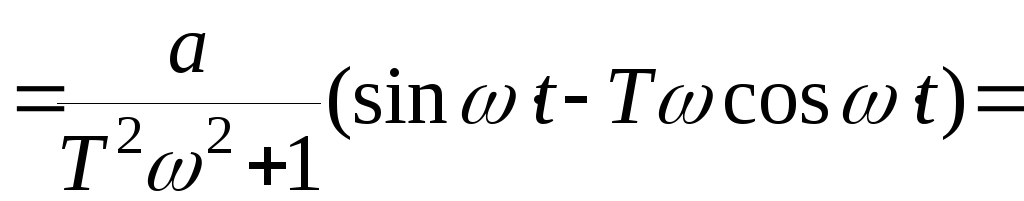
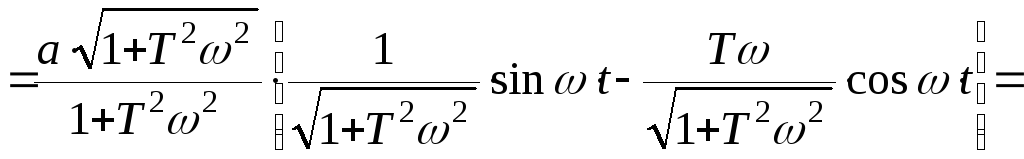
Здесь:
;
; 
.
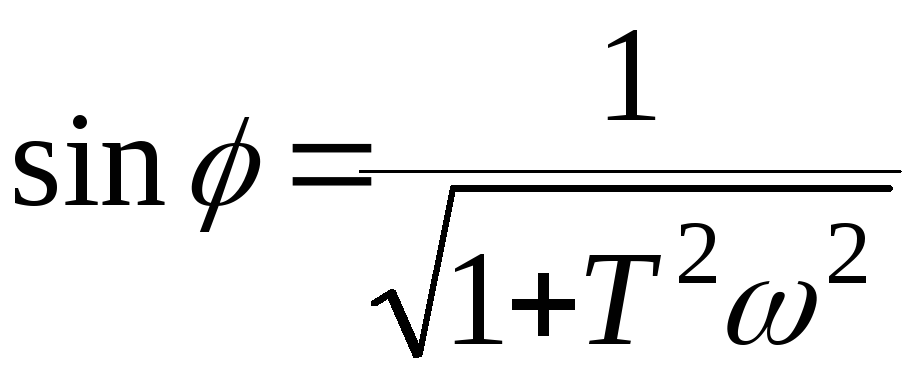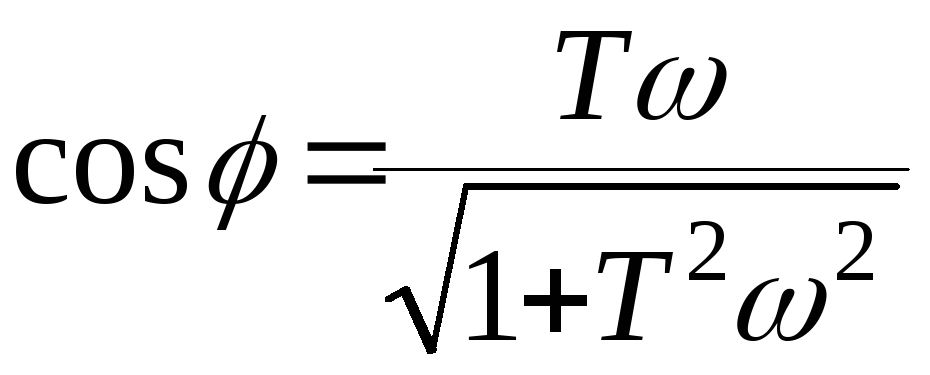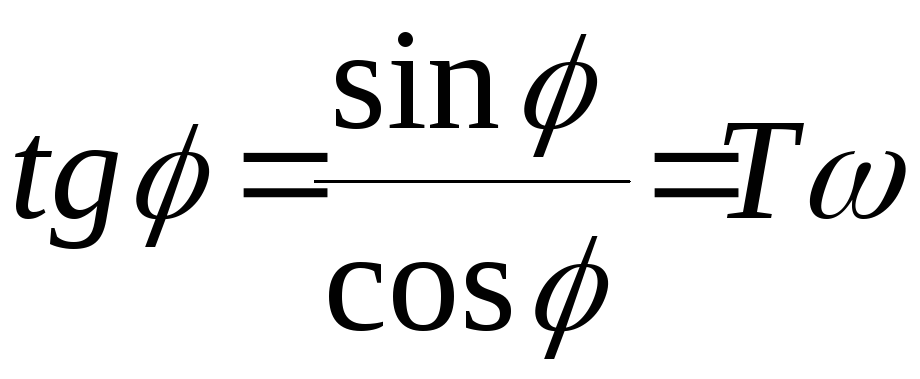Итак, окончательно имеем:
,
.
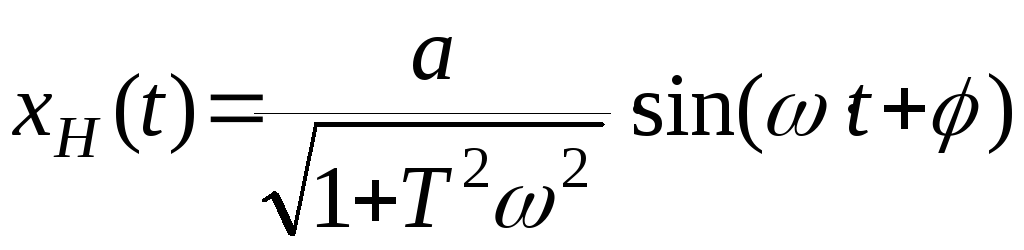(5).
Равенства (5) позволяют сделать следующие выводы.
Если на вход системы управления поступает гармонический входной сигнал
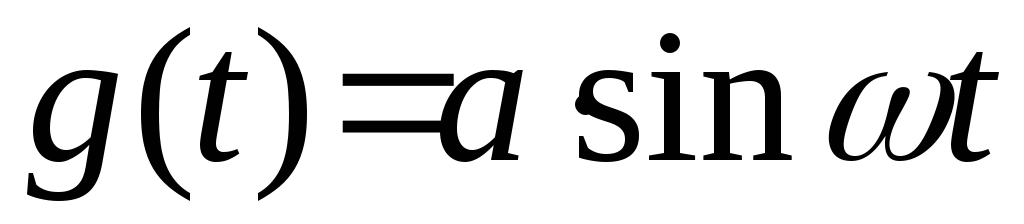амплитуды 
и частоты 
,
то выходной сигнал системы также будет
гармоническим сигналом частотой 
.
Амплитуда выходного сигнала определяется равенством
,
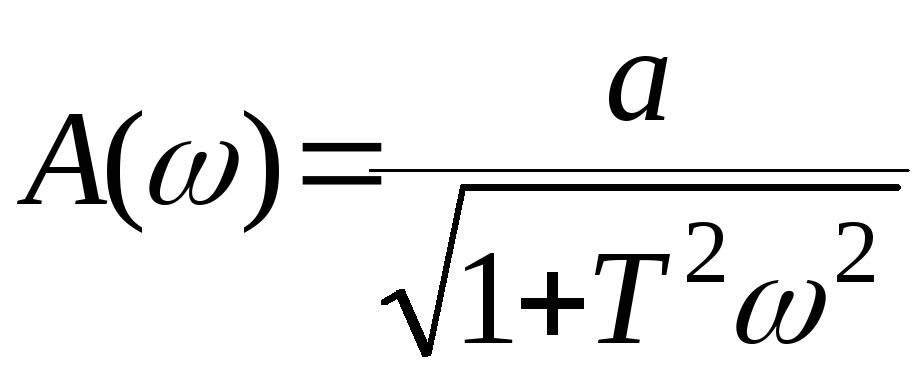(6)
а его фаза равна
.
(7).
Это значит, что
амплитуда и фаза выходного сигнала
системы управления являются функциями
частоты входного сигнала
.
Теперь установим связь частотных характеристик системы автоматического управления с ее передаточной функцией.
Пусть передаточная функция системы имеет вид
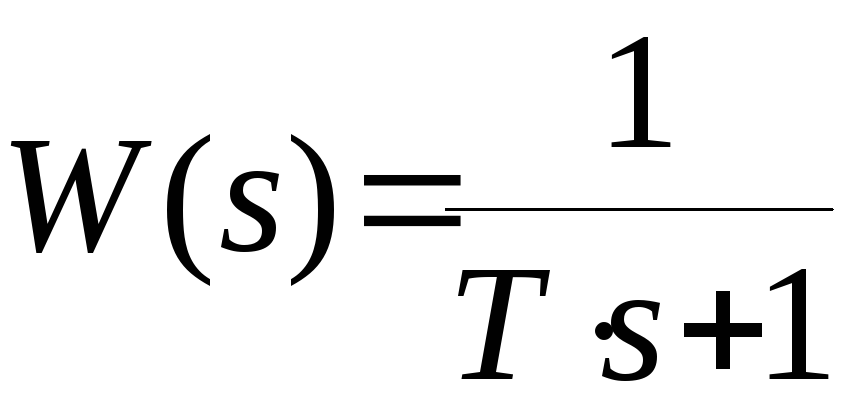. (8)
Выполним в равенстве
(8) замену переменной
,
в результате чего последовательно
получаем
.
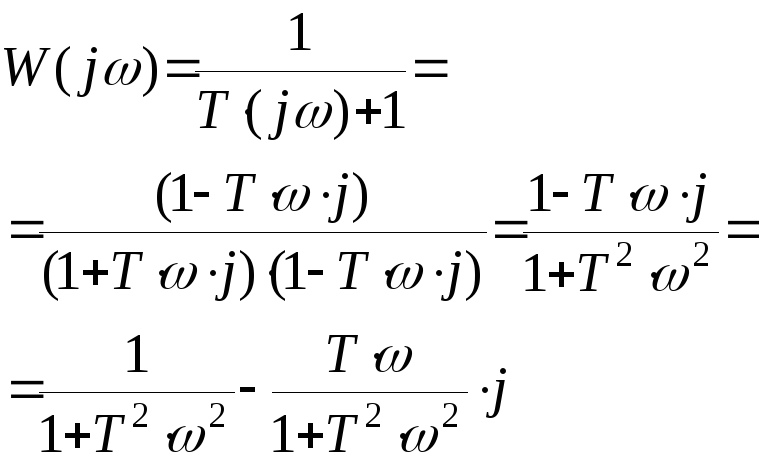Вычислим модуль и
аргумент комплексного числа
:
,
. (9)
,
.
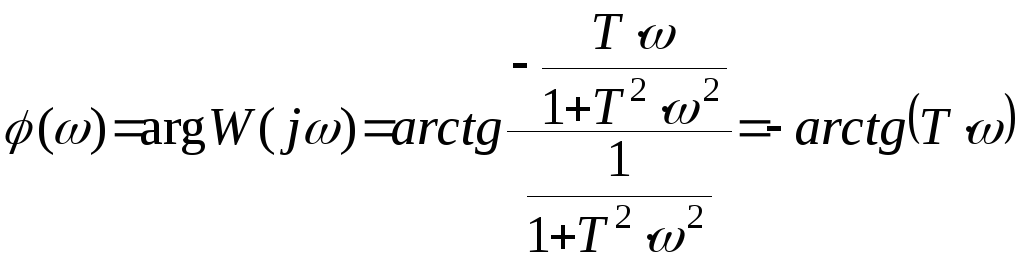(10)
Равенство
(10) в точности совпадает с равенством
(7), а равенство (9) совпадает с равенством
(6) с точностью до множителя
– амплитуды входного гармонического
сигнала. Так как
в равенстве (6) выбирается исследователемпроизвольно, то в (6) можно полагать
.
Обобщим сказанное.Пусть передаточная функция системы управления имеет вид
.
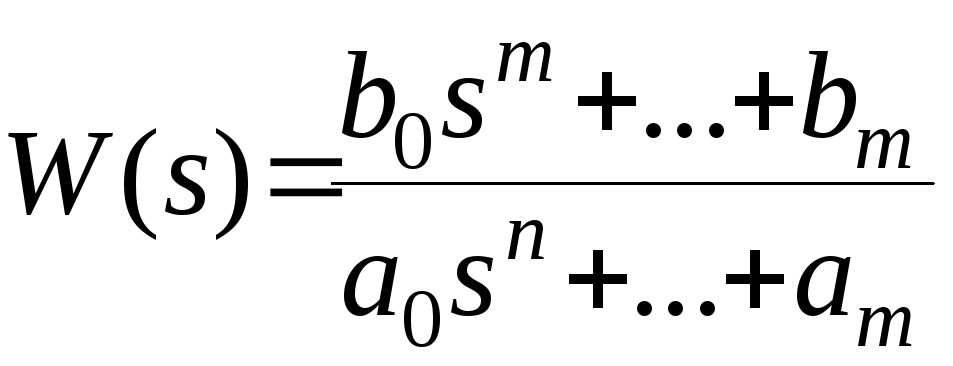(11)
В последнее равенство
подставим
и комплексное число
представим в виде
, (12)
где
- действительная часть комплексного
числа
;
- мнимая часть комплексного числа
.
Модуль комплексного
числа
- это амплитудно частотная характеристика
системы, т.е.
. (13)
Аргумент комплексного
числа
- это фазочастотная характеристика
системы управления, т.е.
. (14)
На комплексной
плоскости W (см. рисунок) комплексное
число
изображается
вектором ОС, длина которого равна
,
а аргумент
- это угол образованный этим вектором
с действительной положительной полуосью
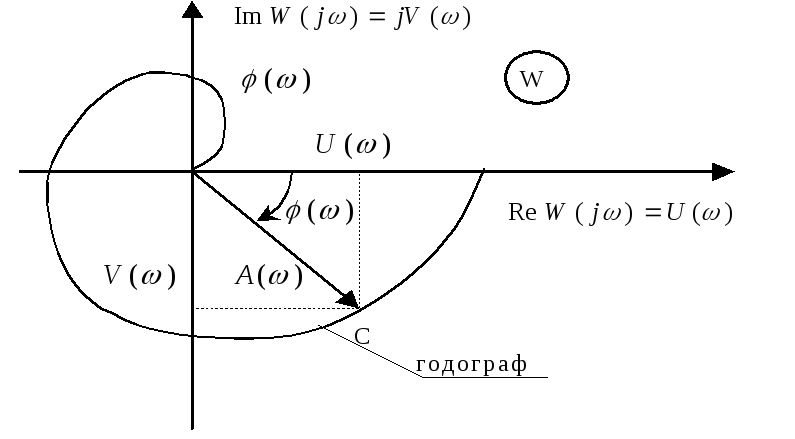
При изменении частоты
от 0 до
конец вектора ОС (точка) опишет некоторую
кривую, которая называется годографом
амплитудно-фазо-частотной характеристики.
Годограф
амплитудно-фазо-частотной характеристики
– это кривая, которая получается, если
в передаточной функции системы
автоматического управления положить
и изменяя
от
до
на плоскости
наносить вычисленные значения
и
.
В практике исследований систем автоматического управления широко применяются логарифмические амплитудно-частотные и фазо-частотные характеристики.
Логарифмическая
амплитудно-частотная характеристика
системы автоматического управления –
это кривая, соответствующая двадцати
десятичным логарифмам модуля
,
построенной в десятичном логарифмическом
масштабе частот – размерность децибел.
.
Логарифмическая
фазо-частотная характеристика системы
автоматического управления – это её
фазо-частотная характеристика
,
построенная в логарифмическом масштабе
частот.
Ценность частотных характеристик состоит в том, что они позволяют косвенно судить о процессах, происходящих в системах автоматического управления (не решая дифференциальных уравнений, описывающих данную систему).
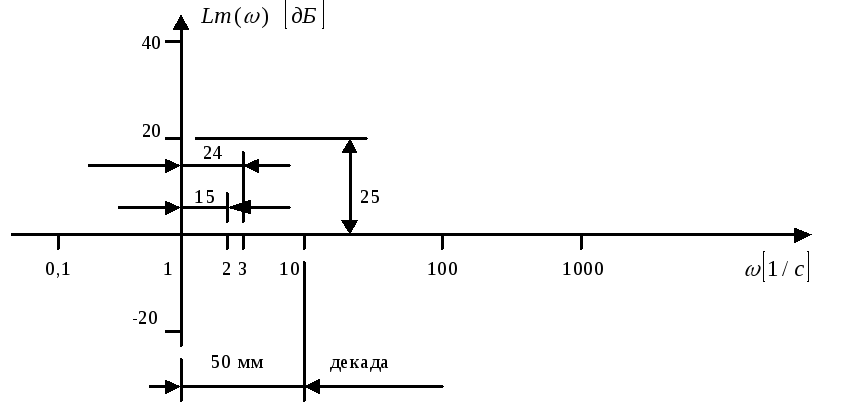
Для построения
логарифмической амплитудно-частотной
характеристики принято брать более
мелкую единицу измерения, которая в 20
раз меньше одной десятичной логарифмической
единицы, т.е.
.
.
Данная единица
измерения называется децибел
.
ЭЛЕМЕНТАРНЫЕ ЗВЕНЬЯ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
И ИХ ХАРАКТЕРИСТИКИ.
Раньше звено системы автоматического управления было определено как математическая модель элемента, соединение элементов или любой части системы.
Вообще же звеном называют математическую модель элемента, соединения элементов или любой части системы.
Звенья, как и системы, могут описываться дифференциальным уравнением довольно высокого порядка и в общем случае их передаточные функции можно представить в виде
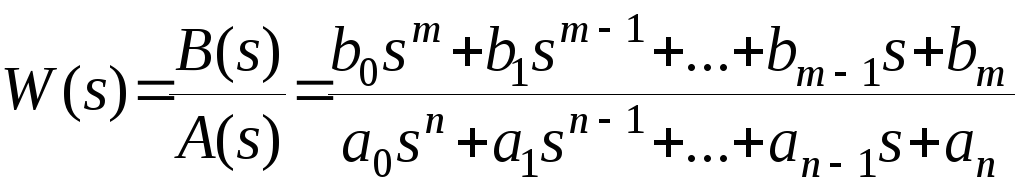. (1)
Но всегда их можно представить как соединения типовыхилиэлементарныхзвеньев, порядок дифференциальных уравнений которых не выше второго.
Из курса математики известно, что полином произвольной степени можно разложить на простые множители – множители вида:
,
,
. (2)
Поэтому передаточную функцию (1) можно представить как произведение простых множителей вида (2) и простых дробей вида:
,
,
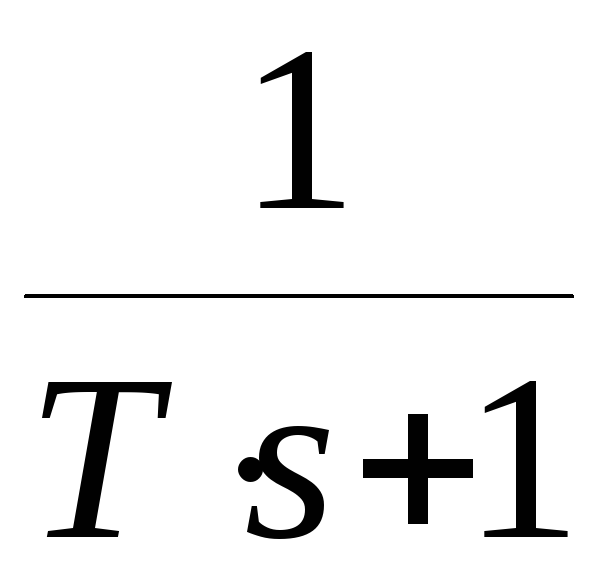. (3).
Звенья, передаточные функции которых имеют вид простых множителей (2) или простых дробей (3) называют типовымиилиэлементарнымизвеньями.
ПРИМЕР .
;
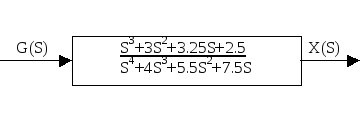
Корни числителя передаточной функции
Корни полинома знаменателя передаточной функции
Поэтому:
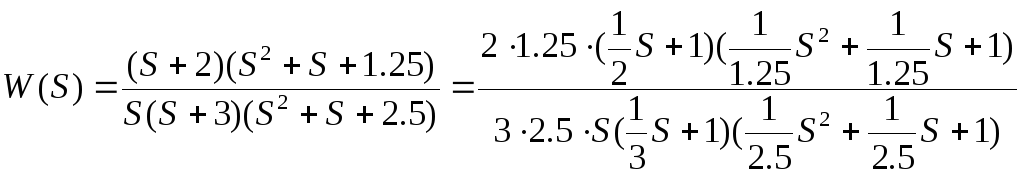
Введём обозначения:
(S2):
(S):
(S2):
(S):
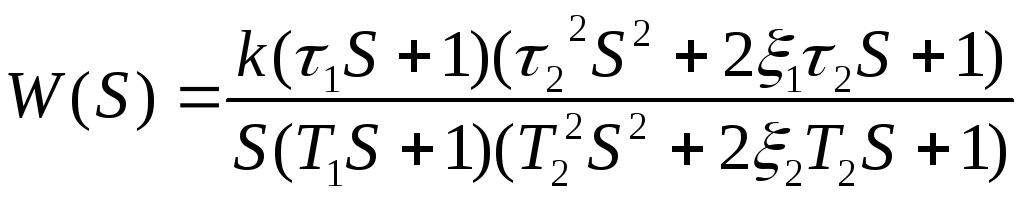
УСИЛИТЕЛЬНОЕ ЗВЕНО .
Математические модели:
;
.
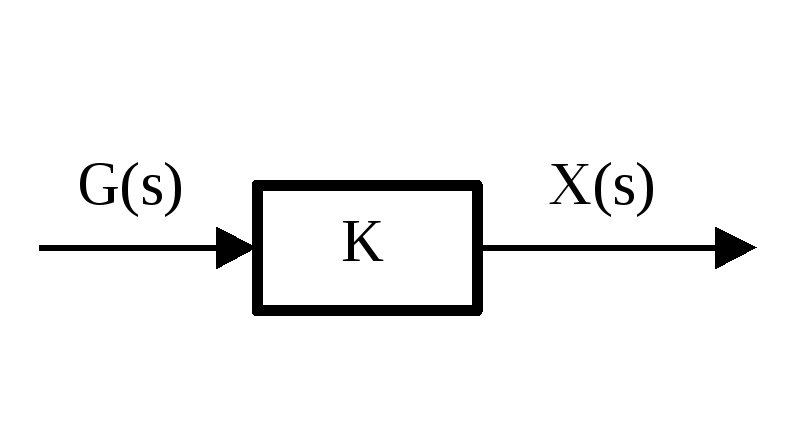
Временные характеристики:
.
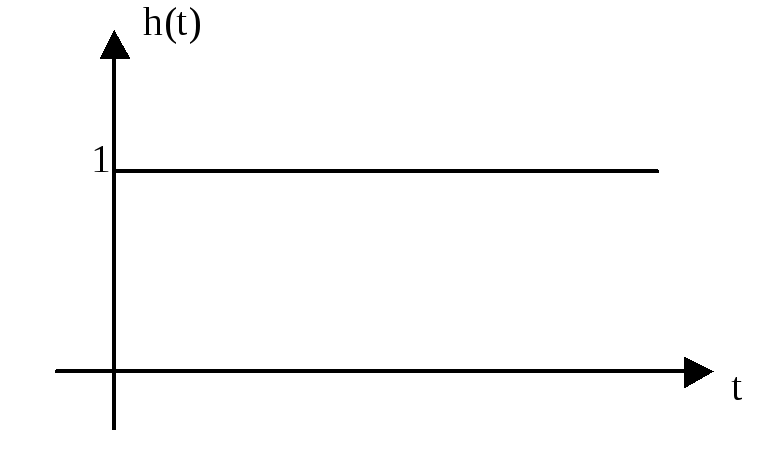
Частотные характеристики:
;
;
;
,
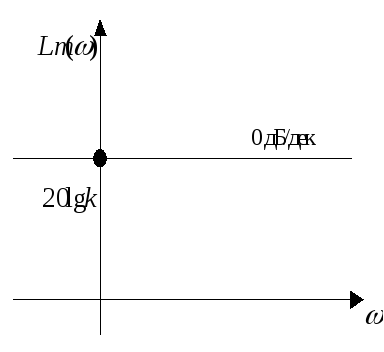
ИНТЕГРИРУЮЩЕЕ ЗВЕНО .
Интегрирующим звеном называется один из простейших динамических элементов или его составная часть, которая имеет передаточную функцию вида
;
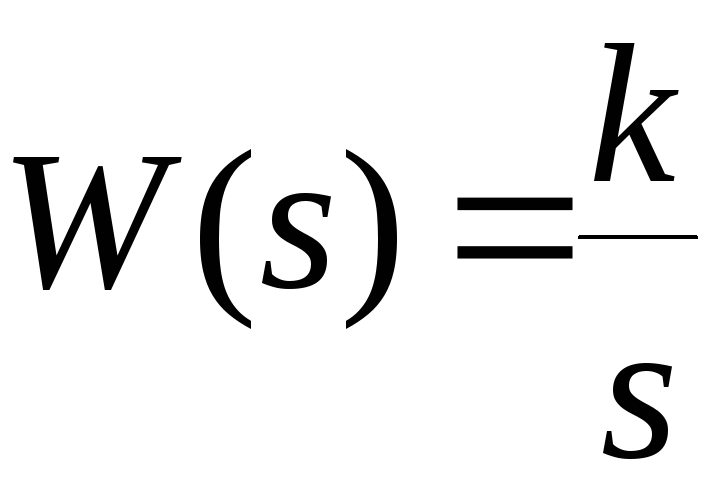(1)
на структурных схемах интегрирующее звено изображается следующим образом
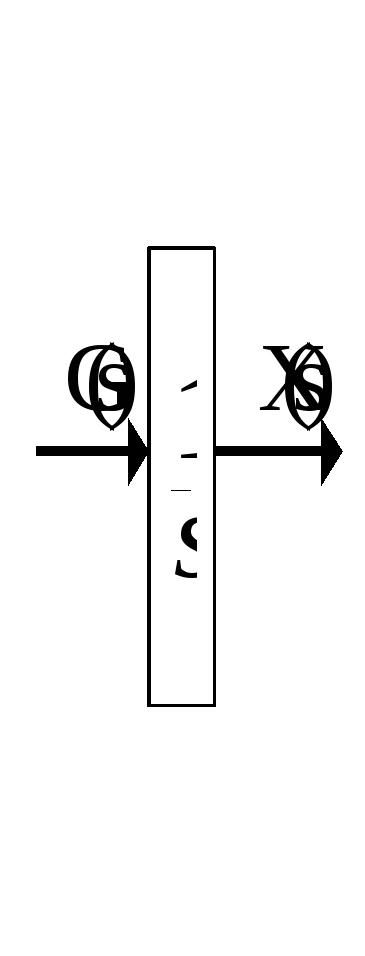
или
при
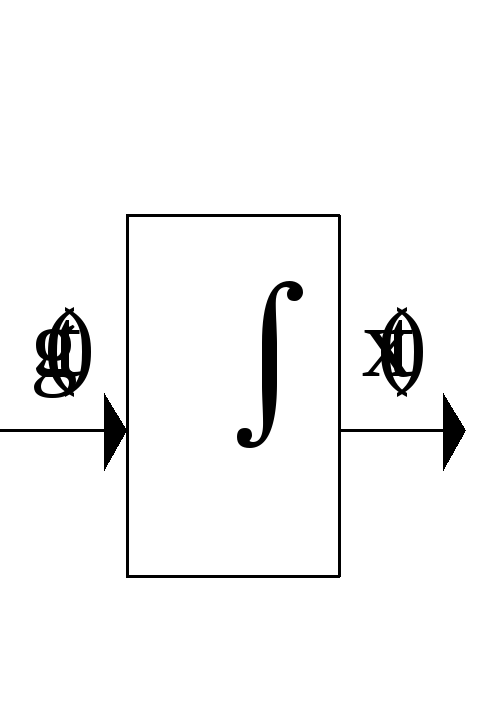
Получим дифференциальное уравнение, являющееся математической моделью интегрирующего звена:
(2)