
- •Характеристики систем автоматического управления и их звеньев.
- •Временные характеристики систем автоматического управления и их звеньев.
- •Характеристики интегрирующего звена.
- •Временные характеристики.
- •Частотные характеристики интегрирующего звена.
- •Апериодическое звено.
- •Правило построения логарифмической амплитудно-частотной характеристики апериодического звена.
- •Колебательное звено.
- •Характеристики колебательного звена.
- •Временные характеристики.
- •Частотные характеристики колебательного звена.
- •Логарифмическая амплитудно-частотная и фазо-частотная характеристики колебательного звена.
- •Дифференцирующее звено первого порядка.
- •Характеристики дифференцирующего звена первого порядка.
- •Временные характеристики.
- •Частотные характеристики.
- •Дифференцирующее звено второго порядка. Математические модели
- •Временные характеристики:
- •Частотные характеристики:
- •Логарифмические частотные
- •Правило построения асимптотических амплитудно-частотных характеристик разомкнутых систем автоматического управления.
- •Об устойчивости.
- •О переходном процессе.
- •О точности системы.
- •Точность систем автоматического управления при гармоническом входном воздействии.
- •Основные виды корректирующих устройств систем автоматического управления.
- •Последовательные корректирующие устройства.
- •Введение производной от ошибки.
- •Увеличение общего коэффициента усиления разомкнутой системы.
- •Введение интеграла от сигнала ошибки системы.
- •Изодромное корректирующее устройство.
- •Параллельные корректирующие устройства.
- •Положительная жесткая обратная связь.
- •Отрицательная жесткая обратная связь.
- •Инерционная жесткая обратная связь.
- •Гибкая обратная связь.
- •Инерционная гибкая обратная связь.
- •Корректирующие устройства по внешнему воздействию. Инвариантность.
- •Корректирующее устройство по задающему воздействию.
- •Корректирующее устройство по возмущению.
- •Краткое сравнение способов коррекции систем автоматического управления при помощи последовательных и параллельных корректирующих устройств.
- •Принцип дуальности управляемости и наблюдаемости.
- •В соответствии с последними уравнениями структурная схема системы имеет вид (сравнить с исходной структурной схемой).
- •Пусть заданна передаточная функция замкнутой системы
- •Или в векторно-матричной форме записи
- •Или в векторно-матричной форме записи
- •Уравнения (7)-(8), а, следовательно, и (9),(10), имеют каноническую форму записи, каноническая форма управляемости.
- •Пример. Задана желаемая передаточная функция разомкнутой системы ,
- •Решение. Желаемая передаточная функция замкнутой системы
- •Пример. Структурная схема объекта управления имеет вид, показанный на рисунке
- •Решение. Введем обозначения
О переходном процессе.
Переходной
процесс в системе автоматического
управления – это
![]() .
.
Качество переходного процесса принято часто характеризовать при помощи следующих величин, называемых показателями качества:
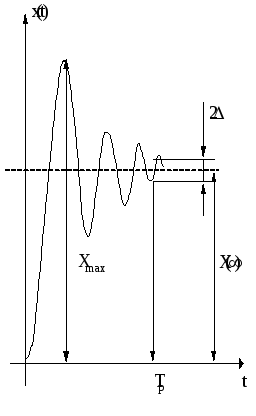
Величина перерегулирования

Статическое отклонение (установившееся значение)
 .
.Времени переходного процесса или времени регулирования: наименьшее значение времени, после которого имеет место неравенство
 ,
,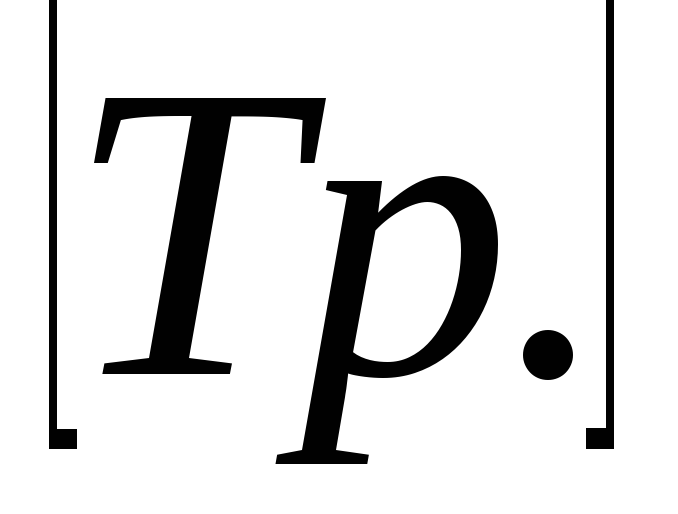 ,
, - заданная малая постоянная величина
(обычно 5% от установившегося значения)
- заданная малая постоянная величина
(обычно 5% от установившегося значения)N – число колебаний регулируемой величины в течении времени переходного процесса
 .
.
О точности системы.
Точность
системы автоматического управления
определяется формулой установившегося
процесса
![]() .
При этом установившаяся ошибка системы
будет
.
При этом установившаяся ошибка системы
будет![]() при
при![]() и характеризует степень близости
выходной переменной к заданному значению
после окончания переходного процесса
в системе.
и характеризует степень близости
выходной переменной к заданному значению
после окончания переходного процесса
в системе.
Переходной
процесс в системе автоматического
управления как правило рассматривают
при подаче на вход системы постоянного
входного воздействия
![]() при нулевых начальных условиях.
при нулевых начальных условиях.
Если
![]() - тогда математической моделью переходного
процесса является переходная функция
замкнутой системы.
- тогда математической моделью переходного
процесса является переходная функция
замкнутой системы.
ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
Пусть структурная схема системы автоматического управления преобразована к расчетной структурной схеме:

Как следует из ранее изложенного для замкнутой системы справедливы следующие соотношения:
 ,
,
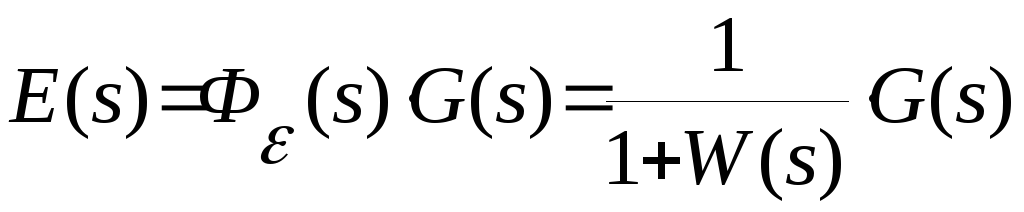 .
.
Изучим временные и частотные характеристики замкнутых систем.
ВРЕМЕННЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ
СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ.
Переходная функция замкнутой системы . Переходная функция замкнутой системы автоматического управления - это ее реакция на единичное входное воздействие:
![]() ;
;
 .
.
Следуя
ранее введенным обозначениям,
![]() - переходная функция системы, а ее
изображение по Лапласу -
- переходная функция системы, а ее
изображение по Лапласу -![]() ,
,![]() .
.
При
![]() , будем иметь
, будем иметь![]() и, следовательно,
и, следовательно,![]() .
Тогда, по передаточной функции разомкнутой
системы управления определим переходную
функцию замкнутой системы:
.
Тогда, по передаточной функции разомкнутой
системы управления определим переходную
функцию замкнутой системы:

 .
.
 .
(1)
.
(1)
Из последнего равенства следует, что для получения переходной функции замкнутой системы управления необходимо:
Преобразовать структурную схему системы к расчетной структурной схеме и получить передаточную функцию разомкнутой системы
 .
.По передаточной функции разомкнутой системы
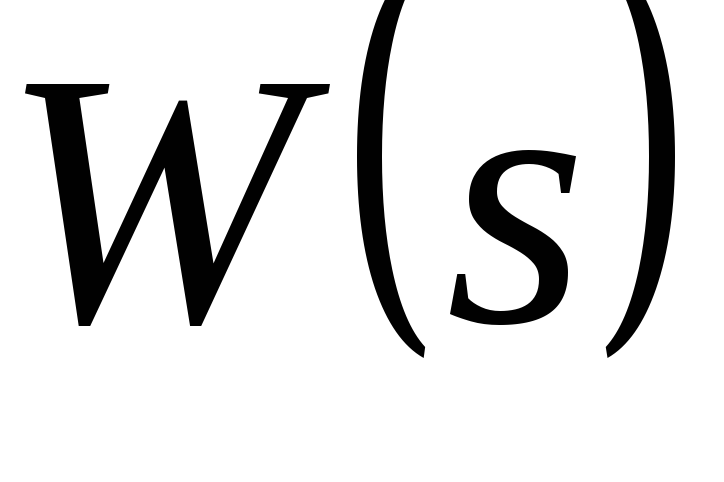 получить передаточную функцию замкнутой
системы
получить передаточную функцию замкнутой
системы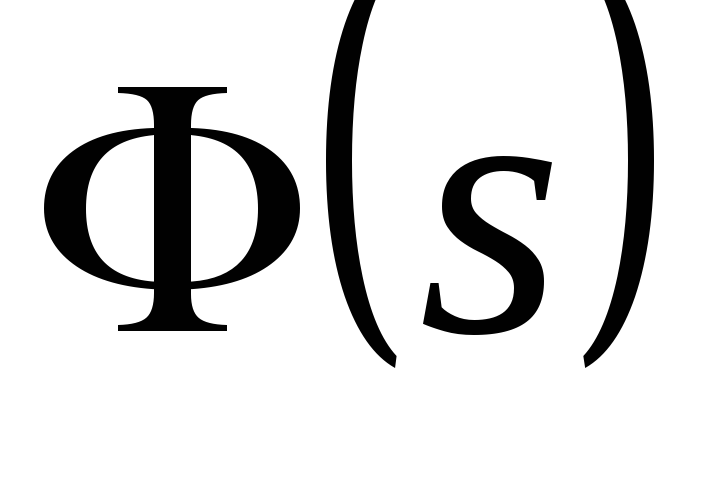 по формуле:
по формуле:
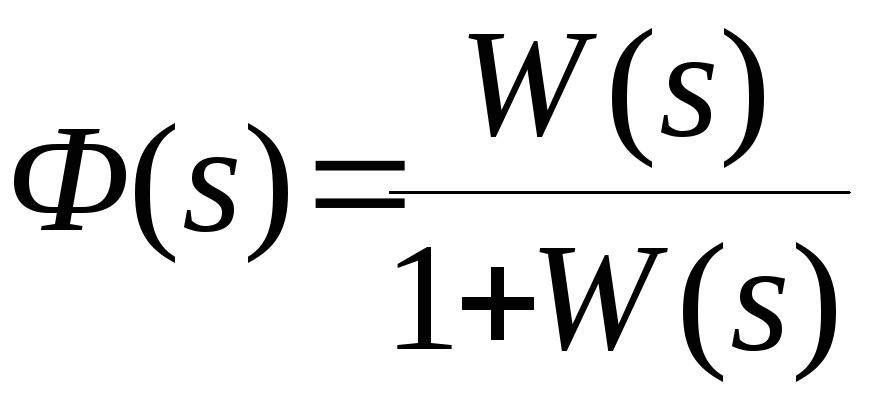 .
.
Выполнить обратное преобразование Лапласа от выражения:
 ,
т. е.
,
т. е. .
.
Не используя равенства (1), можно определить установившееся значение переходной функции замкнутой системы, если воспользоваться «предельными» теоремами преобразования Лапласа. Имеем:
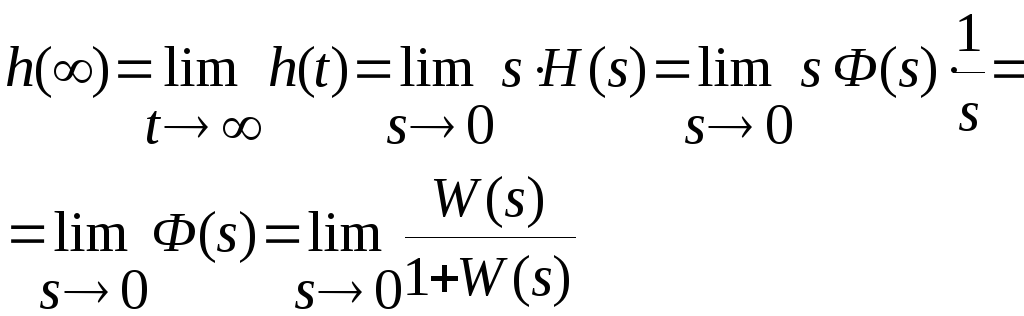 .
.
Следовательно,
 (2)
(2)
Для
замкнутых систем автоматического
управления особый интерес представляет
изучение изменения во времени ошибки
системы
![]() .
Для ошибки системы справедливы следующие
равенства:
.
Для ошибки системы справедливы следующие
равенства:
![]() ;
;
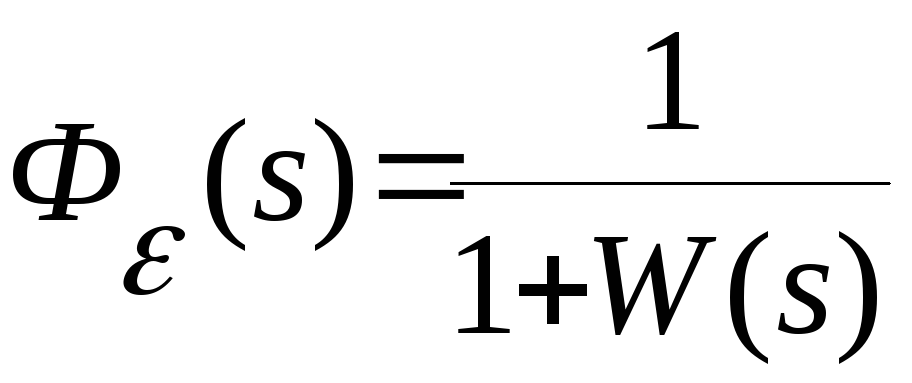 .
.
Таким
образом для
![]() имеем
имеем
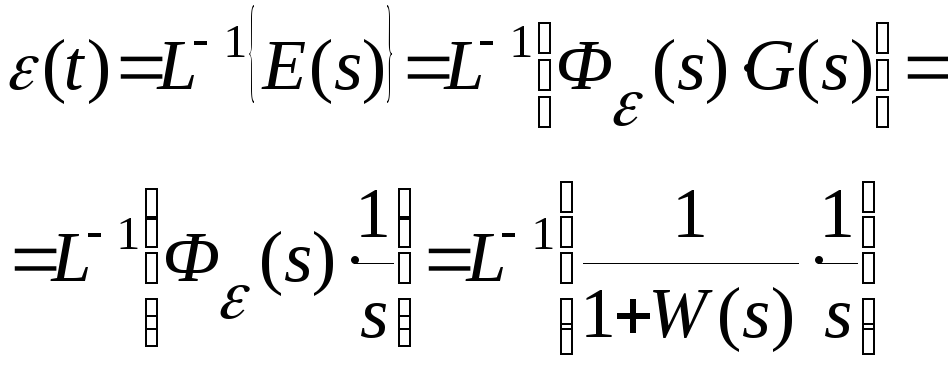
и окончательно
 (3)
(3)
Для того чтобы получить закон изменения во времени ошибки системы необходимо:
Преобразовать структурную схему системы к расчетной структурной схеме и получить передаточную функцию системы
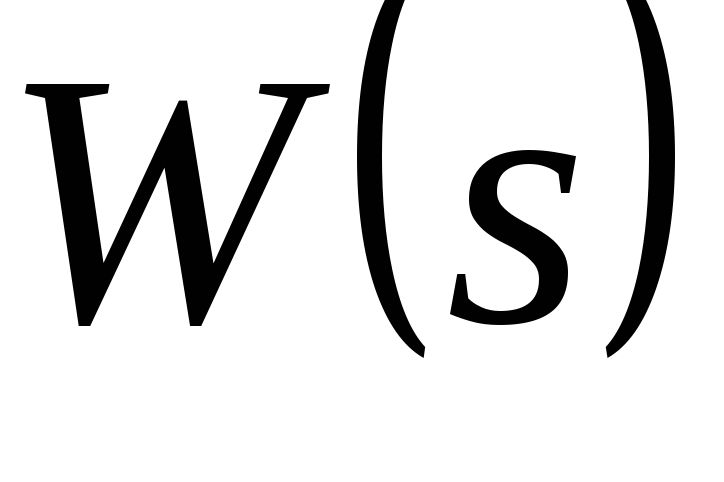 .
.По передаточной функции разомкнутой системы
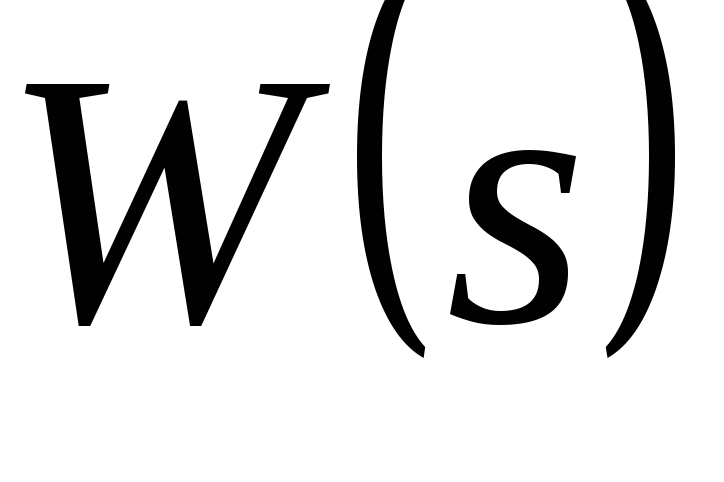 вычислить передаточную функцию замкнутой
системы по ошибке по формуле:
вычислить передаточную функцию замкнутой
системы по ошибке по формуле: .
.Выполнить обратное преобразование Лапласа от выражения
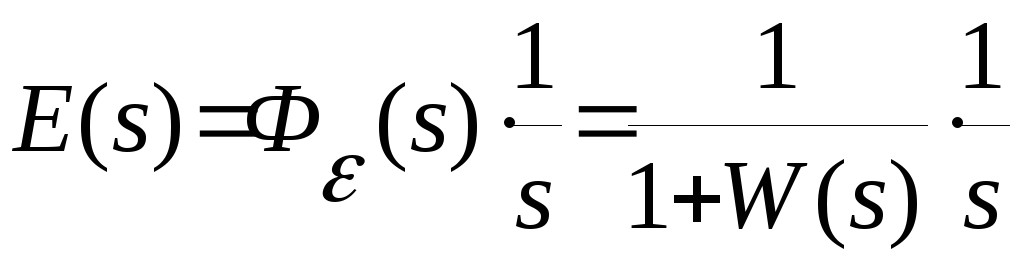 ,
т.е.
,
т.е.
 .
.
Не
используя равенства (3), можно определить
установившееся
![]() и начальное значение ошибки системы,
если воспользоваться «предельными»
теоремами преобразования Лапласа. Имеем
и начальное значение ошибки системы,
если воспользоваться «предельными»
теоремами преобразования Лапласа. Имеем

 (4)
(4)
 ,
,
 .
(5)
.
(5)
Импульсная переходная (весовая) функция замкнутой системы .
Весовой
функцией замкнутой системы автоматического
управления называется функция, описывающая
реакцию замкнутой системы, когда на ее
вход подается
![]() -функция
при нулевых начальных условиях
-функция
при нулевых начальных условиях
![]() ;
;
![]() .
.
Следуя
ранее введенным обозначениям,
![]() – импульсная переходная (весовая)
функция системы, а ее изображение по
Лапласу –
– импульсная переходная (весовая)
функция системы, а ее изображение по
Лапласу –![]() ,
,![]() .
.
При
![]() ,
будем иметь
,
будем иметь![]() и,
следовательно,
и,
следовательно,![]() .
Тогда, по передаточной функции разомкнутой
системы управления определим весовую
(импульсную переходную) функцию замкнутой
системы
.
Тогда, по передаточной функции разомкнутой
системы управления определим весовую
(импульсную переходную) функцию замкнутой
системы
 .
.
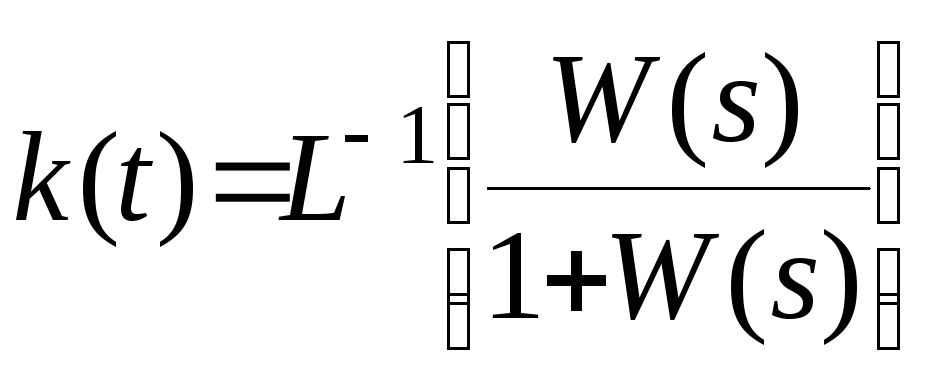 .
(6)
.
(6)
Из полученного равенства следует, что для получения импульсной переходной функции (весовой функции) замкнутой системы необходимо:
Преобразовать структурную схему системы к расчетной структурной схеме и получить передаточную функцию системы
 .
.По передаточной функции разомкнутой системы
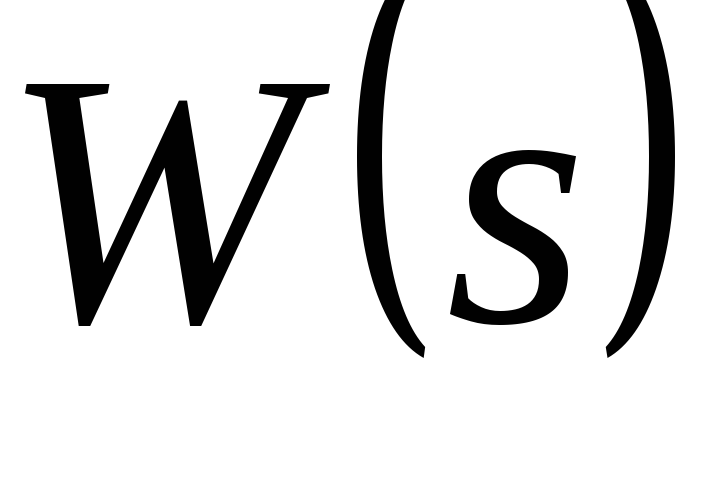 получить передаточную функцию замкнутой
системы
получить передаточную функцию замкнутой
системы по формуле:
по формуле: .
.Выполнить обратное преобразование Лапласа от передаточной функции замкнутой системы
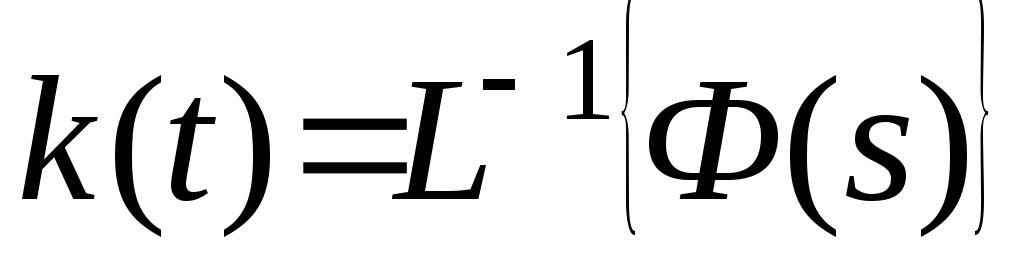 .
.
Для
рассматриваемого случая, чтобы определить
закон изменения во времени ошибки
системы
![]() необходимо
вычислить передаточную функцию замкнутой
системы по ошибке:
необходимо
вычислить передаточную функцию замкнутой
системы по ошибке: ,
а затем найти обратное преобразование
по Лапласу от
,
а затем найти обратное преобразование
по Лапласу от![]() ,
т.е.
,
т.е.![]() .
.
Установившееся
и начальное значения функций
![]() и
и![]() находим
на основании предельных теорем
преобразования Лапласа:
находим
на основании предельных теорем
преобразования Лапласа:
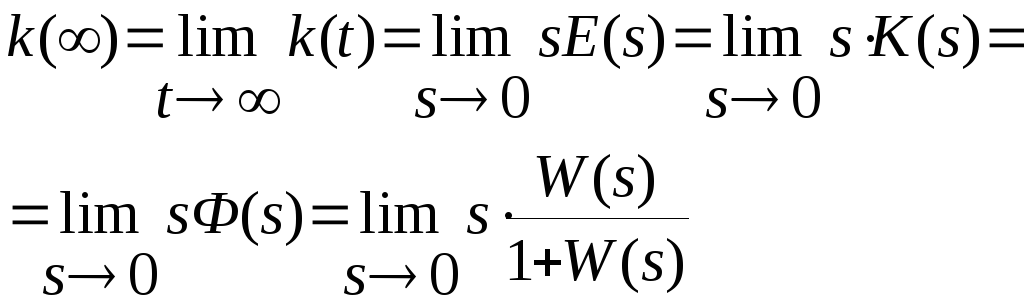 ,
,
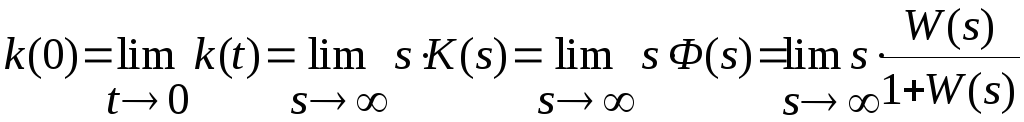 ,
,
 ,
,
 .
.
Установим
связь между импульсной переходной
(весовой) функцией
![]() и переходной функцией
и переходной функцией![]() замкнутой системы. Имеем
замкнутой системы. Имеем
![]() ;
;
![]() ;
;
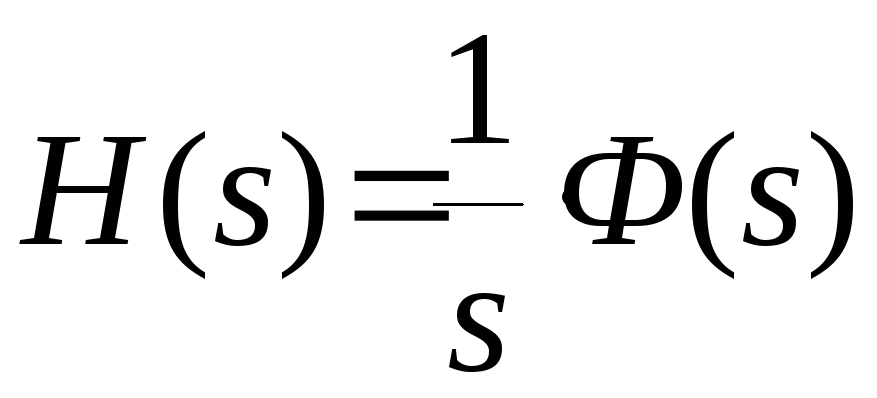 ;
;
![]() ;
;![]()
Следовательно
![]() .
Применим обратное преобразование
Лапласа к обеим частям последнего
равенства
.
Применим обратное преобразование
Лапласа к обеим частям последнего
равенства![]() .
Но так как
.
Но так как![]() ,
то на основании свойства преобразования
Лапласа ( при нулевых начальных условиях
умножение на
,
то на основании свойства преобразования
Лапласа ( при нулевых начальных условиях
умножение на![]() в области изображений соответствует
дифференцированию по
в области изображений соответствует
дифференцированию по![]() в области оригиналов) имеем
в области оригиналов) имеем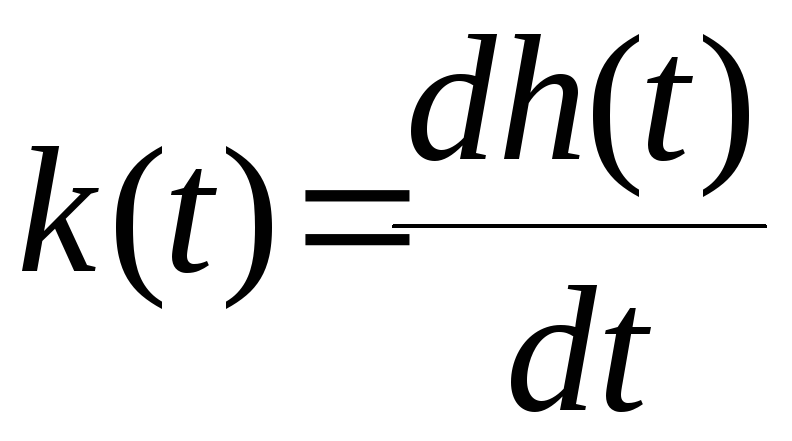 .
.
ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ КОЭФФИЦИЕНТЫ ОШИБОК.
Пусть структурная схема системы автоматического управления приведена к расчетной
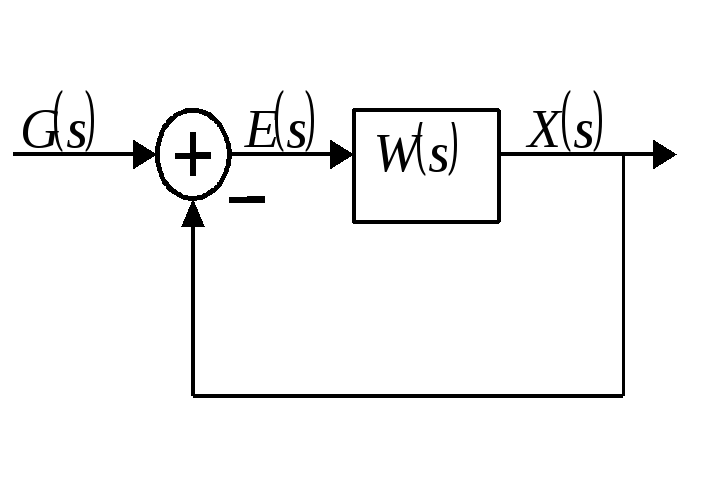
где
![]() - передаточная функция разомкнутой
системы.
- передаточная функция разомкнутой
системы.
Точность системы автоматического управления определяют по установившемуся значению ошибки, т. е. по значению ошибки после окончания переходных процессов в системе
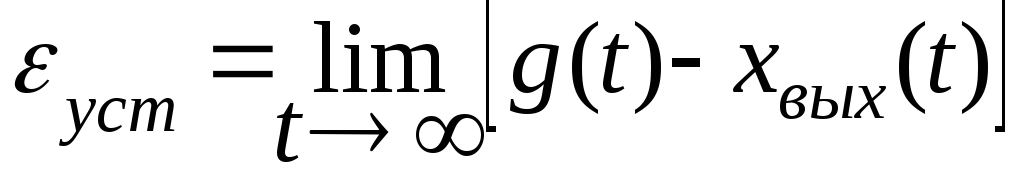 .
.
Значение
![]() зависит:
зависит:
От свойств исследуемой системы управления, которые отражены в принятой математической модели системы, например, параметров
 .
.От входного воздействия, которое отрабатывается исследуемой системой.
Точность системы управления оценивается при типовых входных воздействиях – полиномиальные входные воздействия.
 .
.
ЗАДАЧА: Связать количественную оценку ошибки системы управления в установившемся режиме с передаточной функцией разомкнутой системы – с математической моделью исследуемой системы.
Передаточная функция замкнутой системы по ошибке равна:
 .
.
Из последнего равенства изображение по Лапласу ошибки системы будет иметь вид:
 .
(1)
.
(1)
Для
того, чтобы определить установившееся
значение ошибки системы
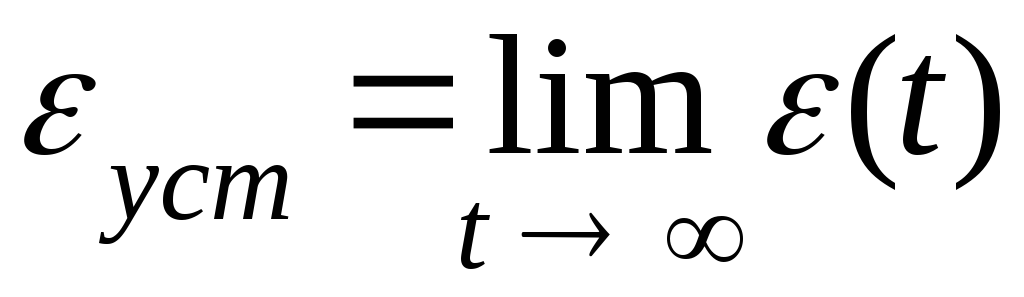 ,
воспользуемся предельным свойством
преобразования Лапласа:
,
воспользуемся предельным свойством
преобразования Лапласа:
 ,
(2)
,
(2)
На
основании равенства (1) можно представить
передаточную функцию по ошибке замкнутой
системы в виде ряда (в окрестности
![]() ):
):
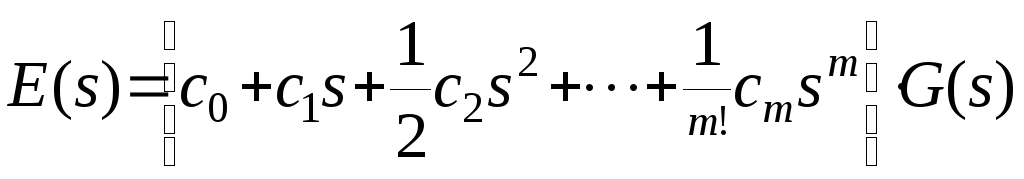 .
(3)
.
(3)
где
числа
![]() ,
,![]() ,
… ,
,
… ,![]() - называются коэффициентами ошибок и
определяются равенствами:
- называются коэффициентами ошибок и
определяются равенствами:
![]() ;
;
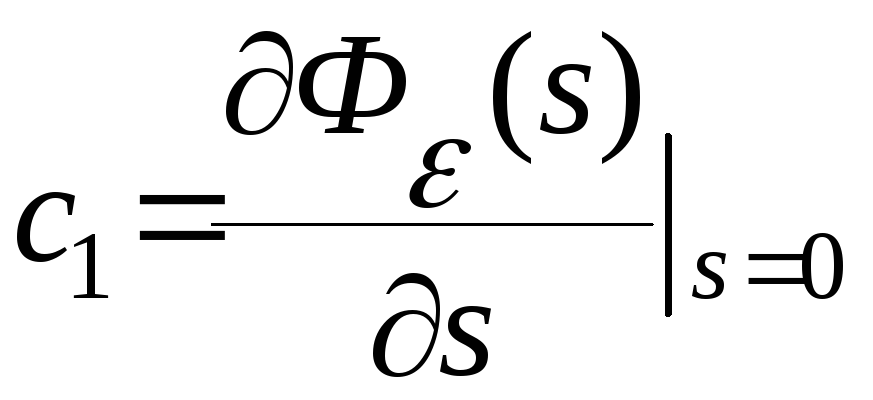 ;
… ;
;
… ; .
.
Подставим (3) в (2), получаем:
 .
.
Исследуем
изменение величины
![]() от вида входного воздействия и
коэффициентов передаточной функции
разомкнутой системы – параметров
математической модели исследуемой
системы управления.
от вида входного воздействия и
коэффициентов передаточной функции
разомкнутой системы – параметров
математической модели исследуемой
системы управления.
Случай I.
Единичное, входное воздействие:
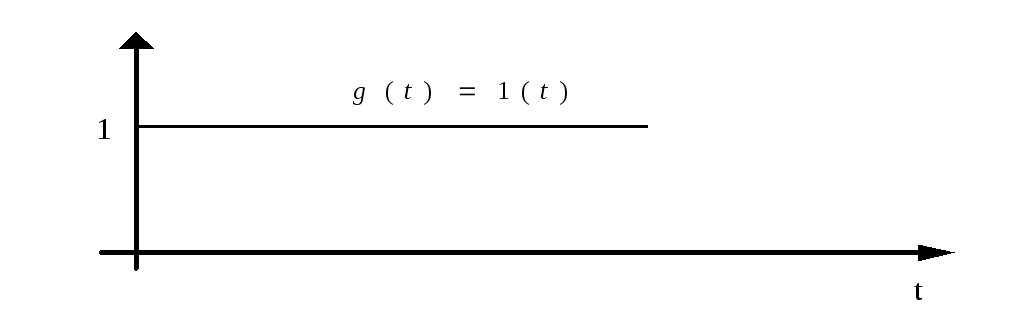
![]() ;
;
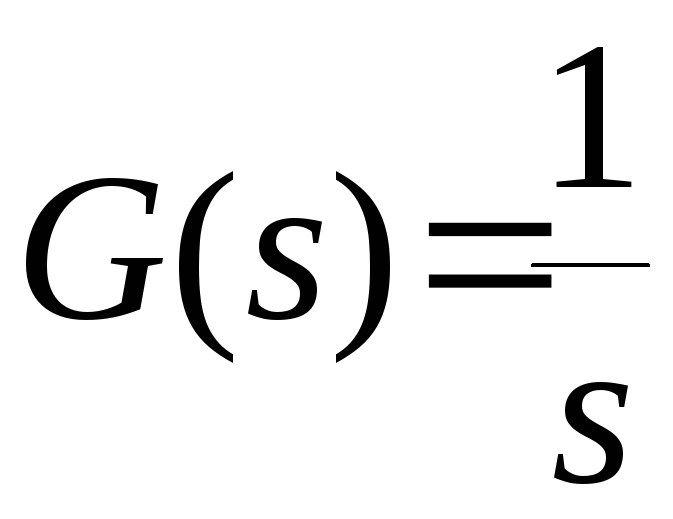 .
.
I.1. Передаточная функция разомкнутой системы имеет вид:

Тогда передаточная функция замкнутой системы по ошибке запишется в виде
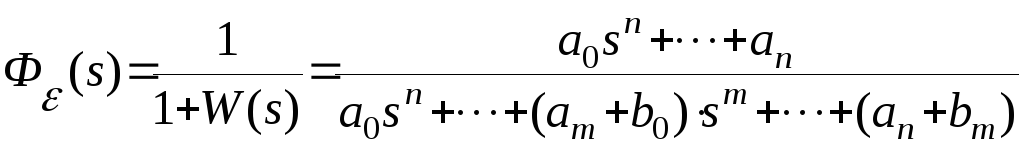 .
.
Предполагаем, что замкнутая система асимптотически устойчива, тогда установившееся значение ошибки в замкнутой системе будет
 .
.
С другой стороны
 .
.
Следовательно
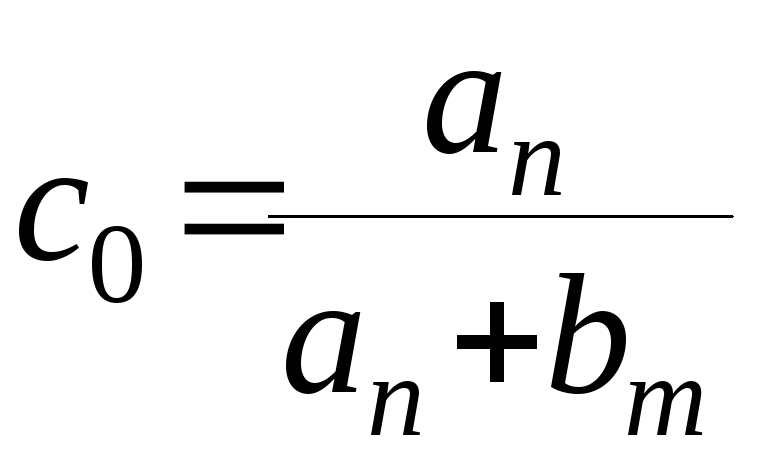 .
Обозначим через
.
Обозначим через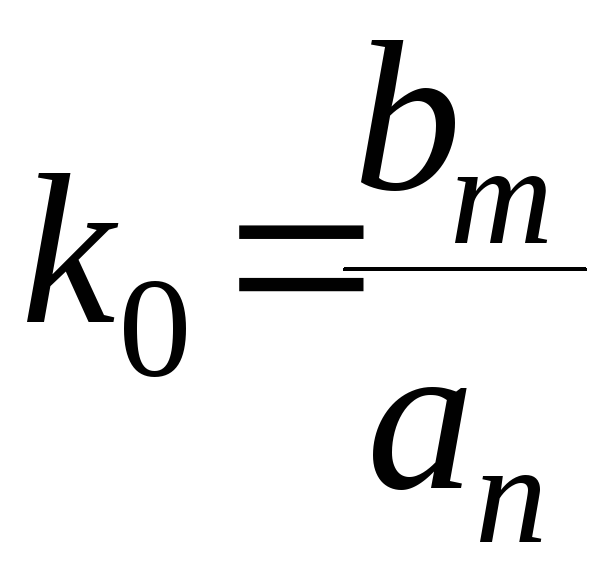 - это коэффициент усиления разомкнутой
системы, тогда
- это коэффициент усиления разомкнутой
системы, тогда .
.![]() - коэффициент статической ошибки, или
ошибки позиционирования системы.
- коэффициент статической ошибки, или
ошибки позиционирования системы.
ВЫВОД. Если передаточная функция разомкнутой системы имеет вид
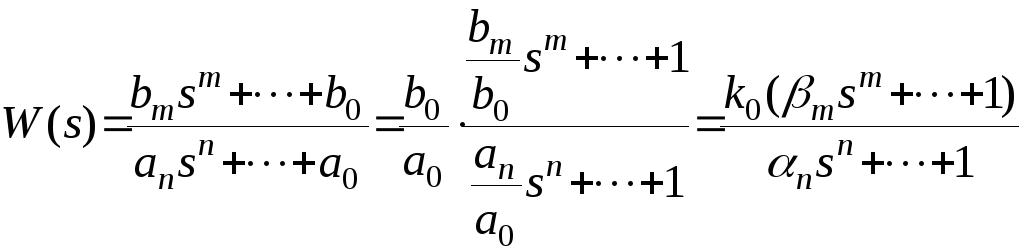 ,
,
то
установившееся значение ошибки в
замкнутой
системе будет определяться из соотношения:
 .
Такие системы автоматического управления
называютсястатическими.
В статических системах для уменьшения
ошибки в системе в установившемся режиме
повышают коэффициент усиления разомкнутой
системы (
.
Такие системы автоматического управления
называютсястатическими.
В статических системах для уменьшения
ошибки в системе в установившемся режиме
повышают коэффициент усиления разомкнутой
системы (![]()
![]()
![]() ).
Но при увеличении коэффициента усиления
система может потерять устойчивость.
).
Но при увеличении коэффициента усиления
система может потерять устойчивость.
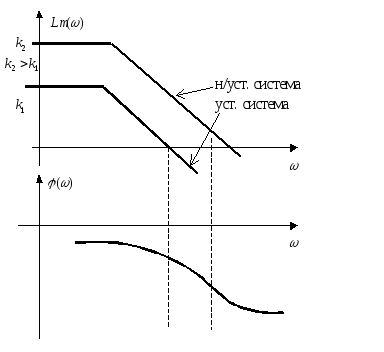
Особенность
логарифмических характеристик статических
систем: первая асимптота логарифмической
амплитудно-частотной характеристики
имеет наклон
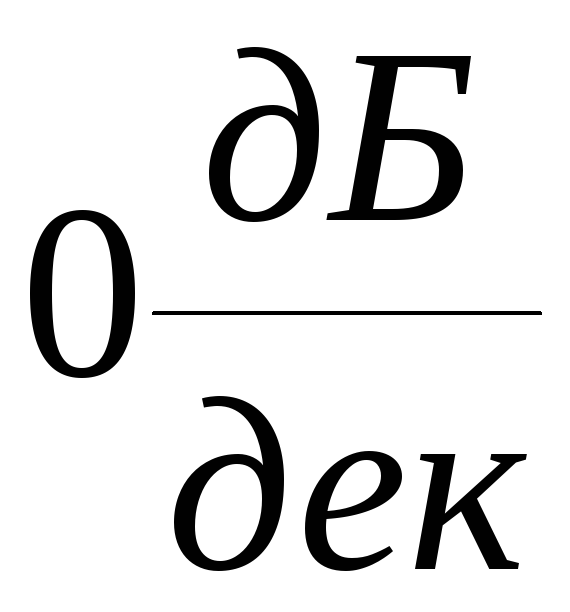 .
.
II.2.
В знаменателе передаточной функции
разомкнутой системы коэффициент
![]() .
.
В этом случае передаточная функция разомкнутой системы принимает вид:
 .
.
С учетом полученного равенства передаточная функция замкнутой системы по ошибке имеет вид
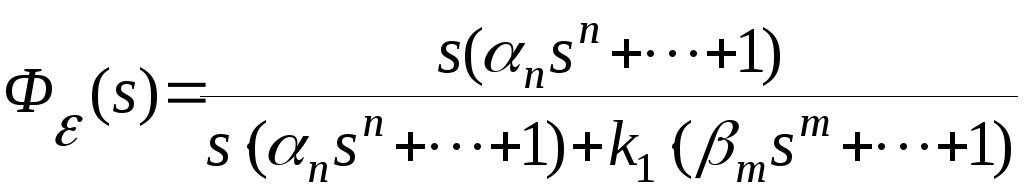 .
.
Установившееся значение ошибки в замкнутой системе будет равно
 .
.
Следовательно,
![]() и в системе, в установившемся режиме,
нет статической ошибки. Система
автоматического управления с передаточной
функцией
и в системе, в установившемся режиме,
нет статической ошибки. Система
автоматического управления с передаточной
функцией
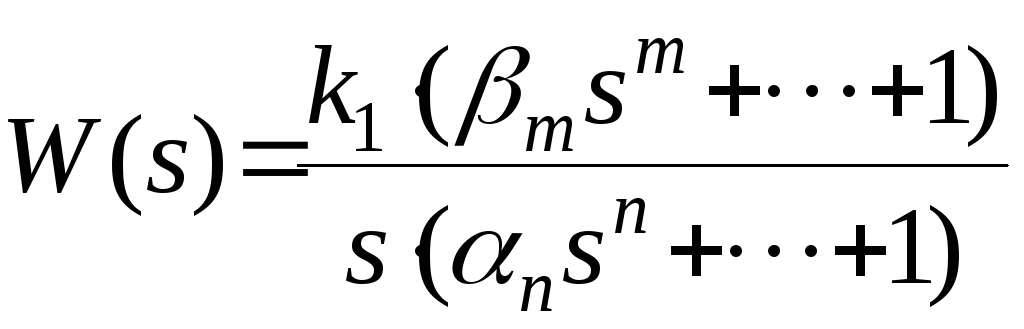
обладает
АСТАТИЗМОМ первого порядка. Характерно
для логарифмических амплитудно-частотных
характеристик разомкнутых систем:
первая асимптота имеет наклон
 .
.

Если передаточная функция разомкнутой системы автоматического управления имеет вид
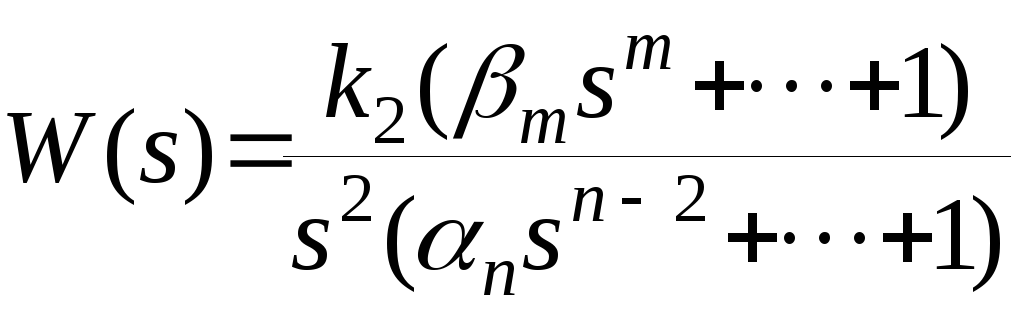 ,
,
то
говорят, что система обладает астатизмом
второго порядка. Для систем управления
с астатизмом второго порядка
![]() ;
;![]() .
.
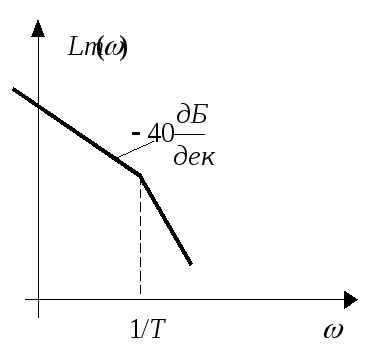
Характерно
для логарифмических амплитудно-частотных
характеристик разомкнутых систем:
первая асимптота имеет наклон
 .
.
Случай II.
![]() ;
; 
II.
1. Статическая система
 .
Передаточная функция замкнутой системы
по ошибке
.
Передаточная функция замкнутой системы
по ошибке
 .
.
Ошибка замкнутой системы автоматического управления в установившемся режиме будет
 .
.
ВЫВОД.
В статических системах при входном
воздействии
![]() ошибка
ошибка![]() неограниченно возрастает; статические
системы не могут отработать такой
входной сигнал.
неограниченно возрастает; статические
системы не могут отработать такой
входной сигнал.
II.2. Система с астатизмом первого порядка
 .
.
Передаточная функция замкнутой системы по ошибке
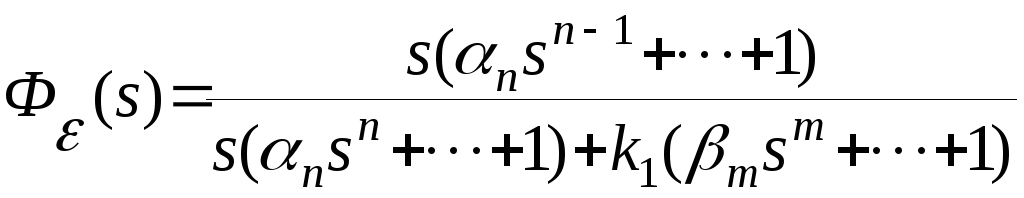
Ошибка замкнутой системы автоматического управления в установившемся режиме будет
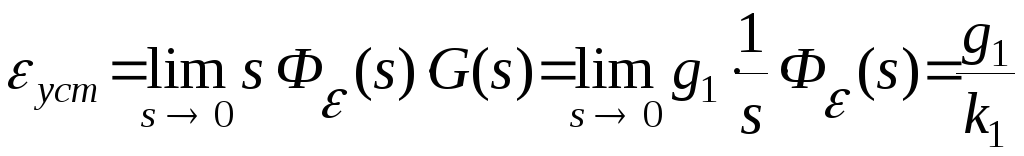 .
.
С другой стороны

![]() ,
т. к.
,
т. к.
![]() -
по условию система с астатизмом первого
порядка. Следовательно
-
по условию система с астатизмом первого
порядка. Следовательно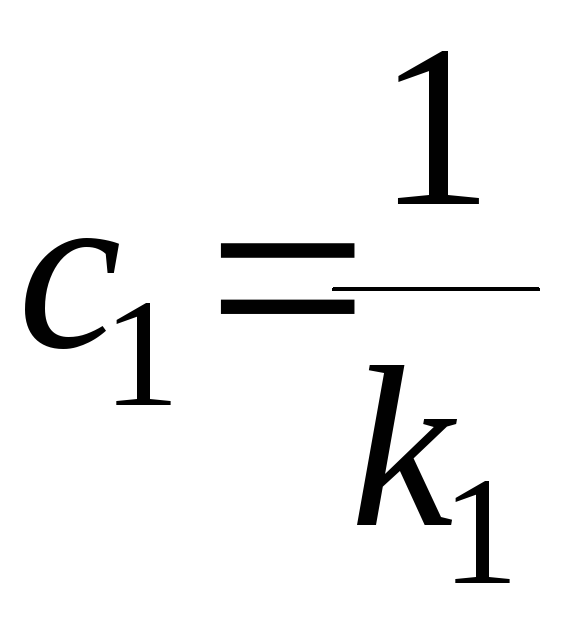 .
Для уменьшения ошибки в системах
автоматического управления, обладающих
астатизмом первого порядка, при входном
воздействии
.
Для уменьшения ошибки в системах
автоматического управления, обладающих
астатизмом первого порядка, при входном
воздействии![]() следует увеличивать коэффициент усиления
разомкнутой системы
следует увеличивать коэффициент усиления
разомкнутой системы![]() ,
но это может привести к потере устойчивости
замкнутой системы. Коэффициент
,
но это может привести к потере устойчивости
замкнутой системы. Коэффициент![]() называется коэффициентом ошибки системы
по скорости.
называется коэффициентом ошибки системы
по скорости.
II.3 Система автоматического управления с астатизмом второго порядка
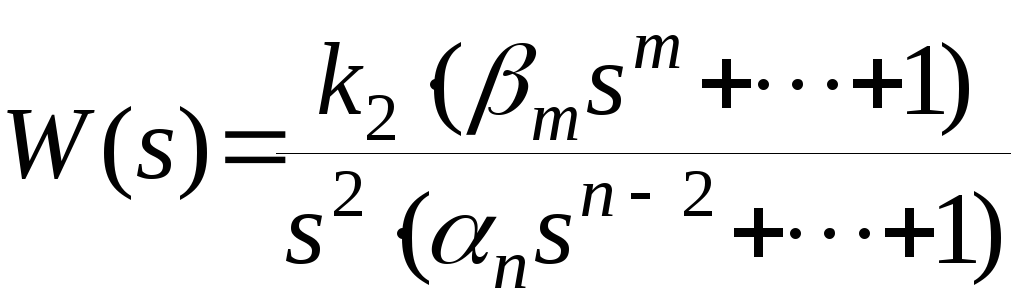 .
.
Передаточная функция замкнутой системы по ошибке
 .
.
Установившееся значение ошибки
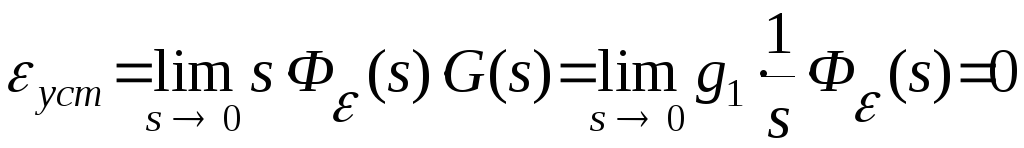 .
.
тн7С другой стороны
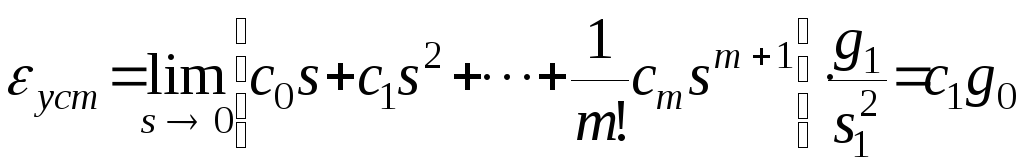 .
.
Сравнивая
два последних равенства, приходим к
выводу, что в системах автоматического
управления, обладающих астатизмом
второго порядка, коэффициент скоростной
ошибки равен нулю, т.е.
![]() .
.
Случай III.
![]() ;
; 
III.1
Статическая система
 .
Передаточная функция замкнутой системы
по ошибке
.
Передаточная функция замкнутой системы
по ошибке
 .
.
Ошибка замкнутой системы автоматического управления в установившемся режиме будет
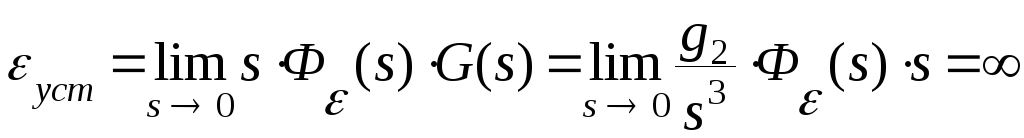 .
.
ВЫВОД.
В статических системах при входном
воздействии
![]() ошибка
ошибка![]() неограниченно возрастает. Такого вида
входное воздействие статическая система
отработатьне
может.
неограниченно возрастает. Такого вида
входное воздействие статическая система
отработатьне
может.
III.2 Система с астатизмом первого порядка
 .
.
Передаточная функция замкнутой системы по ошибке
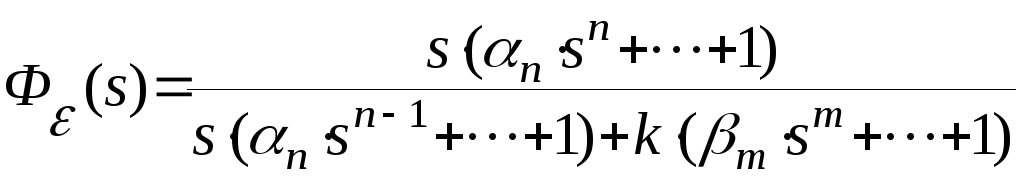 .
.
Ошибка замкнутой системы автоматического управления в установившемся режиме будет
 .
.
ВЫВОД.
В системах автоматического управления,
обладающих астатизмом первого порядка,
при входном воздействии
![]() ошибка
ошибка![]() неограниченно возрастает. Такого вида
входное воздействие система с астатизмом
первого порядка отработатьне
может.
неограниченно возрастает. Такого вида
входное воздействие система с астатизмом
первого порядка отработатьне
может.
III.3 Система автоматического управления с астатизмом второго порядка
 .
.
Передаточная функция замкнутой системы по ошибке
 .
.
Ошибка замкнутой системы в установившемся режиме будет

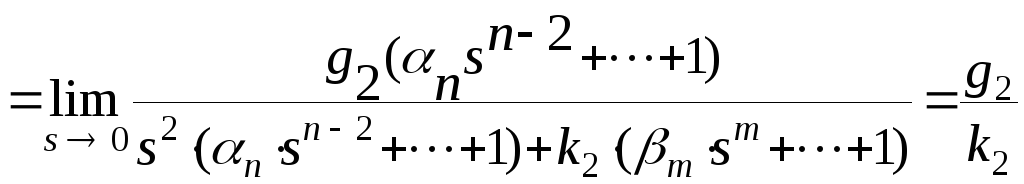 .
.
С другой стороны
 .
.
Сравнивая
два последних равенства, приходим к
выводу, что в системах автоматического
управления, обладающих астатизмом
второго порядка, коэффициент ошибки по
ускорению
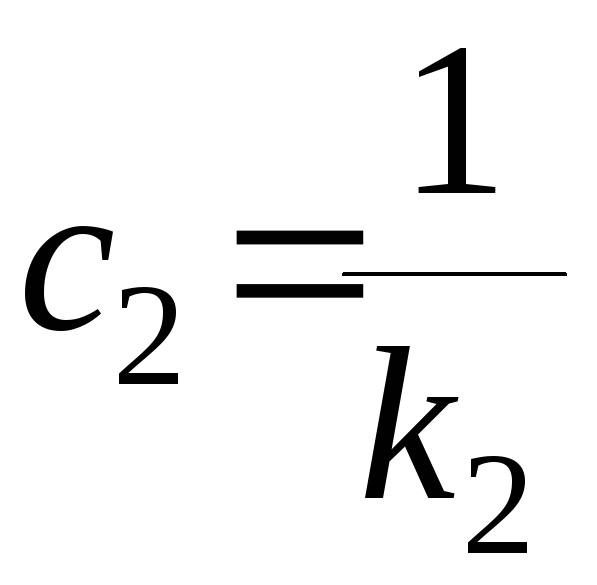 .
.
Для
уменьшения ошибки в системах автоматического
управления, обладающих астатизмом
второго порядка при входном воздействии
![]() следует увеличивать коэффициент усиления
разомкнутой системы
следует увеличивать коэффициент усиления
разомкнутой системы![]() ,
но это так же может привести к потери
устойчивости замкнутой системы.
,
но это так же может привести к потери
устойчивости замкнутой системы.
Пример. Задана передаточная функция замкнутой системы
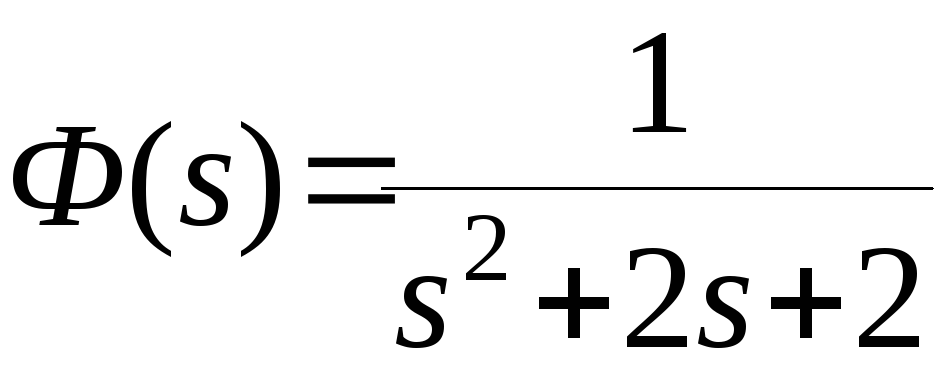 .
.
Найти коэффициенты ошибки системы.
Решение.
Передаточная функция по ошибке связана
с передаточной функцией замкнутой
системы равенством:
![]()
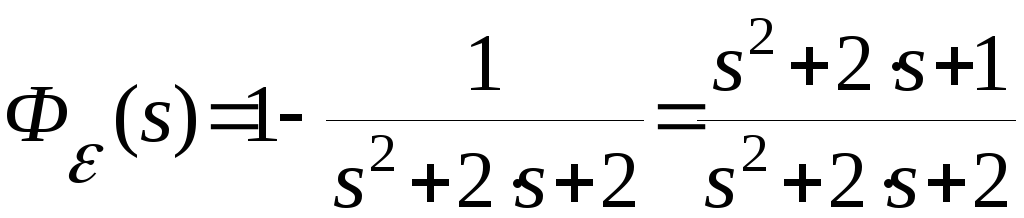 .
.
В результате деления числитель на знаменатель получаем
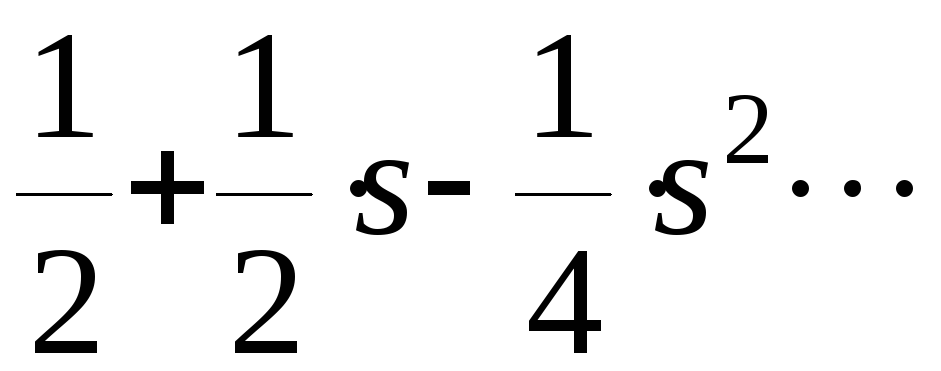
Следовательно,
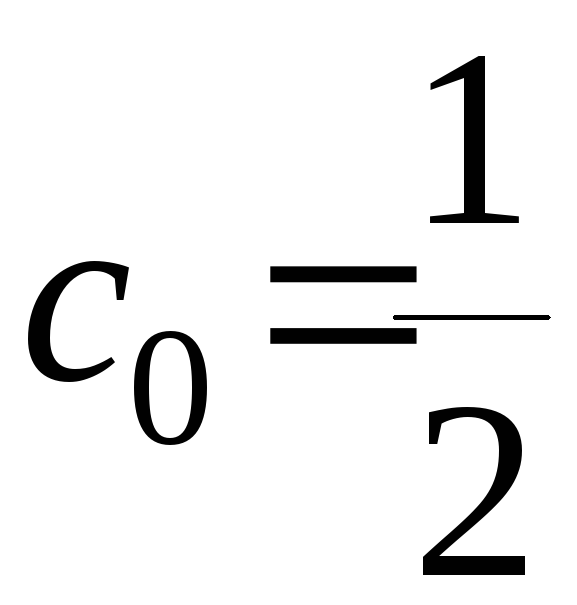 ,
, ,
,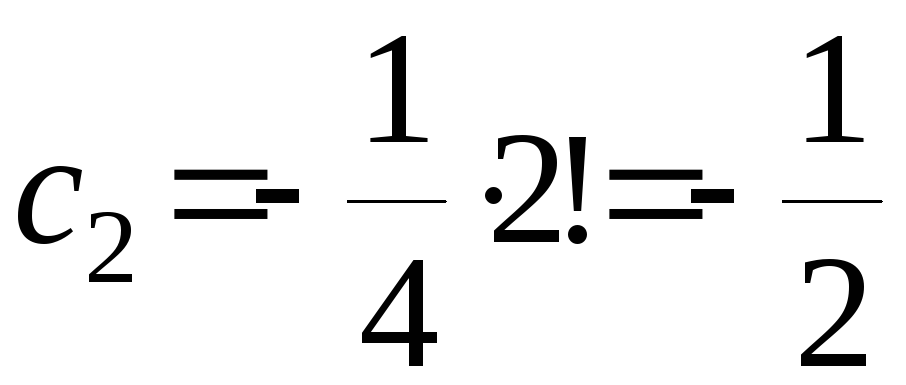 .
.
