
- •Характеристики систем автоматического управления и их звеньев.
- •Временные характеристики систем автоматического управления и их звеньев.
- •Характеристики интегрирующего звена.
- •Временные характеристики.
- •Частотные характеристики интегрирующего звена.
- •Апериодическое звено.
- •Правило построения логарифмической амплитудно-частотной характеристики апериодического звена.
- •Колебательное звено.
- •Характеристики колебательного звена.
- •Временные характеристики.
- •Частотные характеристики колебательного звена.
- •Логарифмическая амплитудно-частотная и фазо-частотная характеристики колебательного звена.
- •Дифференцирующее звено первого порядка.
- •Характеристики дифференцирующего звена первого порядка.
- •Временные характеристики.
- •Частотные характеристики.
- •Дифференцирующее звено второго порядка. Математические модели
- •Временные характеристики:
- •Частотные характеристики:
- •Логарифмические частотные
- •Правило построения асимптотических амплитудно-частотных характеристик разомкнутых систем автоматического управления.
- •Об устойчивости.
- •О переходном процессе.
- •О точности системы.
- •Точность систем автоматического управления при гармоническом входном воздействии.
- •Основные виды корректирующих устройств систем автоматического управления.
- •Последовательные корректирующие устройства.
- •Введение производной от ошибки.
- •Увеличение общего коэффициента усиления разомкнутой системы.
- •Введение интеграла от сигнала ошибки системы.
- •Изодромное корректирующее устройство.
- •Параллельные корректирующие устройства.
- •Положительная жесткая обратная связь.
- •Отрицательная жесткая обратная связь.
- •Инерционная жесткая обратная связь.
- •Гибкая обратная связь.
- •Инерционная гибкая обратная связь.
- •Корректирующие устройства по внешнему воздействию. Инвариантность.
- •Корректирующее устройство по задающему воздействию.
- •Корректирующее устройство по возмущению.
- •Краткое сравнение способов коррекции систем автоматического управления при помощи последовательных и параллельных корректирующих устройств.
- •Принцип дуальности управляемости и наблюдаемости.
- •В соответствии с последними уравнениями структурная схема системы имеет вид (сравнить с исходной структурной схемой).
- •Пусть заданна передаточная функция замкнутой системы
- •Или в векторно-матричной форме записи
- •Или в векторно-матричной форме записи
- •Уравнения (7)-(8), а, следовательно, и (9),(10), имеют каноническую форму записи, каноническая форма управляемости.
- •Пример. Задана желаемая передаточная функция разомкнутой системы ,
- •Решение. Желаемая передаточная функция замкнутой системы
- •Пример. Структурная схема объекта управления имеет вид, показанный на рисунке
- •Решение. Введем обозначения
Правило построения асимптотических амплитудно-частотных характеристик разомкнутых систем автоматического управления.
Получить передаточную функцию разомкнутой системы автоматического управления:
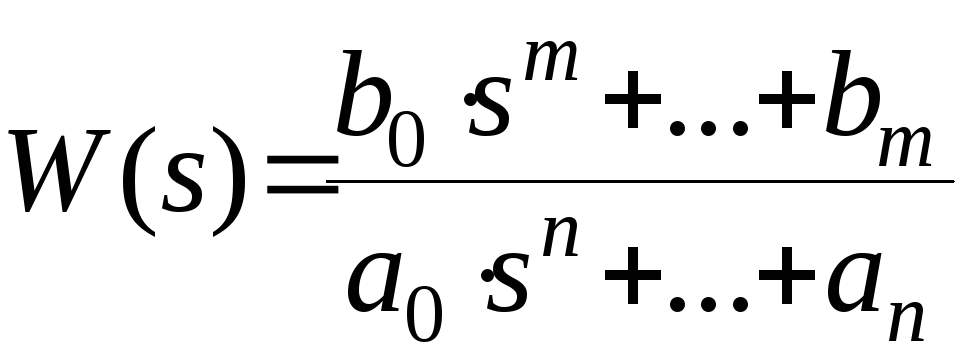
Представить передаточную функцию
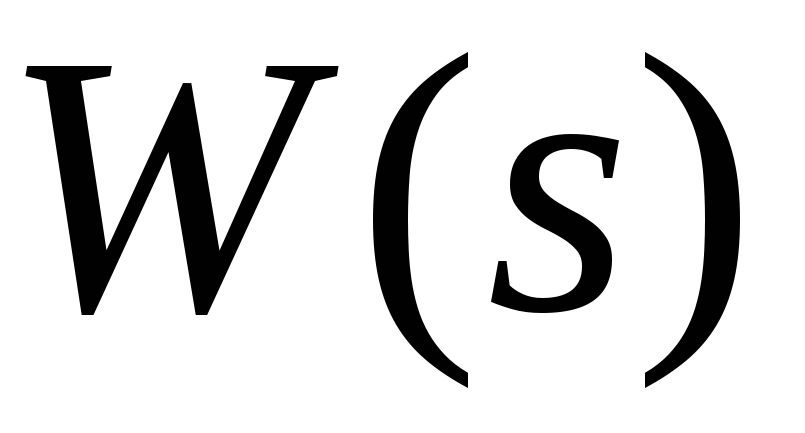 разомкнутой системы управления в виде
разомкнутой системы управления в виде
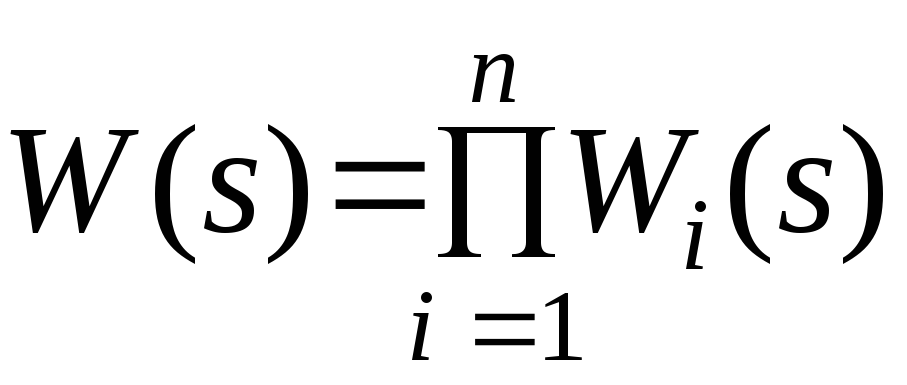 ,
,
где
![]() - передаточная функция
- передаточная функция![]() -го
элементарного звена.
-го
элементарного звена.
Определить сопрягающие частоты и значение
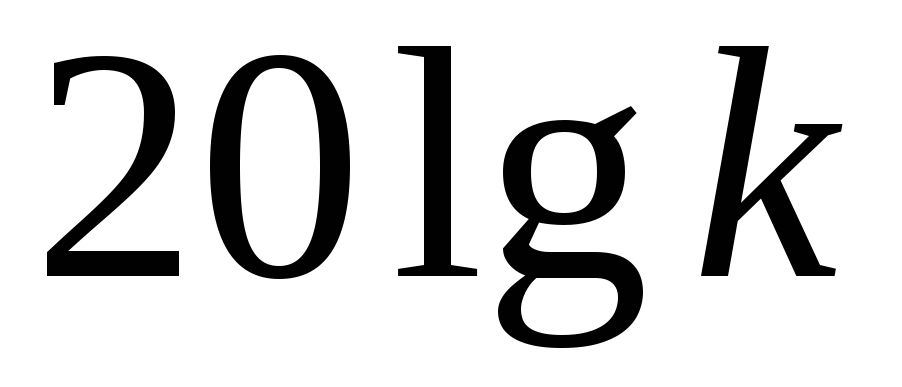 и наносят значения сопрягающих частот
на ось
и наносят значения сопрягающих частот
на ось и отмечают точку с координатами
и отмечают точку с координатами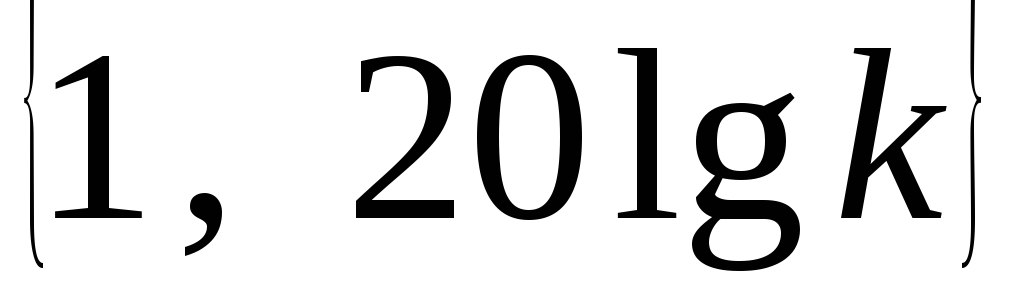 .
.Через точку с координатами
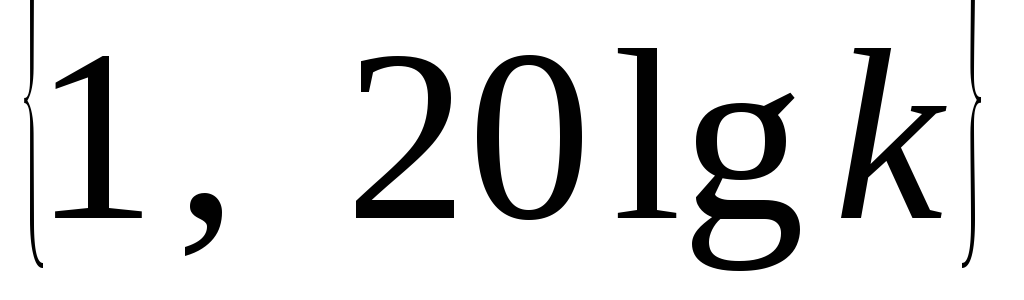 проводят первую асимптоту с наклоном
проводят первую асимптоту с наклоном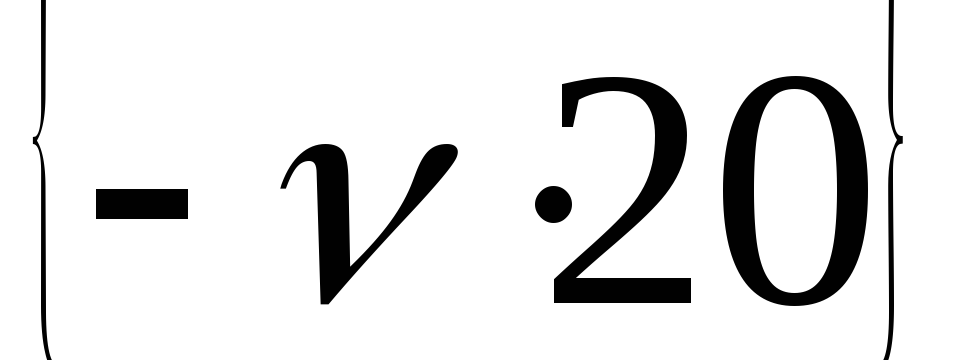 дБ/дек до первой сопрягающей частоты.
дБ/дек до первой сопрягающей частоты.Проводят вторую асимптоту от правого конца первой до второй сопрягающей частоты. Её наклон изменяется на
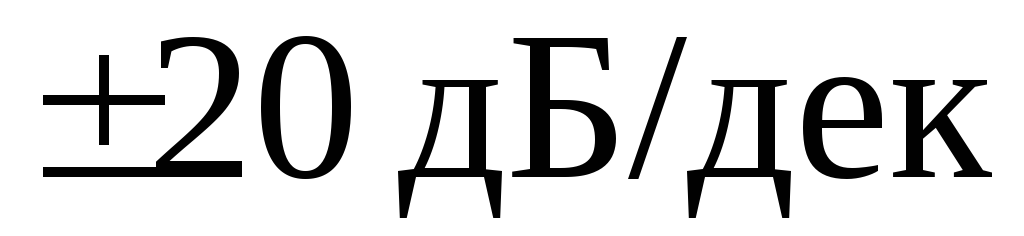 или
на
или
на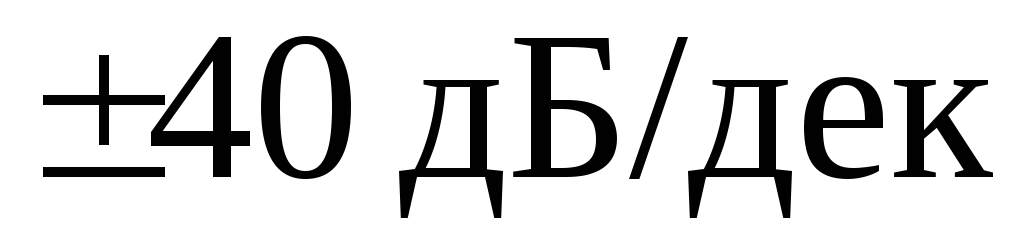 в
зависимости от того, является ли
сопрягающая частота – сопрягающей
частотой апериодического, дифференцирующего
звена первого порядка и т.п.
в
зависимости от того, является ли
сопрягающая частота – сопрягающей
частотой апериодического, дифференцирующего
звена первого порядка и т.п.Строят каждую последующую асимптоту аналогично второй. Изменение наклона
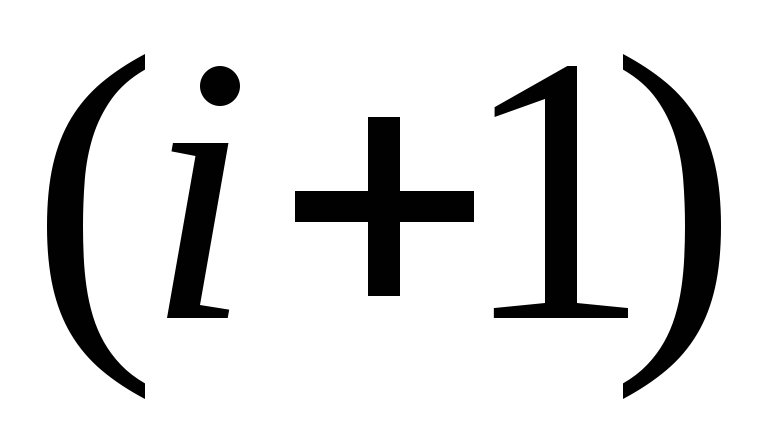 -ой
асимптоты зависит от того, сопрягающей
частотой какого элементарного звена
является
-ой
асимптоты зависит от того, сопрягающей
частотой какого элементарного звена
является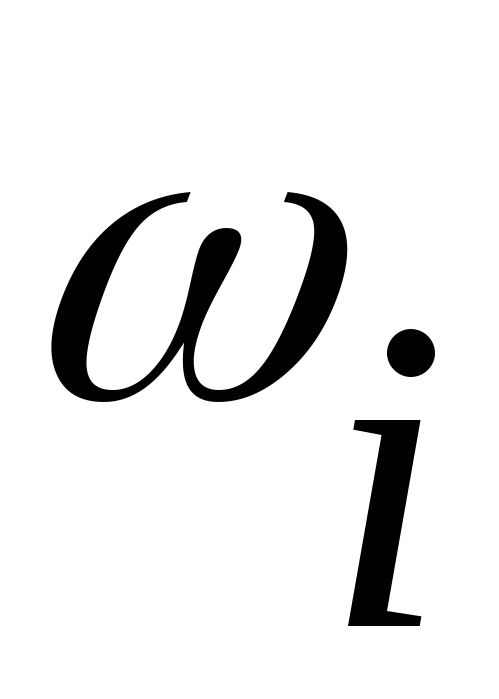 .
.
Если
какая-либо сопрягающая частота является
кратной и ее кратность равна
![]() (имеется
(имеется![]() одинаковых элементарных звеньев), то
изменение наклона при этой частоте в
одинаковых элементарных звеньев), то
изменение наклона при этой частоте в![]() раз больше, чем при соответствующей
простой частоте.
раз больше, чем при соответствующей
простой частоте.
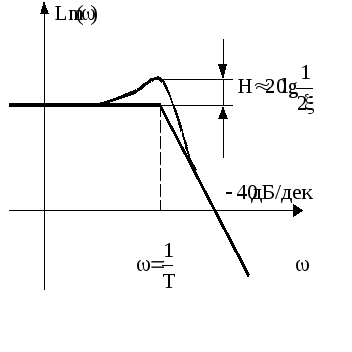
Для колебательных звеньев необходимо выполнить поправки в соответствии с графиками, шаблонами и т.п., можно по формуле:
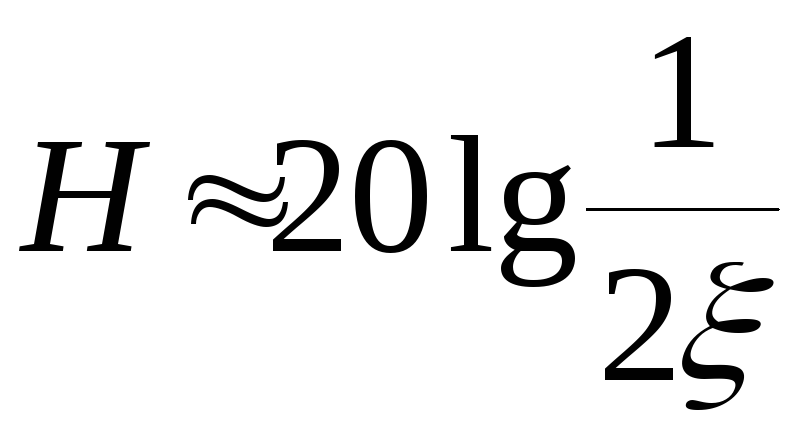
КАЧЕСТВО ПРОЦЕССОВ УПРАВЛЕНИЕ.
Одной из основных задач теории автоматического управления является изучение характерных особенностей процессов, которые протекают в исследуемой системе. Это осуществляется средствами математики.
Каждую систему управления можно описать системой дифференциальных уравнений - это математическая модель системы в форме дифференциальных уравнений.
Математической моделью процессов в исследуемой системе является решение дифференциальных уравнений, которые описывают динамические процессы в исследуемой системе. Это решение (для выходной переменной) имеет вид
![]() ,
,
где
![]() -собственное
движение системы, определяется общим
решением соответствующего однородного
уравнения;
-собственное
движение системы, определяется общим
решением соответствующего однородного
уравнения;![]() -вынужденное
движение, определяется частным решением
неоднородного уравнения и зависит от
вида правой части уравнения.
-вынужденное
движение, определяется частным решением
неоднородного уравнения и зависит от
вида правой части уравнения.
С точки зрения протекания процессов в системе, требования к процессам делятся на три группы:
1.Устойчивость системы
2.Качество переходного процесса
3.Точность отработки заданного входного воздействия
С точки зрения теории автоматического управления
![]() -
в основном определяет характер переходных
процессов в исследуемой системе;
характеризует устойчивость системы.
-
в основном определяет характер переходных
процессов в исследуемой системе;
характеризует устойчивость системы.
![]() -
установившиеся процессы в системе. На
эту составляющую накладывается переходной
процесс, влияние которого становится
незначительным по истечении времени.
-
установившиеся процессы в системе. На
эту составляющую накладывается переходной
процесс, влияние которого становится
незначительным по истечении времени.
Об устойчивости.
Под устойчивостью системы понимают ее способность возвращаться в состояние равновесия после снятия возмущающих факторов, действующих на систему. Если система неустойчива, то под воздействием внешних возмущений или после их снятия, она переходит из одного состояния равновесия в другие состояния равновесия (или остается в исходном состоянии). Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.
Устойчивость
системы автоматического управления
затухание процессов в системе:
![]() при
при![]()
О качестве процессов управления, о неточности отработки заданного входного воздействия речь может идти толь для устойчивых систем.
