
- •Характеристики систем автоматического управления и их звеньев.
- •Временные характеристики систем автоматического управления и их звеньев.
- •Характеристики интегрирующего звена.
- •Временные характеристики.
- •Частотные характеристики интегрирующего звена.
- •Апериодическое звено.
- •Правило построения логарифмической амплитудно-частотной характеристики апериодического звена.
- •Колебательное звено.
- •Характеристики колебательного звена.
- •Временные характеристики.
- •Частотные характеристики колебательного звена.
- •Логарифмическая амплитудно-частотная и фазо-частотная характеристики колебательного звена.
- •Дифференцирующее звено первого порядка.
- •Характеристики дифференцирующего звена первого порядка.
- •Временные характеристики.
- •Частотные характеристики.
- •Дифференцирующее звено второго порядка. Математические модели
- •Временные характеристики:
- •Частотные характеристики:
- •Логарифмические частотные
- •Правило построения асимптотических амплитудно-частотных характеристик разомкнутых систем автоматического управления.
- •Об устойчивости.
- •О переходном процессе.
- •О точности системы.
- •Точность систем автоматического управления при гармоническом входном воздействии.
- •Основные виды корректирующих устройств систем автоматического управления.
- •Последовательные корректирующие устройства.
- •Введение производной от ошибки.
- •Увеличение общего коэффициента усиления разомкнутой системы.
- •Введение интеграла от сигнала ошибки системы.
- •Изодромное корректирующее устройство.
- •Параллельные корректирующие устройства.
- •Положительная жесткая обратная связь.
- •Отрицательная жесткая обратная связь.
- •Инерционная жесткая обратная связь.
- •Гибкая обратная связь.
- •Инерционная гибкая обратная связь.
- •Корректирующие устройства по внешнему воздействию. Инвариантность.
- •Корректирующее устройство по задающему воздействию.
- •Корректирующее устройство по возмущению.
- •Краткое сравнение способов коррекции систем автоматического управления при помощи последовательных и параллельных корректирующих устройств.
- •Принцип дуальности управляемости и наблюдаемости.
- •В соответствии с последними уравнениями структурная схема системы имеет вид (сравнить с исходной структурной схемой).
- •Пусть заданна передаточная функция замкнутой системы
- •Или в векторно-матричной форме записи
- •Или в векторно-матричной форме записи
- •Уравнения (7)-(8), а, следовательно, и (9),(10), имеют каноническую форму записи, каноническая форма управляемости.
- •Пример. Задана желаемая передаточная функция разомкнутой системы ,
- •Решение. Желаемая передаточная функция замкнутой системы
- •Пример. Структурная схема объекта управления имеет вид, показанный на рисунке
- •Решение. Введем обозначения
Частотные характеристики колебательного звена.
Для получения аналитических соотношений, определяющих частотные характеристики колебательного звена, надо в передаточную функцию
![]()
подставить
![]() .
В результате чего получим
.
В результате чего получим
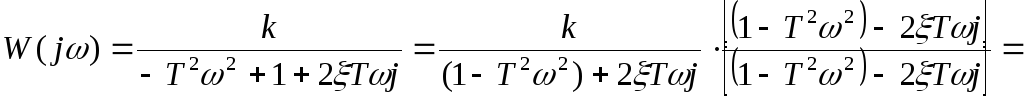
![]() .
.
Обозначим
![]() (11)
(11)
![]() (12)
(12)
Амплитудно-частотная характеристика колебательного звена.
Для аналитического получения зависимости амплитуды выходного сигнала колебательного звена от частоты – амплитудно-частотной характеристики, воспользуемся равенством:
![]()
с учётом равенств (11) и (12) получаем:
![]() (13)
(13)
Основная
особенность частотных характеристик
колебательного звена – их зависимость
от величины
![]() .
.
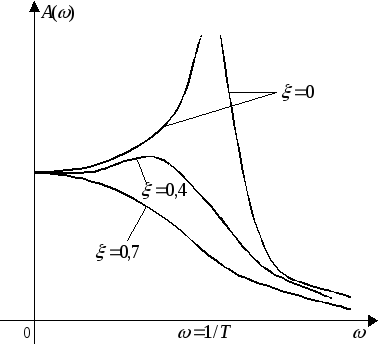
При
![]() амплитудно-частотная характеристика
колебательного звена уменьшается при
увеличении
амплитудно-частотная характеристика
колебательного звена уменьшается при
увеличении![]() ;
если
;
если![]() у амплитудно-частотной характеристики
колебательного звена появляется «горб»,
а при
у амплитудно-частотной характеристики
колебательного звена появляется «горб»,
а при![]() амплитудно-частотная характеристика
при
амплитудно-частотная характеристика
при![]() терпит разрыв.
терпит разрыв.
Фазо-частотная характеристика колебательного звена.
По определению фазо-частотная характеристика определяется как функция частоты согласно формуле:
![]() .
.
Учитывая
свойства функции
![]() из равенств (11) и (12) получаем аналитически
фазо-частотную характеристику
колебательного звена:
из равенств (11) и (12) получаем аналитически
фазо-частотную характеристику
колебательного звена:
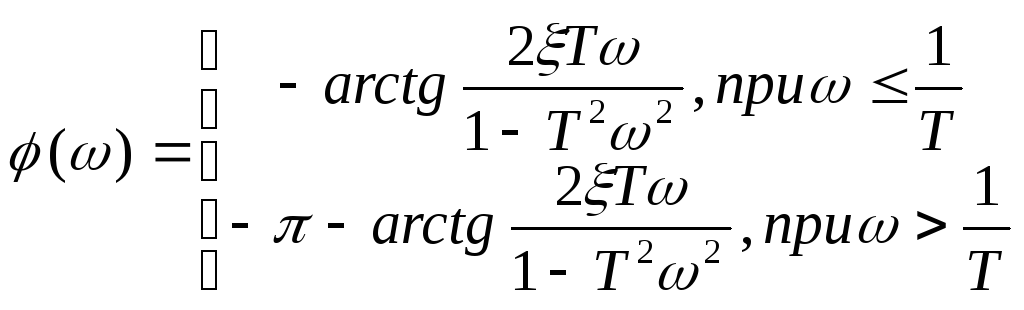 (14)
(14)
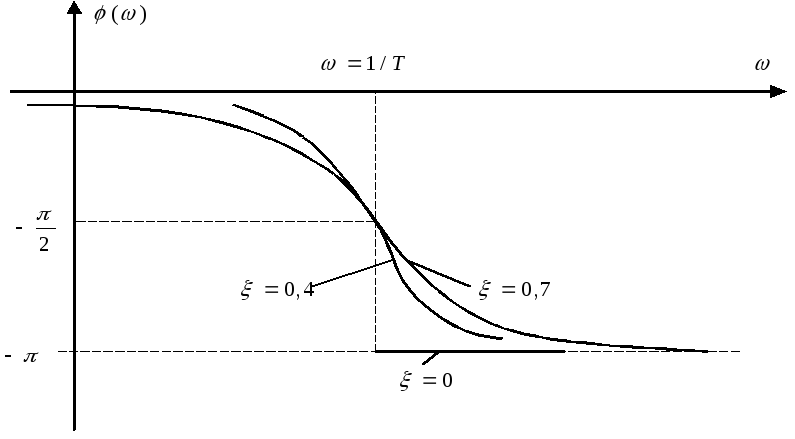
Фазо-частотная
характеристика колебательного звена
при изменении частоты от 0 до
![]() монотонно уменьшается от 0 до
монотонно уменьшается от 0 до![]() .
.
Колебательное звено создаёт отставание выходной величины тем больше, чем больше частота входного сигнала.
Амплитудно-фазо-частотная характеристика колебательного звена.

![]() -
это резонансная частота, соответствующая
максимальной амплитуде – точка
пересечения графика годографа мнимой
оси.
-
это резонансная частота, соответствующая
максимальной амплитуде – точка
пересечения графика годографа мнимой
оси.
Логарифмическая амплитудно-частотная и фазо-частотная характеристики колебательного звена.
Для построения логарифмических частотных характеристик рассмотрим
![]() .
.
С учётом уравнения для амплитудно-частотной характеристики колебательного звена (13) последнее равенство принимает вид
![]() (15)
(15)
Асимптотическая амплитудно-частотная характеристика колебательного звена определяется соотношением
![]() (16)
(16)
Последнее
равенство означает, что при изменении
частоты от 0 до 1/Т логарифмическая
амплитудно-частотная характеристика
колебательного звена параллельна сои
частот и проходит на «высоте»
![]() .
При частоте
.
При частоте![]() асимптота логарифмической
амплитудно-частотной характеристики
имеет наклон –40дБ/дек.
асимптота логарифмической
амплитудно-частотной характеристики
имеет наклон –40дБ/дек.
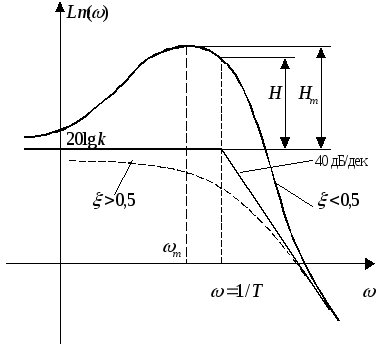
При
значениях
![]() логарифмическая амплитудно-частотная
характеристика колебательного звена
близка к асимптотической (на рисунке –
пунктирная линия).
логарифмическая амплитудно-частотная
характеристика колебательного звена
близка к асимптотической (на рисунке –
пунктирная линия).
При
значениях
![]() у логарифмической характеристики
колебательного звена получается «горб».
В этом случае необходимо вычислять
поправку
у логарифмической характеристики
колебательного звена получается «горб».
В этом случае необходимо вычислять
поправку
![]()
на частоте
![]()
Есть соответствующие шаблоны, позволяющие при построении логарифмической амплитудно-частотной характеристики колебательного звена находить соответствующие поправки.
В упрощенных расчетах достаточно использовать приближенное соотношение
![]() , при
, при ![]() .
.
Правило построения логарифмической амплитудно-частотной характеристики колебательного звена.
Отмечаем на оси частот сопрягающую частоту
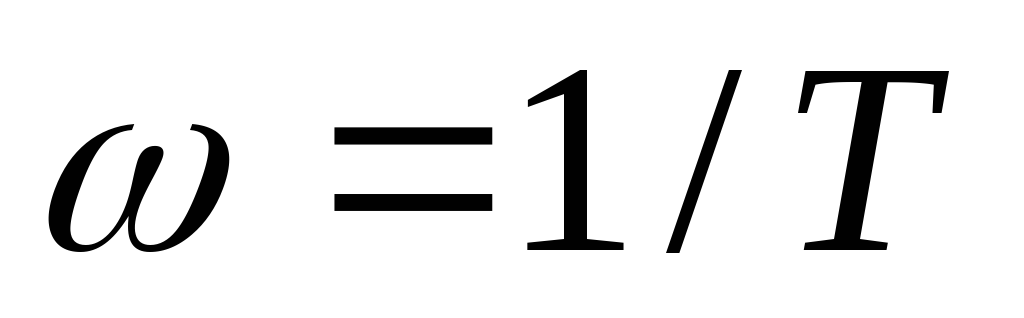 .
.На оси ординат отмечаем точку
 .
.Через точку на оси ординат, которая соответствует
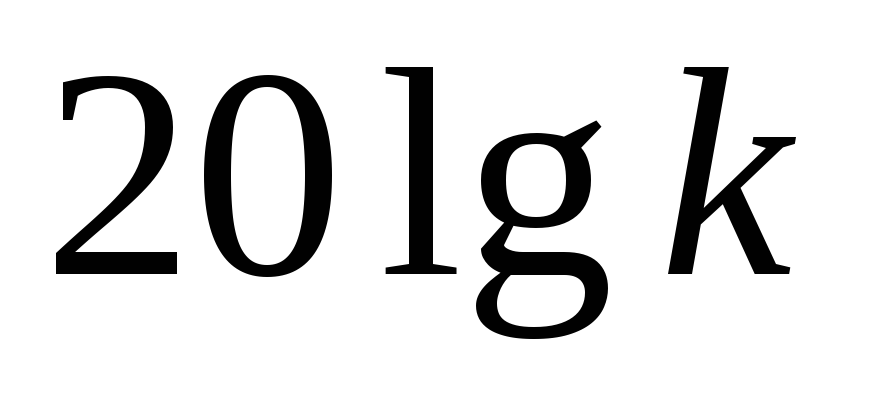 ,
проводим прямую с наклоном –40дБ/дек.
,
проводим прямую с наклоном –40дБ/дек.Через точку с координатами
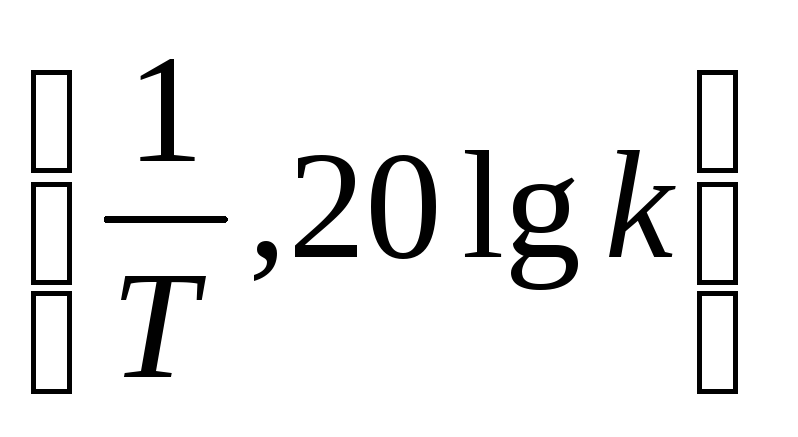 проводим прямую с наклоном –40дБ/дек.
проводим прямую с наклоном –40дБ/дек.
В результате такой последовательности действий получаем асимптотическую амплитудно-частотную характеристику колебательного звена.
Уточнить амплитудно-частотную характеристику колебательного звена, например, с помощью шаблонов в зависимости от величины
 либо с помощью формул, определяющих
величины
либо с помощью формул, определяющих
величины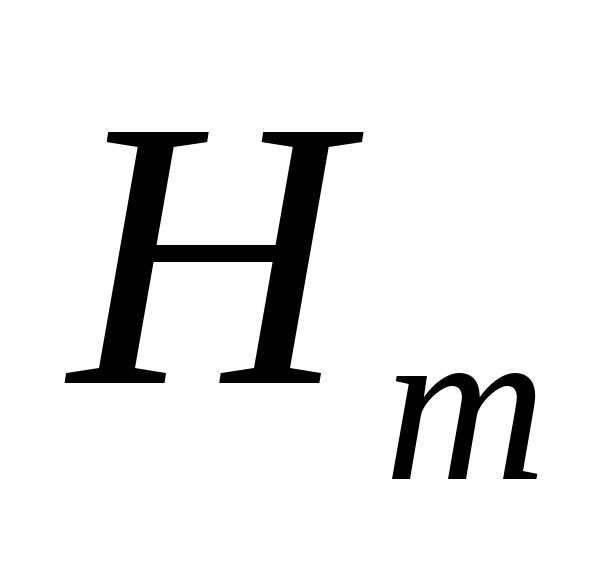 и
и как функции переменной
как функции переменной .
.
